Бесплатный фрагмент - Сборник задач по Комбинаторике

Введение

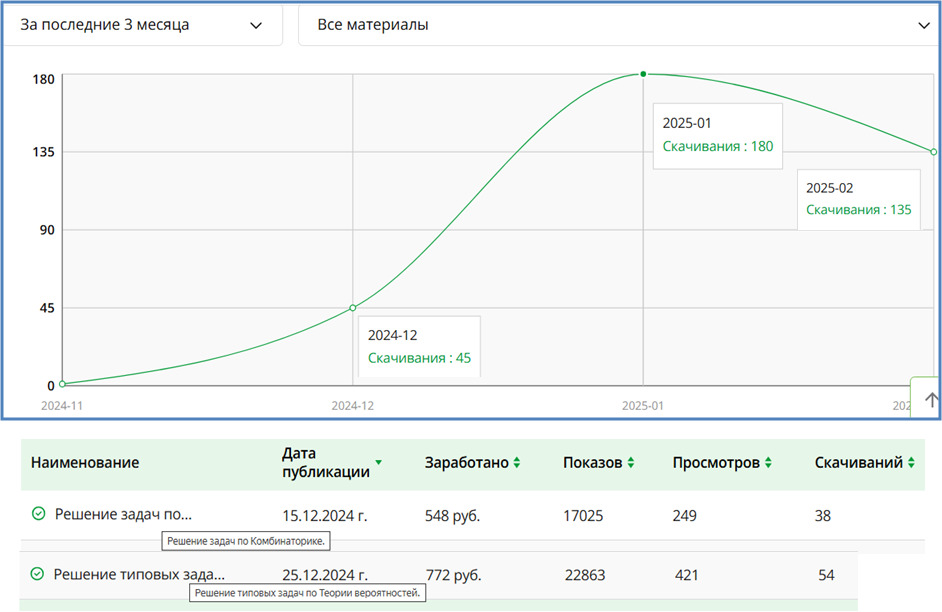
Посмотрев и оценив статистику продаж моих учебно-методических материалов на сайте Инфоурок за последние три месяца (смотрите График и легенду «популярности» моих методических разработок (МР) по Теории вероятностей на портале «Инфоурок»), я пришел к выводу, что имею полное право начинать создавать серию (ленту) электронных книг «Вероятность и Статистика».

1.1. Основные понятия Комбинаторики

Комбинаторика — это раздел математике, изучающий способы формирования и выбора конечных множеств объектов. Основные понятия включают:

— Множества: Совокупности объектов, которые могут быть определены и изучены. Объекты, являющиеся элементами множества, называются «элементами».

— Перестановки: Различные упорядоченные последовательности элементов множества. Перестановки можно рассматривать как требования к расположению объектов в определенном порядке.

— Сочетания: Подмножества, формируемые из заданного множества без учета порядка. Например, выбор двух элементов из четырех без учета их расположения.

— Разбиения: Способы разделения множества на непересекающиеся подмножества.

Размещениями называются выборки из n элементов по m элементов, комбинации, содержащие m элементов из данных n, отличающиеся составом или порядком элементов.

Перестановками n элементов называются комбинации, состоящие из всех n элементов, отличающиеся порядком элементов.

Сочетаниями по m элементов из данных n элементов называются комбинации, содержащие m элементов и отличающиеся их составом. A_ {mn} = C_ {mn} *P_m; C_ {mn} = n (n-1) (n-m+1) /m!.

1.2. Перестановки

Перестановки могут быть классифицированы по:

— числу перестановок: Для множества из n элементов количество перестановок равно n = n! (n факториал). Например, для 3 элементов: 3! = 6.

— различным перестановкам с пробелами: Когда в перестановке учитываются некоторые элементы (например, пробелы), используются формулы с делением на факториалы для учета повторяющихся элементов. Например, для множества из n объектов, содержащего k одинаковых элементов, число перестановок рассчитывается как n!/k!.

Задачи на подсчет числа перестановок

1. Найти количество способов расставить n книг на полке.

2. Определить, сколькими различными способами можно задать участие в соревновании.

Задачи на количество различных перестановок с пробелами

1. Рассчитать число способов размещения n объектов с k пробелами между ними.

2. Узнать количество различных упорядоченных последовательностей, в которых некоторые элементы повторяются.

1.3. Сочетания

Сочетания можно делить на:

— Сочетания без повторений: Определяется как количество способов выбрать k элементов из n без учета порядка. Формула: C (n, k) = n!/k! (n-k)!.

— Сочетания с повторениями: Число способов выбрать $k$ элементов из $n$ с учетом повторений. Формула: C (n+k-1, k).

Задачи на выбор подмножеств

1. Выбрать k студентов из группы с n студентами.

2. Определить, сколько различных наборов фруктов можно выбрать, если некоторые фрукты могут повторяться.

1.4. Принципы счёта

Комбинаторика использует несколько принципов подсчета:

— Принцип умножения: Если существует m способов выполнить одно действие и n способов выполнить другое, то общее число способов выполнить оба действия равно m x n.

— Принцип сложения: Если одно из двух действий можно выполнить двумя различными способами, то общее число способов выполнения одного из этих действий равно сумме количества способов выполнения каждого из них.

— Принцип включения-исключения: Используется для подсчета количества элементов в объединении нескольких множеств, позволяя избежать двойного счета.

Задачи на применение принципов

1. Определить общее количество способов составить меню из нескольких блюд.

2. Найти общее число маршрутов из одного города в другой с учетом различных транспортных средств.

1.5. Разбиения

Разбиение множества заключается в разделении его на подмножества так, чтобы каждое подмножество не пересекалось и охватывало все элементы оригинального множества.

Задачи на разбиение множества на подмножества

1. Разделить группу людей на команды.

2. Определить способы разбиения множества задач на подгруппы для выполнения.

1.6. Рекуррентные соотношения

Рекуррентные соотношения используются для решения комбинаторных задач, где результат зависит от предыдущих значений.

Решение задач с использованием рекуррентных соотношений

1. Подсчет количества способов разложить n элементов с использованием предыдущих значений.

2. Решение задач c последовательностью Фибоначи, где каждый элемент зависит от двух предыдущих.

Комбинаторика — это мощный инструментарий в математике, который позволяет решать множество практических задач через различные подходы к подсчету.

1.Решение задач традиционными методами

Задача 1

Сколько можно составить телефонных номеров из 6 цифр каждый так, чтобы все цифры были различны?

Это пример задачи на размещение без повторений.

Размещаются здесь 10 цифр по 6. А варианты, при которых одинаковые цифры стоят в разном порядке, считаются разными.

Если X-множество, состоящие из n элементов, m ≤ n, то размещением без повторений из n элементов множества X по m называется упорядоченное множество А, содержащее m элементов из n элементов.

Количество всех размещений из n элементов по m обозначают

n! — n-факториал (factorial анг. сомножитель) произведение чисел

натурального ряда от 1 до какого либо числа n. n!=1*2*3*…*n. 0!=1.

Значит, решение данной задачи будет следующим

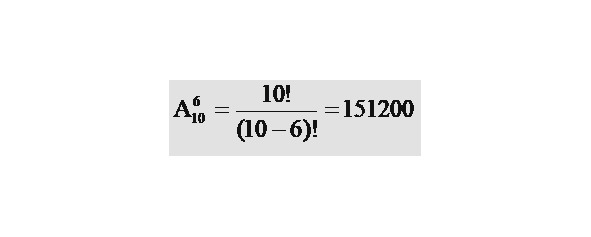
Ответ: 151200

Задача 2

У одного человека 7 книг по математике, а у второго — 9. Сколькими способами они могут обменять друг у друга две книги на две книги.

Так как порядок следования книг не имеет значения, то выбор 2 книг — сочетание. Первый человек может выбрать 2 книги 21 способом:

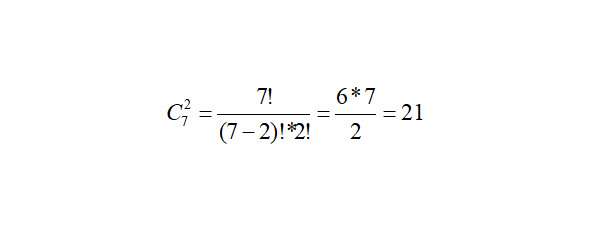
Второй человек может выбрать 2 книги 36 cпособами:

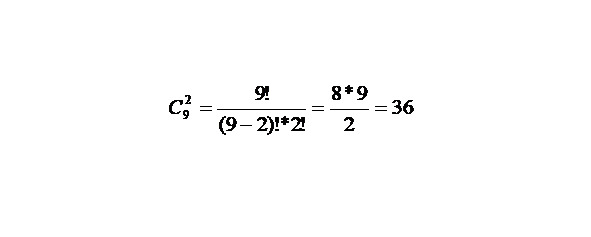
Значит всего по правилу произведения возможно 21*36=756 вариантов.

Ответ: 756

Задача 3

Студент должен выполнить практическую работу по математике. Ему предложили на выбор 17 тем по алгебре и 13 тем по геометрии. Сколькими способами он может выбрать одну тему для практической работы?

X=17, Y=13

По правилу суммы X U Y= 17+13 = 30 способов.

Ответ: 30

Задача 4

Переплетчик должен переплести 12 различных книг в красный, зеленый и коричневые переплеты. Сколькими способами он может это сделать?

Решение:

Имеется 12 книг и 3 цвета, значит по правилу произведения возможно 12х3 = 36 вариантов переплета.

Ответ: 30

Задача 5

Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?

Решение:

В таких числах последняя цифра будет такая же, как и первая, а предпоследняя — как и вторая. Третья цифра будет любой.

Это можно представить в виде XYZYX, где Y и Z -любые цифры,

а X — не ноль. Значит по правилу произведения количество цифр

одинаково читающихся как слева направо, так и справа налево равно 9*10*10 = 900 вариантов.

Задача 6