Бесплатный фрагмент - Рисунок по представлению

От автора

Настоящее пособие призвано помочь студентам художественных и архитектурных учебных заведений, а также тем, кто хочет самостоятельно овладеть техникой рисунка, ускорить усвоение учебных программ. Работа насыщена универсальным материалом, она содержит в себе подробные пошаговые уроки рисунка и другую полезную информацию. Думается, она вызовет профессиональный интерес у архитекторов, дизайнеров, художников, а также преподавателей дисциплины «Рисунок».

Столь широкий диапазон рекомендуемого внедрения обусловлен тем, что в основу работы положено построение постановок методом геометрического анализа. Или, как его еще называют — архитектурным методом, ошибочно приписываемым только архитектурной школе, правда, ею более всего распространяемым. В действительности предлагаемому методу уже более 80 лет, и настоящая работа опирается на прочный научный фундамент таких трудов выдающегося художника и педагога П. Я. Павлинова, как «Графическая грамотность» и «Каждый может научиться рисовать», продолжателей его дела — архитекторов-педагогов Тихонова С.В, Демьянова В. Г., Подрезкова В. Б. (учебник «Рисунок». М. 1983 г.) и ряда других.

Аналитический подход, давно доказавший свою высокую эффективность в освоении предмета, который П.Я.Павлинов называл объективным, описательно-показательным, стоит в оппозиции к подходу, обычно практикуемому художественными школами и училищами — его сторонники призывают всецело довериться натуре и интуиции, по сути не анализируя изображаемое, а «выражая» с позиций субъективного восприятия. В эпиграфе книги «Каждый может научиться рисовать» автор привел слова французского философа Д. Дидро (1713—1784): «Страна, в которой учили бы рисовать так же, как учат читать и писать, превзошла бы все остальные страны во всех искусствах, науках и мастерствах». А сам Павлинов отмечал, что не каждый рисующий человек может стать художником, как и не всякий владеющий грамотой — стать писателем, но пояснить мысль посредством рисунка «должен уметь и инженер, и педагог, и научный работник».

Однако сопротивление архитектурному методу выразилось не в нежелании людей приобщаться к «прекрасному» как таковому, его встретили именно предлагаемые пути овладения предметом. Иначе говоря, наблюдаемая конфронтационная позиция многих школ «нейтрализует» естественную тягу учащихся к овладению более эффективными методами познания мира, единым языком, известным с давних времен, но преподносимым многими педагогами как малоэффективный.

Геометрический анализ в учебном довузовском рисунке является главным инструментом в формировании у учащегося объемно-пространственного мышления. Такой подход ставит своей целью за полгода-год не только объяснить основы рисунка, но научить мыслить «комплексно», подразумевая под этим умение сопоставлять перспективные виды, наблюдаемые в натуре, с ортогональными проекциями, дающими объективное полное о них представление. А ведь такой рисунок будет не только красив, выразителен, но и точен, а значит всесторонне полезен.

Стандартный курс изучения рисунка в архитектурных классах, благодаря которым и был во многом распространен сам аналитический (геометрический, объективный) подход в рисовании, начинается с таких упражнений, как изображение кубов в пространстве («перспективы»), несложных и сложных врезок (например, куб, врезанный в куб; шар, врезанный в призму с некоторым смещением шара по одной из координат), и заканчивается такими заданиями, как голова, интерьер, экстерьер (городской пейзаж).

Курс архитектурного рисунка делит на два условных этапа задание «объемная композиция из геометрических тел», являющееся предметом рассмотрения данной работы. Первый этап ставит своей задачей научить абитуриента воспринимать окружающее как совокупность пространственных геометрических объемов и аналитически работать с ними. Второй этап — научить пользоваться полученными на первом этапе знаниями. Второй этап является логичным продолжением первого; лучше всего это можно проследить в таких постановках, как натюрморт с включением геометрических тел, непосредственно в постановке архитектурной детали (розетка, ионик, ваза, капитель), интерьере и завершающем курс городском пейзаже. Рисование обязательных в художественных и архитектурных вузах постановок — головы, фигуры — также не является оторванным от общего процесса познания мира через геометрических анализ, и также «проверяется», строится, как и при работе с любой геометрической формой.

Наше пособие в основном будет посвящено первому этапу. Определенная отрешенность от натуры, оторванность от функции, от назначения предмета исследования, от «первого впечатления» — позволяет рисующим более осознанно выполнять работу и, как следствие, более эффективно создавать образ, который всегда индивидуален.

Глава 1. Проблемы проверки и самопроверки учебного упражнения «Композиция из геометрических тел»

Перед преподавателем художественной школы, колледжа, вуза часто встает вопрос — какой рисунок считать наиболее достоверным. Когда работа идет с натурой, ответ кажется очевидным. Тогда как в рисовании по представлению ответ дать не только сложно, но и сама постановка вопроса кажется лишенной смысла. Любой рисунок может быть «красивым по-своему», и все зависит только от того, кто его оценивает. На сегодняшний момент нет никаких общепринятых или, по крайней мере, общеизвестных правил, чтобы оценить работу по объективным критериям, наличию и отсутствию ошибок. Все на первый взгляд ошибки, или наоборот, преимущества являются вкусовыми, именно общепринятыми, но часто спорными, а порой просто вредными для самого процесса — когда очевидные ошибки построения компенсируется внешним прилежным видом рисунка. Это поставило перед педагогами задачу — сформулировать критерии оценки. Такие часто фигурирующие в оценках «ошибки», как «кривые линии», «небрежность», «невнимательное отношение к работе», выглядят особенно неубедительно, когда речь идет о серьезном экзаменационном испытании, от которого зависит зачастую профессия испытуемого.

Первые попытки сформулировать общие правила в построении геометрических тел привели к еще большим «разночтениям» ввиду того, что они не были сформулированы до конца и носили характер скорее рекомендательный. Оправданием таких «сырых» методик было то, что рисунок не является областью начертательной геометрии. Это справедливо отчасти; основа рисунка, его «главная формула», о которой будет сказано ниже, в третьей главе, не является обязательной в построении и проверке, например, в начертательной геометрии; но в основе своей, когда речь заходит о самопроверке или когда встает необходимость добиться наибольшей точности изображаемой постановки, неизбежно требует знания именно в этой области.

Но такие инструменты, как построенная линия горизонта, использование прототипов геометрических тел в натуре, переходные упражнения вроде натюрморта, интерьера, экстерьера, отдельные специальные семинары, разъясняющие основы перспективного изображения, чаще не дают необходимого эффекта. Работа обязана быть не только «достоверной» в «видимой» части, не только убедительной с первого взгляда, к чему, как предполагает стандартная методика, ученик приходит с опытом, но и быть точной, полезной для освоения смежных, сопрягаемых курсов, таких как промышленное и архитектурное проектирование, черчение, бумажное моделирование, дизайн и т. п.

Иными словами, нынешний композиционный рисунок даже в ведущих профильных вузах представляет собой довольно сложную геометрическую конструкцию, не лишенную часто и сложного авторского сюжета — то есть одной из целей самого упражнения, но не имеет под собой базы, основанной на реальном представлении о пространстве. Следовательно, все «надстройки» в виде внедрения нестандартных геометрических фигур непосредственно в само условие задания «сложных» сечений — бессмысленны, пока не сформулирован ответ на ключевой вопрос — что может отвечать за точность и «достоверность» в пространстве плоскости, фигуры, тела. А отсюда: точность размеров, пропорций, перспективы и, в конечном счете, убедительность общего впечатления от работы.

В практике при анализе и проверке работы применяется квадрат с вписанной в него окружностью: квадрат помогает оценить глубину, также модульный квадрат помогает определить пропорции фигур, а окружность «помогает» самому квадрату быть достоверным. Казалось бы, эти два взаимосвязанных приема вполне могут сформировать должный рисунок, но положение осложняется тем, что трехмерное пространство не обеспечивает той свободы, которая возможна в изображении двухмерного пространства. Трехмерное пространство требует конкретных знаний. Например, нарушение последовательности выполнения рисования квадрата куба, когда эллипс вписывается в квадрат, а не наоборот, ведет к тому, что «ожидаемая» окружность оказывается «в плане» овалом, а не окружностью, вытянутой по ширине или высоте. Эта ошибка легко выявляется посредством построения боковых и верхних проекций. Ошибка возникает вследствие «случайного» поворота оси эллипса, вписанного в квадрат, расположенного на предметной плоскости, Такой квадрат, как и всю композицию в целом, всегда проще начать заново, чем пытаться исправить в ней первую, фундаментальную ошибку. Иными словами, если квадрат не является квадратом, тогда вне всяких сомнений куб не будет кубом, а отсюда призма призмой, пирамида пирамидой, и количество ошибок будет равняться количеству геометрических тел.

И это лишь один пример того, с чем приходится сталкиваться учащемуся в освоении рисунка, дисциплины, казалось бы, далеко не самой сложной. А ведь из вольной трактовки формы прямиком вытекают не менее существенные проблемы, с которыми преподавателю рисунка приходится иметь дело, косвенно свидетельствующие о незнании предмета как объекта комплекса характеристик пространства и объема. Приведем лишь некоторые наиболее распространенные ошибки, возникающие порой даже в работах, оцененных как хорошие и очень хорошие:

1. «Случайные врезки», когда геометрические тела «накладываются» на предыдущие тела без привязки к ним, то есть тело врезается в предыдущее сформированное тело посредством наложения силуэта тела, а не строится из узловых точек, сечений. У этой проблемы несколько причин. Чаще всего это нежелание или неумение работать с ортогональными проекциями, с тем, что архитекторы называют планами и фасадами. А отсюда вытекают ошибки как пропорциональные, так и ошибки непосредственно в сечениях, не говоря уже о том, что таким образом само название экзаменационного или курсового упражнения — композиция — теряет смысл.

2. Отсутствие ортогональных проекций в процессе создания композиции. Это не является ошибкой как таковой, но косвенно свидетельствует о том, что у учащихся не сформировано цельное представление об изображаемых предметах. Печально, что такой подход скорее поощряется в ряде вузов, считается, что студент, способный справиться без вспомогательных зарисовок, будь то эскизы, вынесенные за рамки листа сечения, или непосредственно ортогональные проекции — обладатель выработанного архитектурного чутья. Более того, вместо конкретных практических упражнений, способных расширить «пространственный кругозор», часто ограничиваются беседами о ритме, гармонии масс, масштабе и метре. Это по сути совершенно справедливо, но ведь при таком подходе именно гармонии и в отдельности ритма лишается композиция.

Без параллельного контроля через вспомогательные рисунки мы имеем дело с наслаиванием тел друг на друга, с такой же последующей врезкой тел «куда придется». Именно понимание, как будет формироваться тело, как оно выглядит в различных ортогональных проекциях, из каких конкретных точек и линий оно поднимется или опустится, и насколько именно, от плоскости тела уже сформированного, и обеспечивает осмысленность в работе, некоторый гармоничный сюжет, искомый ритм.

3. Непонимание законов линейной перспективы. Увы, и здесь мы вынуждены констатировать, что линейная перспектива часто преподносится учащимся как рекомендация, чтобы получилось «ровней», «убедительней». Предлагаются абстрактные точки схода, условная линия горизонта, в то же время в современных методиках отсутствуют ортогональные проекции предлагаемых трехмерных сюжетов. Это не означает, что в работе надо искать все перечисленное, но понимание правил перспективы исключает существенную долю ошибок, связанных с искажением изображаемых предметов. Однако учащимся предлагаются термины, предлагаются некоторые схемы из курса начертательной геометрии, но бессистемно, когда не указывается на взаимосвязь плана, фасада и непосредственно перспективного изображения.

4. Неумение сопоставить перспективный вид с планом и боковыми проекциями приводит к непониманию и «природы» эллипса, а такая тема, как «Раскрытие эллипса и квадрата», часто ставит даже опытных рисовальщиков в тупик. В различных методиках нередко встречаются практические советы, как изобразить эллипс наиболее убедительно, например, даже при помощи двух кнопок и бечевки, но нет таких упражнений, которые бы связали ортогональную проекцию эллипса (то есть окружность или линию) с перспективным изображением. Отсюда у учащихся, с одной стороны, нередко наблюдается зацикленность на некотором образе «правильного» аккуратного эллипса с определенным раскрытием, всегда примерно одинаковым, а с другой стороны, наблюдается оторванность эллипса от квадрата, как понятия как бы параллельного, никак с ним не связанного. Это, очевидно, не только не дает сориентироваться в изображаемом пространстве, но и формирует вредный стереотип, когда конкретному телу назначается отдельный алгоритм построения. Тогда как в ортогональной проекции то или иное разбираемое геометрическое тело будет представлять собой тот или иной геометрический примитив: окружность, квадрат, треугольник, причем эти же фигуры — треугольники, круги легко впишутся в квадрат или в прямоугольник.

Вышеизложенные системные ошибки подтверждают необходимость создания пошаговых, доступно изложенных пособий по самостоятельному освоению таких упражнений, как натюрморт и композиция из геометрических тел.

Глава 2. Перспектива

Общие положения

Перспектива (фр. perspective от лат. perspicere — смотреть сквозь) — техника изображения пространственных объектов в соответствии с искажением пропорций и формы изображаемых тел при их визуальном восприятии.

Перспектива, как техника изображения, появилась еще в эпоху Ренессанса, однако некоторые исследователи отмечают, что привычная современным людям прямая линейная перспектива — это плод длительного развития человеческого разума, что детям и представителям некоторых племен, например, понятнее аксонометрия и даже обратная перспектива.

Виды перспективы

Линейная перспектива. Вид перспективы с неподвижной точкой зрения, предполагающий точки схода на линии горизонта. При такой перспективе предметы в визуальном восприятии уменьшаются пропорционально по мере удаления их от зрителя. Теория линейной перспективы впервые появилась в 14 веке и до сегодняшнего дня признается как наиболее достоверное отражение мира в картинной плоскости. Разновидности линейной — угловая и фронтальная перспектива.

Обратная линейная перспектива. Вид перспективы, применявшийся в основном в византийской и древнерусской живописи. При изображении в обратной перспективе предметы увеличиваются при их удалении от зрителя, таким образом, точка схода линий находится не на линии горизонта, а как бы внутри самого зрителя. Применение этого вида перспективы было, очевидно, связано с особенностями мировосприятия православных художников-иконописцев.

Панорамная перспектива. Перспектива, строящаяся на виртуальной внутренней цилиндрической поверхности. При таком изображении точка зрения располагается на «оси цилиндра», а линия горизонта — на окружности, находящейся на высоте глаз зрителя.

Сферическая перспектива. Сферические искажения можно наблюдать на сферических зеркальных поверхностях. При изображении предметов в такой перспективе все линии глубины будут иметь одну точку схода и будут оставаться строго прямыми. Также строго прямыми будут главная вертикаль и линия горизонта. Все остальные линии будут по мере удаления от точки схода изгибаться, постепенно трансформируясь в окружность. Применялось, в частности, К. Петровом-Водкиным.

Помимо перечисленных видов, следует упомянуть воздушную перспективу, о которой речь зайдет в пятой главе — «Светотеневые отношения в рисунке»; следует также заметить, что человеку при изучении окружающей его среды свойственна так называемая перцептивная перспектива (перцепция — непосредственное восприятие). Ее свойство в том, что ближний план воспринимается человеком в обратной перспективе, неглубокий дальний — в аксонометрической проекции, дальний план — в прямой линейной перспективе. Эту воспринимаемую совокупность и принято называть перцептивной перспективой.

Однако при изучении основ рисунка достаточно одной — линейной перспективы, и далее разбираемые примеры будут рассмотрены только с ее применением.

Упражнение 1. Кубы в пространстве

Мало поставить куб и попросить учащихся изобразить его. Чаще всего такое «лобовое» задание приводит к пропорциональным и перспективным ошибкам, среди которых наиболее известны: обратная перспектива, частичное замещение угловой перспективы фронтальной, то есть подмена перспективного изображения аксонометрическим. Не вызывает никаких сомнений, что эти ошибки вызваны непониманием законов перспективы. Знание перспективы помогает не только предостеречь от грубых ошибок на самых первых этапах построения формы, но и стимулирует учащегося анализировать свою работу.

Следует отметить, что в настоящем пособии, нацеленном в том числе на самостоятельное ознакомление с основами рисования, не будут рассматриваться такие темы, поднимаемые почти каждым учебником рисунка, как «Организация рабочего места», «Разновидности красок, карандашей и ластиков» и проч. Однако важно знать, что рисунок всегда начинается с линий и точек, что он требует работы с инструментом и материалом. Потому раздел «Рекомендуемые упражнения» главы «Светотеневые отношения в рисунке» посвящен характеру линий и имеет практические рекомендации по их исполнению.

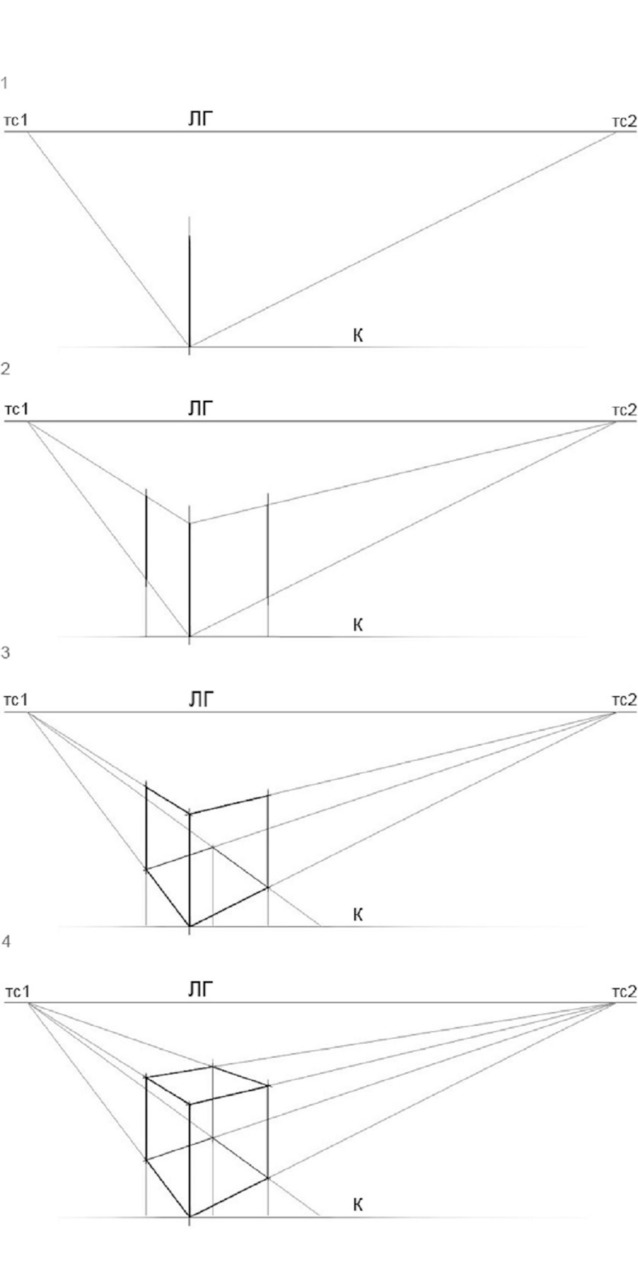
Разделите лист бумаги горизонтальной линией — таким образом вы получите линию горизонта (ЛГ). Слева и справа на ней поставьте две точки. Левая будет точкой схода «1», а правая точкой схода «2». Сначала изобразите куб в нижней части листа, затем в верхней, следя за тем, чтобы ребра кубов (кроме вертикальных ребер) строго ориентировались в точки схода. Обратите внимание на то, что вертикальные ребра куба должны быть параллельны боковым краям листа, иначе говоря, они всегда должны оставаться вертикальными (Рис.1).

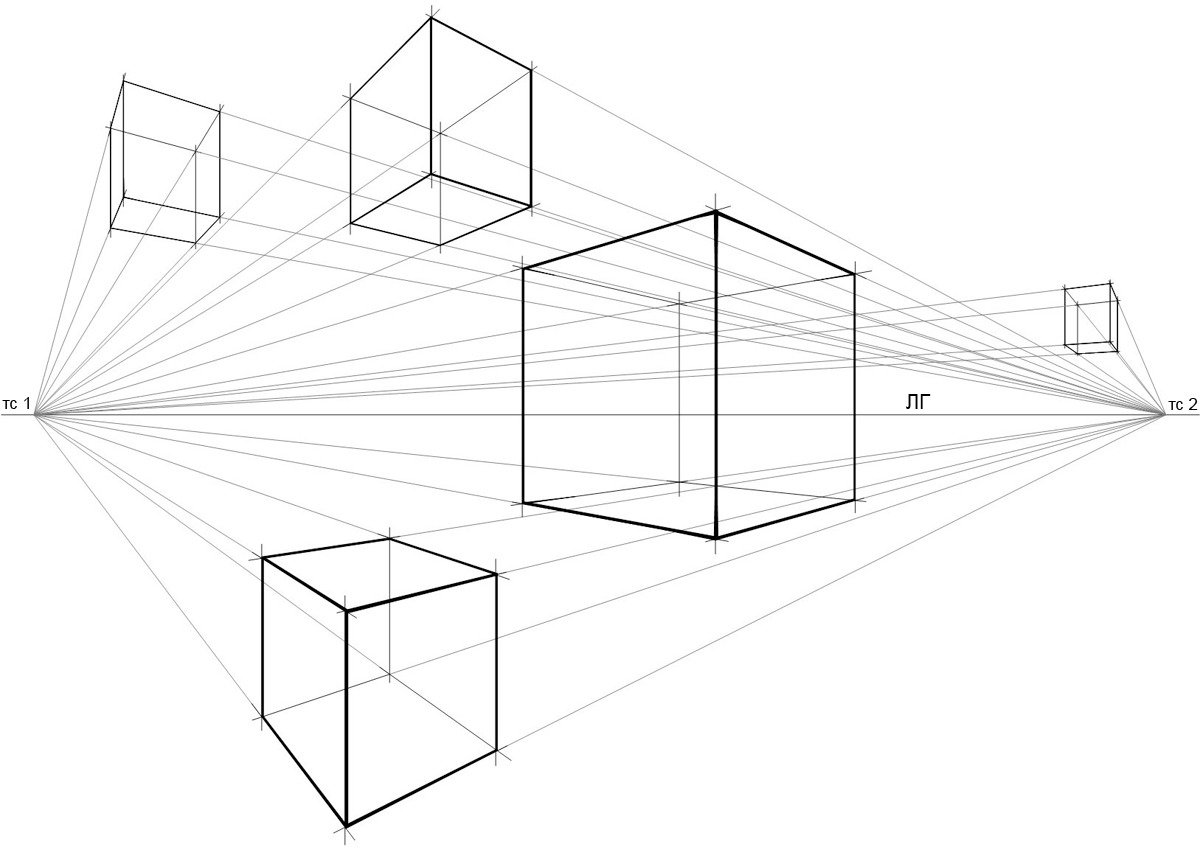
Упражнение 2. Фронтальная и угловая перспектива

К угловой перспективе следует отнести такие учебные задания, как натюрморт, как композиция из геометрических тел и многие другие. К фронтальной перспективе относятся в основном интерьеры и экстерьеры, в остальных же заданиях фронтальная перспектива встречается за редким исключением и чаще квалифицируется преподавателями как ошибка построения.

Выполнение данного упражнения не даст в будущем совершить грубые ошибки, такие, как наличие в работе обратной перспективы или перспективы угловой с частичным замещением фронтальной. Понимание, что в трехмерном изображении должно быть две точки схода, не позволяет учащемуся нарисовать ту или иную плоскость (например, сторону куба) параллельно листу.

Изобразите группу кубов, как на Рис. 2. Обратите внимание, что кубы одинаковы по размеру и находятся на одинаковом удалении от зрителя.

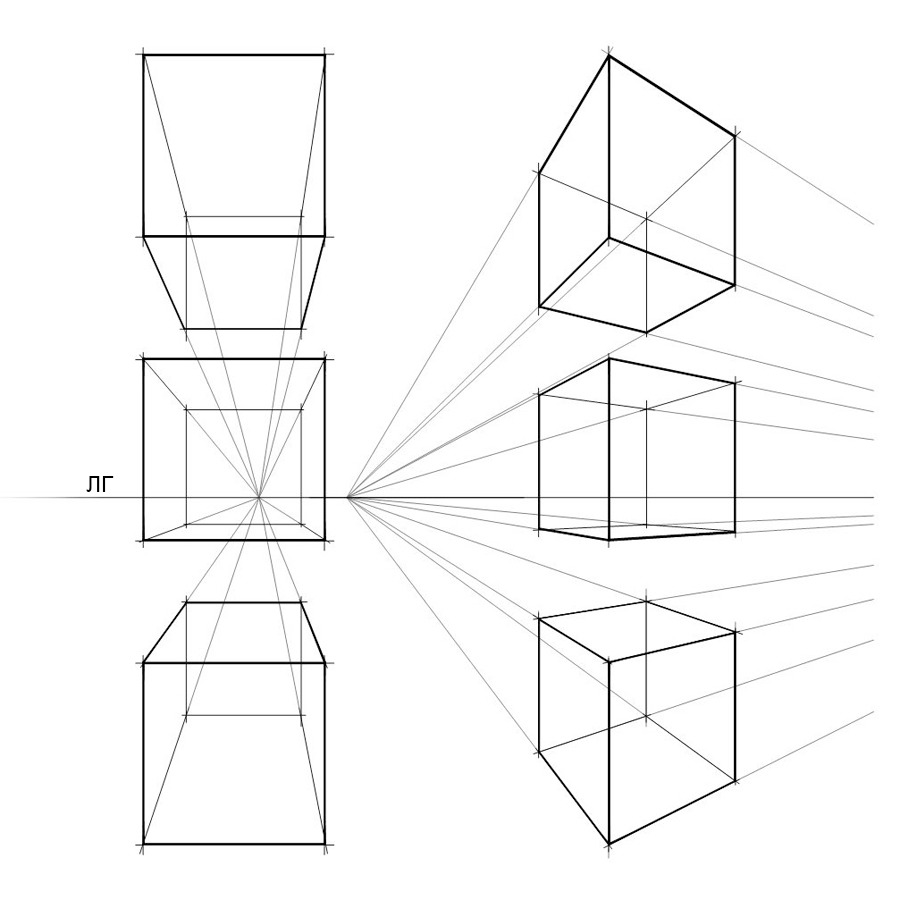
Основные термины и понятия

К — плоскость проекций (картина), преимущественно вертикальная;

Т — предметная плоскость (горизонтальная);

тс 1, тс 2 — точки схода.

S — точка зрения (центр проекций);

S1 — горизонтальная проекция точки S или план точки S;

Р — главная точка картины (ортогональная проекция точки зрения на картину);

Н — горизонтальная плоскость;

ЛГ — линия горизонта.

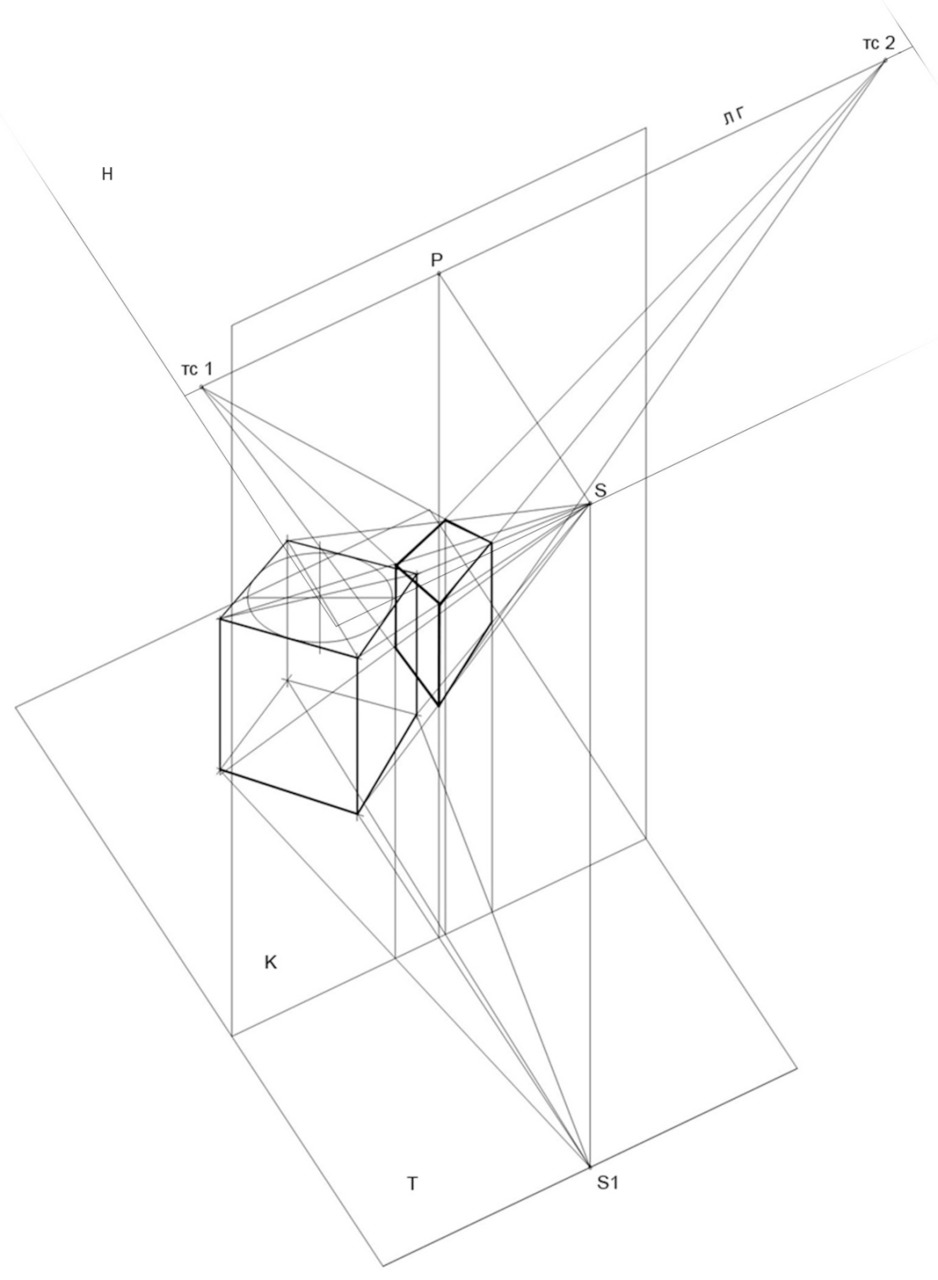
Упражнение 3. Построение куба при помощи линейной перспективы

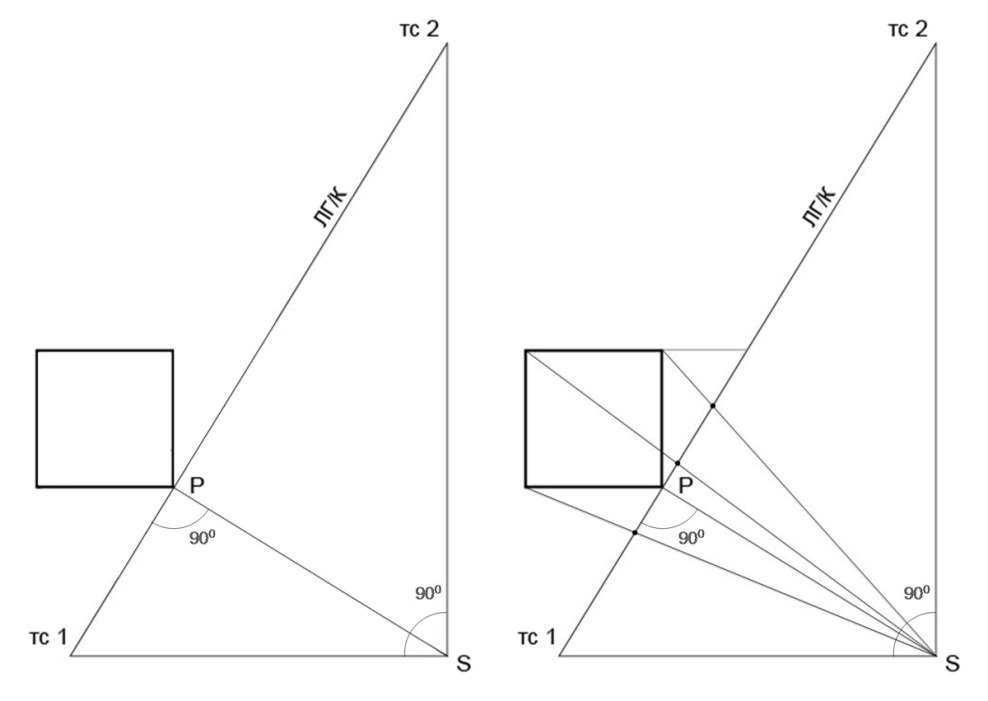
Внимательно перечертите план, показанный на Рис.4. Обратите внимание на то, что центральный луч (S-Р) перпендикулярен картинной плоскости (на плане это и линия горизонта одновременно). Отметим, что точки схода находятся на разном удалении от куба, и то, что линии, образованные точкой S и точками схода 1 и 2 перпендикулярны друг другу, и таким образом они будут параллельны сторонам квадрата.

1. Зафиксируйте расстояние от точки схода 1 до точки схода 2 на плане и перенесите его на рабочий лист, как на Рис. 5. Это будет линия горизонта, а ограничивающие этот отрезок точки — точки схода соответственно. Проведите параллельно линии горизонта линию ниже, на некотором расстоянии; чем дальше она будет отставлена от линии горизонта, тем выше соответственно будет линия горизонта по отношению к предмету — это линия будет символизировать основание картинной плоскости.

2. Теперь на плане из углов квадрата проведите линии в точку S. Точки, полученные на плане на картинной плоскости, перенесите на рабочий лист. Подняв вертикали, вы получите три ребра куба. Так как один угол куба имеет касание с картинной плоскостью, то высота его будет равняться стороне квадрата в плане.

3. Покажите в основании куба невидимые ребра, а самый дальний угол проверьте через план — найдя его посредством проведения линии в точку S из угла куба соответственно.

4. Найдите остальные ребра куба.

Попробуйте это сделать

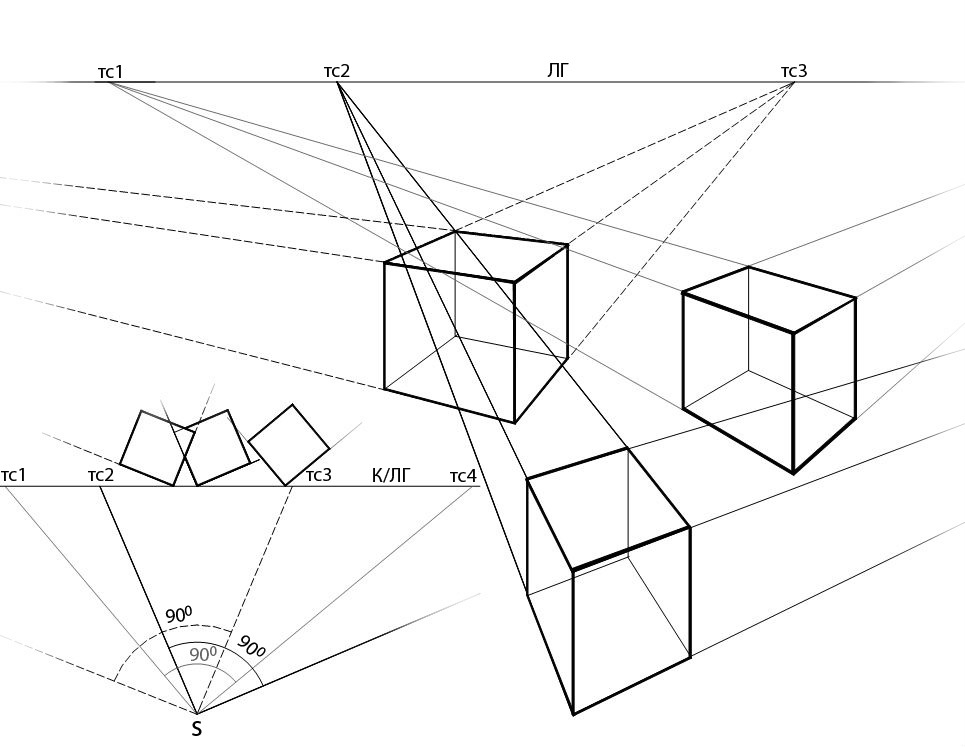
Попробуйте изобразить кубы в разных ракурсах, как на Рис. 6. Обратите внимание, что точки схода при продолжении ребер всегда будут находиться в разных местах для каждого куба, но при этом на одной линии горизонта. Из плана (в левой нижней части рисунка) видно, что кубы находятся на одинаковом удалении от зрителя, о чем свидетельствует картинная плоскость, в плане совпадающая с линией горизонта.

Отдельно, в рамках знакомства с перспективными сокращениями, следует сказать еще об одной наиболее часто встречающейся ошибке, вытекающей из вышесказанного. Это стремление учащегося совместить, в рисовании постановки с углового ракурса, дальнюю грань куба с передней. Для предотвращения этой ошибки, встречающейся зачастую даже у опытных рисовальщиков, можно провести горизонтальную линию через ближний угол квадрата основания куба (то, что в разобранных выше упражнениях называлось основанием картинной плоскости), и таким образом легко обнаружить разницу в углах — остром и менее остром, формирующих положение плоскостей куба в перспективном изображении. Наиболее острый угол свидетельствует о том, что плоскость куба, им сформированная, больше развернута к картинной плоскости, а значит и к зрителю.

Но надо сказать, что построение геометрических тел с помощью линейной перспективы дает значительные искажения, по сравнению с рисованием постановки с натуры, а если же их и не имеет, то необходимые точки для построения часто не представляется возможным найти — ввиду значительного удаления от изображаемого предмета.

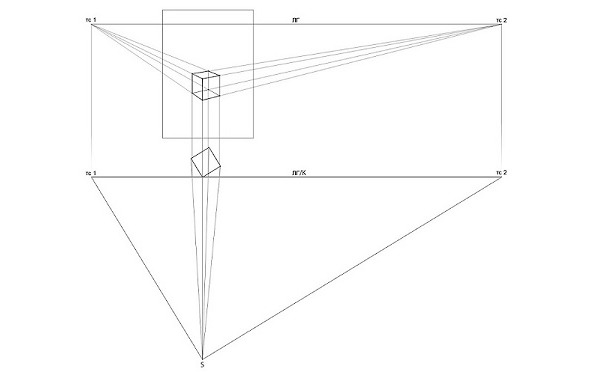
На Рис.7 показан куб, очерченный прямоугольной рамкой, имитирующей рабочий лист; это куб, который мы и будем рассматривать в дальнейшем, имея в виду точки схода, расположенные далеко за пределами листа.

Глава 3. Квадрат и куб в пространстве

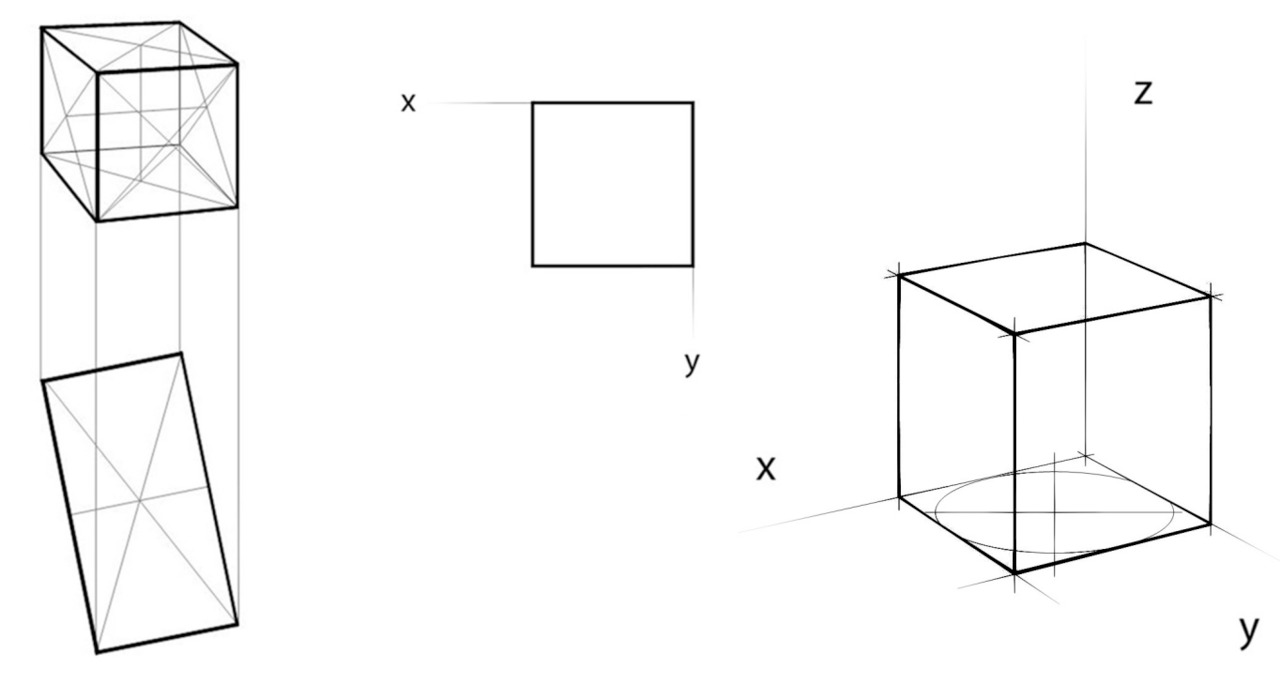
На примере геометрических тел проще всего освоить основы рисунка: перспективу, формирование объемно-пространственной конструкции предмета, закономерности светотеней. Изучение построения геометрических тел не дает возможности учащемуся отвлекаться на мелкие детали, а значит, позволяет лучше усвоить основы рисунка. Изображение объемных геометрических примитивов способствует грамотному изображению и более сложных геометрических форм. Изображать наблюдаемый предмет грамотно — это значит показывать скрытую структуру предмета. Но для того, чтобы этого добиться, существующего инструментария, даже ведущих вузов, оказывается недостаточно. В данной главе будет разобрано три упражнения, связанных с построением куба — являющимся модулем для всех геометрических тел. Так, на Рис. 8, в левой части, изображен куб, проверенный «стандартным» способом, широко распространенным в большинстве художественных школ, училищ и вузов. Однако если проверить такой куб средствами той же начертательной геометрии, представив его в плане, то выяснится, что это вовсе не куб, а есть некоторое геометрическое тело, с определенным ракурсом, наверняка и положением линии горизонта, и точек схода его только напоминающее.

К сожалению, и на сегодняшний день многие студенты даже архитектурных вузов ограничиваются лишь поверхностным представлением об изображаемых предметах, «срисовывая» только видимые пятна и силуэты с натуры, тогда как архитектор, да и художник, не только должен достаточно уверенно представлять — как изобразить предмет в отрыве от натуры, но и обязан уметь это делать. Однако многие архитекторы и художники неспособны изобразить даже группу тел по представлению, и хуже всего, что некоторые из них навязывают этот подход — «копирования с натуры» — абитуриентам и студентам. Обратимся к утверждению П. Я. Павлинова, что рисунок — наука, пускай теоретическую часть в большей мере заимствующая из начертательной геометрии и способная уместиться в небольшом количестве утверждений, но тем не менее требующая всестороннего освоения.

Так, на Рис. 8 в правой части показан куб, сориентированный по трем координатам: X,Y,Z. Такой куб может считаться модульным, так как изображен корректно, а это означает, что и рисунок с включением такого куба будет точен. Как в ортогональной проекции мы пользуемся модульным размером, например, квадратными метрами при измерении площади, так и в пространственной среде мы должны иметь точное представление о том, что такое куб и отчего зависят его ширина, глубина и высота.

Обратите внимание, что для этого вам не понадобится ни точного положения точек схода, ни точного понимания, где находится линия горизонта. Этим предлагаемый метод выгодно отличается от линейно-перспективного способа построения, разбираемого в предыдущей главе.

Упражнение 1. Построение куба

Рисунок куба следует начинать с эллипса — с окружности в пространстве; только таким образом можно избежать всех последующих ошибок, которые не имеет смысла перечислять. Ученик должен понимать, что, несмотря на всю внешнюю близость к натуре, на всю его аккуратность, рисунок, в основе которого содержится фундаментальная ошибка, неизбежно ошибочен и во всем остальном.

Иными словами, нет никакого смысла говорить о пропорциях, ритме, метре, масштабе, когда неизвестен даже размер-модуль. Этот модуль, отвечающий за все необходимые размеры: по глубине, ширине и высоте — не что иное, как куб.

Эллипс не зависит от точек схода (Рис.9), в отличие от квадрата, что дает возможность сформировать и сам квадрат, что принципиально отличает перспективу, как раздел начертательной геометрии, от рисунка. Однако есть два несущественных недочета, связанных с этим методом. Первый — исключается резкая перспектива, второй — приходится более тщательно относиться к изображению эллипса. Впрочем, первый недочет устраняется удалением точек схода от изображаемого куба, а значит, такой недочет можно рассматривать даже как преимущество, так как точки схода выходят далеко за пределы листа, поэтому исключается процедура их поиска (однако это не означает, что их не нужно предполагать). Второй недочет устраняется упражнением «Раскрытие эллипса и квадрата», которое будет рассмотрено в данной главе.

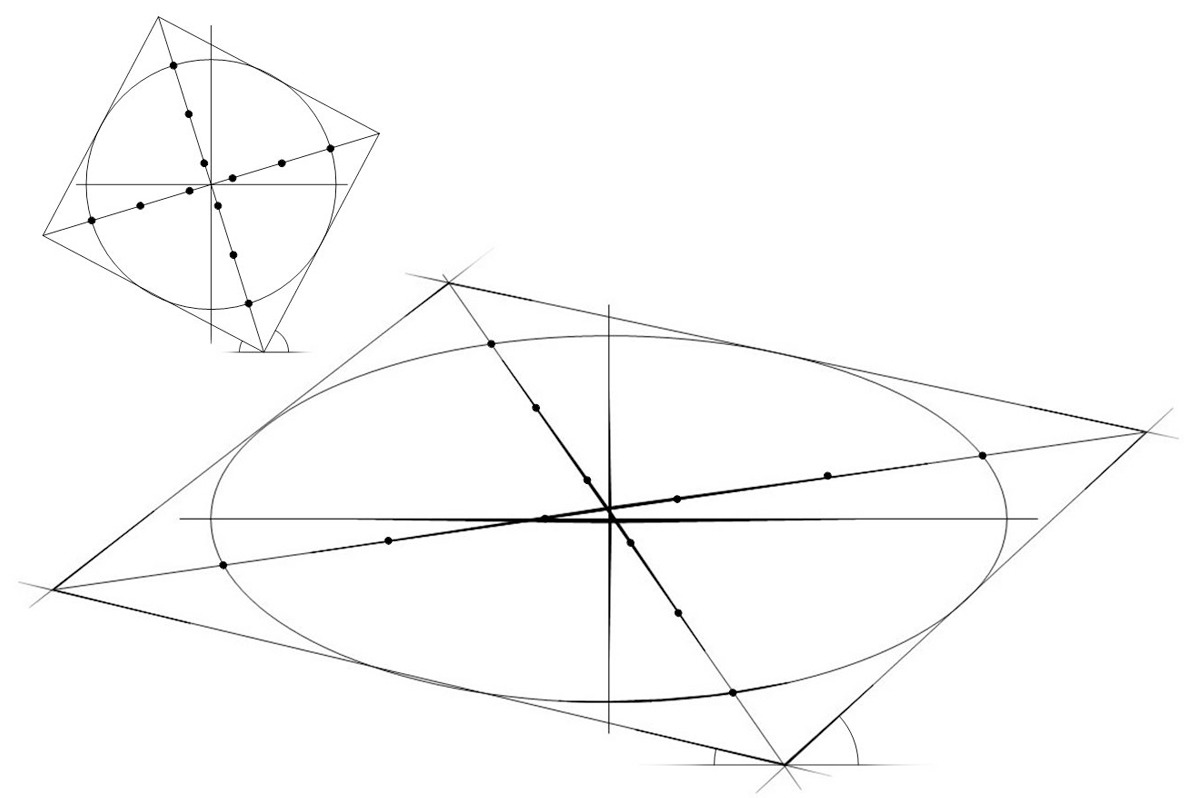
Вместе с тем этот способ позволяет буквально за считанные минуты построить не только убедительный куб с визуальной точки зрения, но и позволяет утверждать, что он изображен достоверно. Подразумевая под этим проверку линейной перспективой с незначительными погрешностями в зависимости от масштаба и непосредственно удаления точек схода. То есть чем больше будет изображаемый куб и чем дальше удалены от него точки схода — тем точнее будет попадание.

Почти любая стандартная методика по самостоятельному обучению предлагает сначала изобразить фигуру в целом. Этот подход имеет смысл только при непосредственном формировании компоновки листа, но никак не поможет в построении конкретной фигуры.

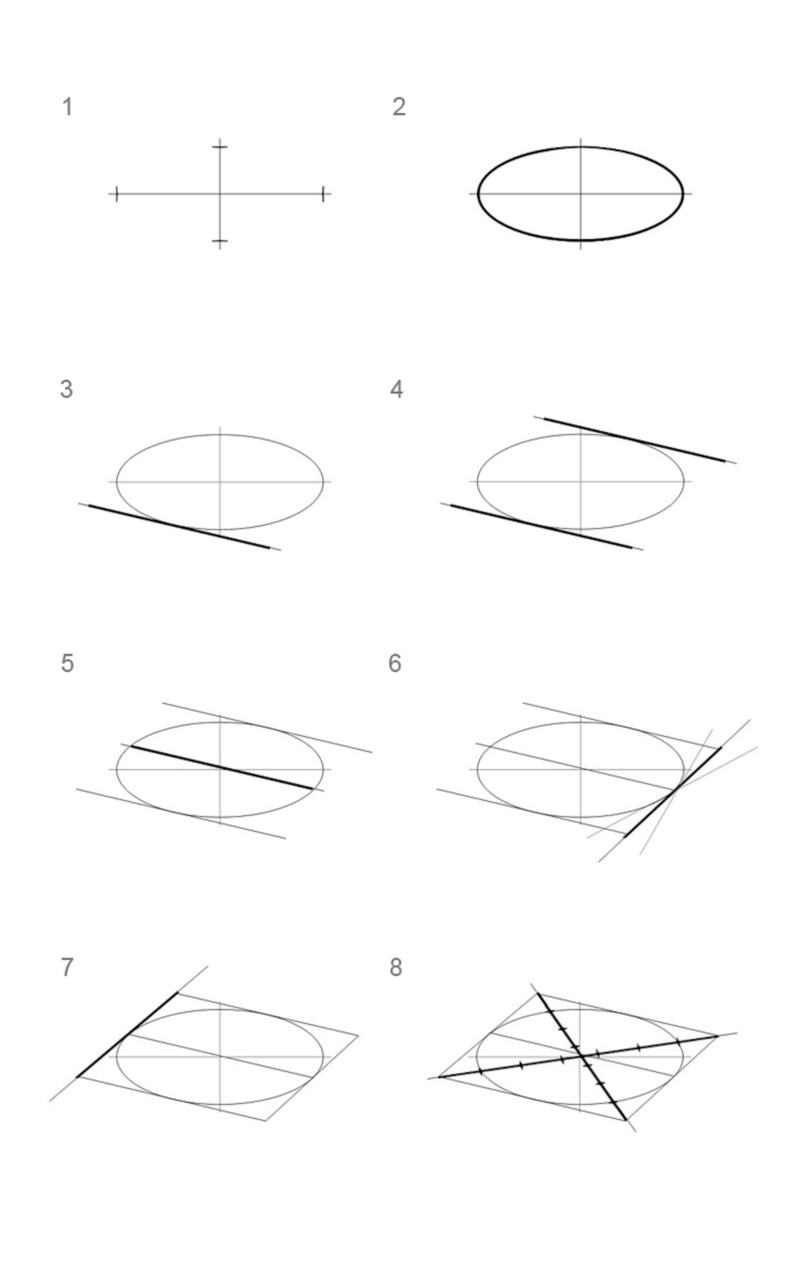
1. Проведите горизонтальную и вертикальную линии, проследив за тем, чтоб вместе они образовали прямой угол. Таким образом, вы получите большую и малую оси (Рис.10).

2. Изобразите эллипс и проверьте по точкам, расположенным по горизонтали и вертикали — они должны быть на равном удалении от центра (Рис.10).

3. Проведите произвольную прямую, получив касание с эллипсом (Рис.10).

4. Параллельно предыдущей проведите вторую прямую, с учетом незначительного перспективного сокращения — это будут будущие ребра куба (Рис.10).

5. Обратите внимание, что такой подход позволяет выбрать любое направление ребер. Проведите через центр третью линию, параллельную уже известным ребрам будущего куба (Рис.10).

6. Вспомогательная ось квадратной плоскости помогает «поставить» 3-е ребро «на свое место». Так, легкими линиями показаны еще два — неверных положения этого ребра (Рис.10).

7. Покажите четвертое ребро — параллельное ребру предыдущему. Обратите внимание, что квадрат должен искажаться, то есть он подчиняется точкам схода, тогда как эллипс не искажается. Значит, и геометрический центр квадрата не будет совпадать с центром эллипса. Однако в рассматриваемом масштабе и при таком незначительном перспективном сокращении эта разница может и не выявляться зрительно (Рис.10).

8. Как видно, такой подход позволяет избежать лишнего поиска касательных, требующего часто сложных расчетов. Проблема обнаруживается только в самом эллипсе, который, по причине рисования от руки, может иметь какие-то изъяны. Потому необходимо запомнить, что отрезок от угла куба по диагонали до пересечения с окружностью (эллипсом), должен укладываться до центра окружности примерно 2,5 раза. Это среднее значение, и ошибкой не является значение, попадающее в диапазон от 2.2 до 2.6. Число это не случайно — так, если посмотреть на изображаемый куб сверху, то есть в плане, это значение будет равняться 2.41. Очевидно и то, что чем сильнее будет раскрываться плоскость квадрата к зрителю, тем ближе это значение будет приближаться к значению в ортогональной проекции (Рис.10).

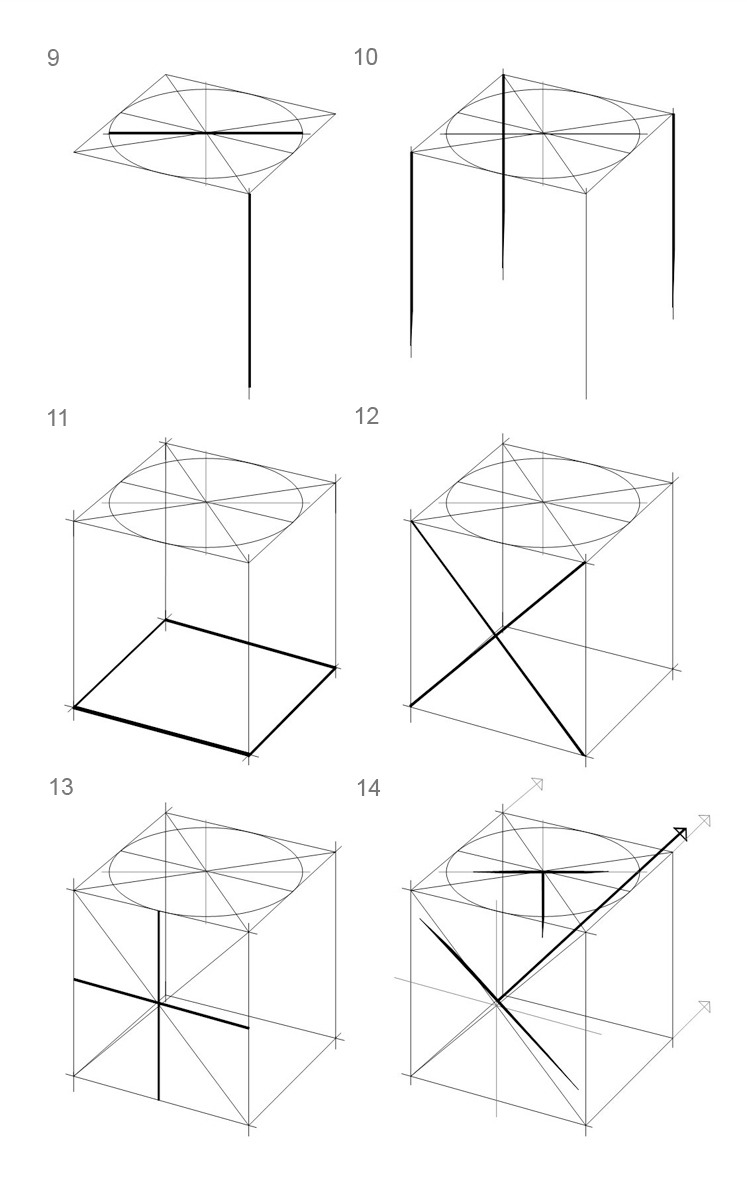
9. Большая ось эллипса характеризует натуральный размер куба, поскольку равняется высоте вертикального ребра куба, конечно, при условии незначительного перспективного сокращения (Рис.11).

10. Для дальнейшего построения куба опустите вертикали из углов найденного квадрата (Рис.11).

11. Изобразите второй квадрат с учетом незначительного перспективного сокращения (Рис.11).

12. В зависимости от масштаба и удаления точек схода от изображаемого куба, вторую горизонтальную плоскость можно проверить дополнительным эллипсом, но важнее проверить квадрат, который поможет сформировать будущие фигуры, находящиеся в вертикальном положении по отношению к предметной плоскости. Поэтому найдите геометрический центр квадрата и, значит, и эллипса (с незначительным отклонением в пределах погрешности) посредством диагоналей (Рис.11).

13. Рассеките вертикальную плоскость квадрата на две равные части по вертикали и по горизонтали (Рис.11).

14. Можно попытаться построить эллипс по четырем точкам, но следует сказать, что такое изображение эллипса будет ошибочным, если он не имеет двух проверочных осей. По аналогии с горизонтальной плоскостью квадрата, где оси, образующие прямой угол, помогали сформировать сам эллипс, следует найти необходимые оси и в плоскости вертикального квадрата. Найти вертикальную ось в данном случае поможет само положение ребер куба (это взаимное расположение и называется ракурсом). Большую же ось можно найти посредством построения прямого угла. Для чего можно использовать, скажем, угол листа бумаги (Рис.11).

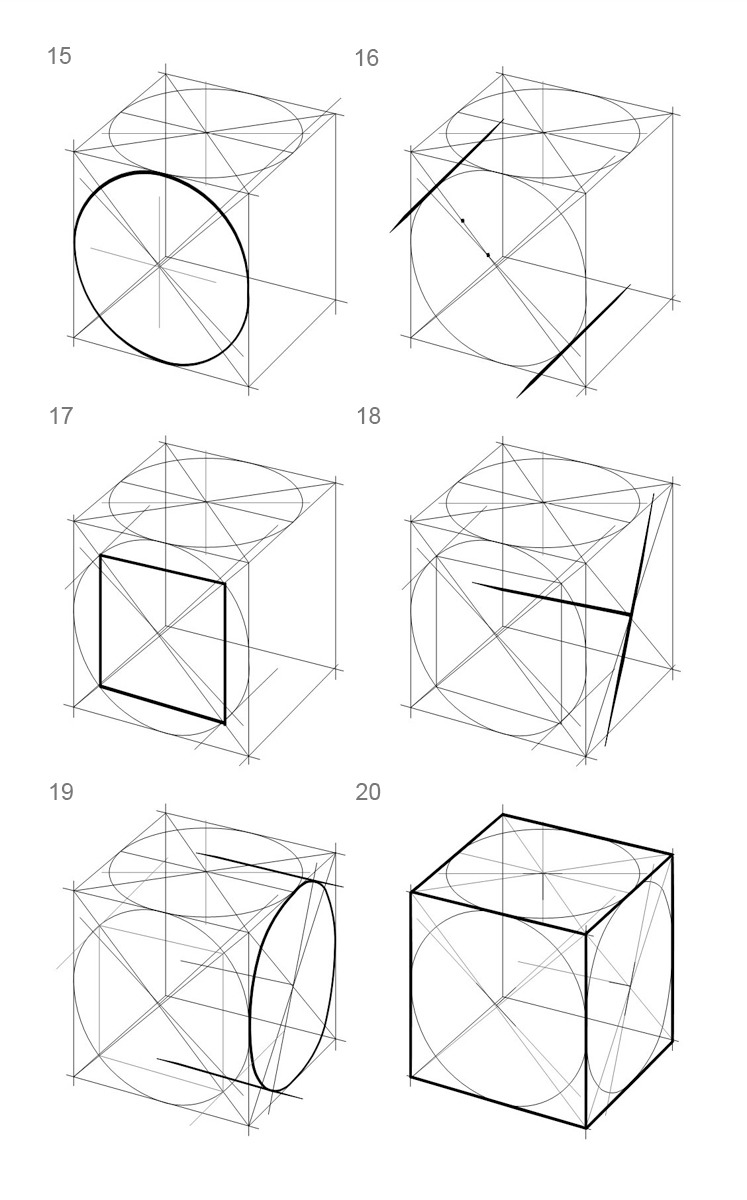
15. Впишите эллипс в вертикальный квадрат (Рис.12).

16. На рисунке показаны вспомогательные линии самопроверки — они образованы крайними точками на большой оси эллипса и самим ракурсом куба. Таким образом, если вы повернете рабочий лист так, чтоб линии горизонта соответствовала большая ось эллипса, вы убедитесь, что у вас получился достоверно изображенный фрагмент цилиндра. В этой проверке важно, чтобы точки, находящиеся на большой оси, являлись крайними по отношению к эллипсу. Они указывают, в свою очередь, на завершение формы цилиндра (Рис.12).

17. Проверьте квадрат по известной «формуле»: отрезок диагонали от угла квадрата до пересечения с окружностью должен отложиться к центру примерно 2,5 раза. Таким образом, проверив каждый угол, вы должны будете получить малый квадрат, стороны которого должны быть параллельны сторонам проверяемого квадрата куба (Рис.12).

18. Найдите оси эллипса третьего проверяемого квадрата (Рис.12).

19. Впишите эллипс в третью видимую квадратную плоскость. Проверьте эллипс (Рис.12).

20. Выделите видимые линии (Рис.12).

Проверьте себя

Имейте в виду, что принцип начисления экзаменационных баллов опирается на проверку знания предмета. На построение куба в композиции приходится основная часть проверяемых знаний и потому может состоять из нижеуказанных пунктов, а именно:

Наличие эллипса в горизонтальном квадрате модульного куба;

Наличие малой и большой осей эллипса, образующих прямой угол;

Наличие точек, указывающих на проверку эллипса, равное значению — примерно 2.5 размера отрезка по диагонали квадрата, образованного углом квадрата до пересечения с эллипсом, к центру окружности;

Высота ближайшей к зрителю вертикального ребра куба должна равняться наибольшей ширине эллипса — то есть его большой оси;

Наличие не только вписанного эллипса в одну из вертикальных плоскостей куба, но и его проверка посредством двух его осей, образующих прямой угол, и их соответствие ракурсу — положению ребер самого тела: все эти пункты следует считать обязательными, и только их отсутствие или наличие в работе может говорить более или менее точно о понимании предмета в целом. Одновременно с этим рассмотренный способ построения, в отличие от способа, опирающегося на визуальное восприятие и поиск на листе посредством силуэта общего представления об изображаемом теле, исчерпывает все существующие способы проверки. Такие, например, как метод визирования, проверку через диагонали и центры квадратов, сверку углов по картинной плоскости, иные проверки с помощью инструментов линейной перспективы, однако не дающие достаточно точного ответа на вопрос — а куб ли изображен на листе?

Упражнение 2. Вращение куба

Упражнение «вращение куба», или «ракурс куба», или то, что П.Я.Павлинов называл мультипликацией, нацелено на закрепление предыдущего упражнения — ключевого для композиции, да и рисунка в целом, построения куба.

Для выполнения упражнения полезно представить изображаемые кубы сверху и сбоку, как на Рис. 13. Алгоритм построения такой группы ничем не отличается от алгоритма построения куба в предыдущем упражнении. Ниже разбирается построение двух кубов в двух направлениях, однако их может быть и гораздо больше.

Попробуйте это сделать

Постройте сначала первый и второй куб, используя приведенные стадии построения показанные ниже (Рис.14, Рис.15), а затем и третий, как на Рис. 13 в произвольном повороте, дополнив рисунок соответствующими ортогональными проекциями.