Бесплатный фрагмент - Решаем задачи по математике

ПРЕДИСЛОВИЕ

Появление данного пособия продиктовано необходимостью помочь ученикам, готовящимся перейти из начальной школы в среднюю, овладеть методами решения наиболее сложных типов математических задач, предусмотренных школьной программой. Работа с учениками по данному пособию предполагает помощь заинтересованных родителей и доброжелательных учителей.

Замечено, что многие ученики, освоившие основной, базовый уровень, часто теряются, переходя к решению задач, рассчитанных на более свободное владение материалом школьной программы. Изложенные в пособии методы обогатят опыт ребёнка, помогут ему преодолеть неуверенность при решении сложных задач, в числе которых можно назвать задачи на движение, задачи на дроби и проценты.

Материал, приведённый в пособии, может быть использован самыми разными способами: для индивидуальной работы учеников в классе и дома, для совместной работы детей с родителями в течение учебного года или летом. Пользуясь учебными материалами пособия, родители смогут помочь своему ребёнку, не прибегая к услугам репетитора. Приступая к работе по данному пособию:

1) старайтесь добиться от ребёнка восприятия задачи как некоей жизненной ситуации, ведь каждая задача — это, прежде всего, рассказ о каких-то событиях;

2) обращайте внимание на то, чтобы перед тем как приступить к решению задачи, ребёнок внимательно прочитал и пересказал её условие (это развивает научную речь);

3) проверяйте знание ребёнком формул, используемых при решении задач (для удобства они вынесены в начало каждого раздела).

Задачи не регламентированы по времени и не рассчитаны на выполнение за один приём. Они могут обдумываться и решаться как в целом, так и фрагментарно. Каждая задача может явиться темой разговора между взрослым и ребёнком.

Дерзайте, уважаемые родители! Ваш труд и внимание к ребёнку окупятся его последующими жизненными успехами.

ЗАДАЧИ НА ДВИЖЕНИЕ

Для того чтобы найти расстояние (S), нужно скорость движения (V) умножить на время движения (t):

S = V · t

Для того чтобы найти время движения (t), нужно пройденное расстояние (S) разделить на скорость движения (V):

t = S/V

Для того чтобы найти скорость движения (V), нужно пройденное расстояние (S) разделить на время движения (t):

V = S/t

ЗАДАЧИ НА ВСТРЕЧНОЕ ДВИЖЕНИЕ

а. От двух лодочных станций, расстояние между которыми составляет 45 км, вышли одновременно навстречу друг другу две лодки. Скорость первой лодки равна 7 км/ч, скорость второй — 8 км/ч. Найдите время, через которое лодки встретятся.

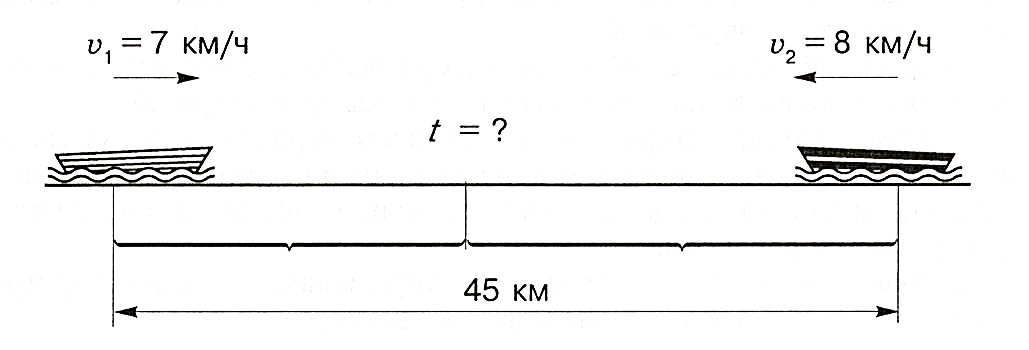
Объяснение

Нам известны скорость первой лодки и скорость второй лодки. Складывая эти скорости, мы можем найти скорость сближения лодок. Эта скорость показывает, на какое расстояние лодки приблизятся друг к другу за 1 час. Зная скорость сближения лодок, мы можем найти, за какое время они преодолеют расстояние в 45 км.

Решение

1) 7 +8 = 15 (км/ч) — скорость сближения лодок.

2) 45: 15 = 3 (ч)

Ответ: лодки встретятся через 3 часа.

б. Из двух населённых пунктов, расстояние между которыми равно 490 км, выехали одновременно навстречу друг другу два мотоциклиста. Скорость первого мотоциклиста — 50 км/ч. Мотоциклисты встретились и продолжили своё движение. Через 6 ч после начала движения расстояние между ними стало равным 50 км. Найдите скорость второго мотоциклиста.

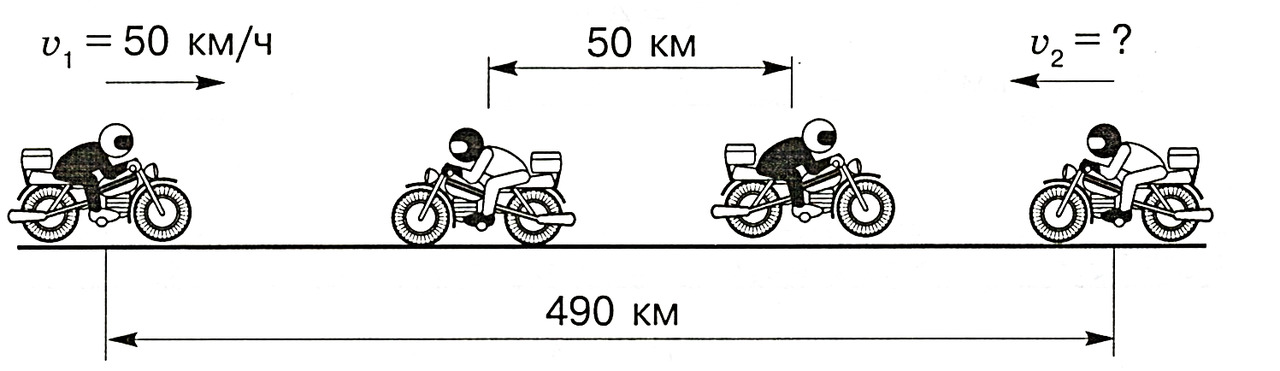
Объяснение

Нам известны скорость первого мотоциклиста и время, которое прошло с начала движения. Мы можем найти расстояние, пройденное первым мотоциклистом. Для этого умножим скорость этого мотоциклиста на время движения. Найдя расстояние, пройденное первым мотоциклистом, можно найти расстояние, пройденное вторым. Для этого из расстояния между двумя населёнными пунктами вычтем расстояние, пройденное первым мотоциклистом, и добавим к нему ещё 50 км. Время дви­жения обоих мотоциклистов одинаковое, 6 ч. Зная расстояние, пройден­ное вторым мотоциклистом, и время движения, мы можем найти его скорость. Для этого разделим расстояние на время.

Решение

1) 50 · 6 = 300 (км) — расстояние, пройденное первым мотоциклис­том за 6 ч.

2) 490 — 300 +50 = 240 (км) — расстояние, пройденное вторым мо­тоциклистом за 6 ч.

3) 240: 6 = 40 (км/ч)

Ответ: скорость второго мотоциклиста — 40 километров в час.

в. Два велосипедиста выехали одновременно на­встречу друг другу из двух населённых пунктов, рассто­яние между которыми составляет 150 км. Скорость пер­вого велосипедиста равна 15 км/ч, скорость второго ― 20 км/ч. Найдите расстояние, которое будет между ве­лосипедистами через 4 ч.

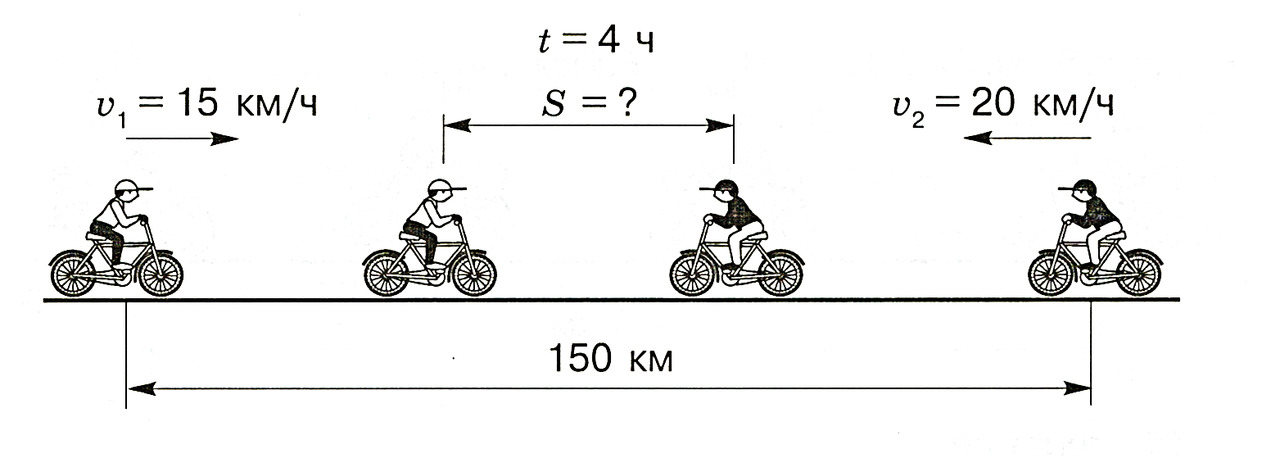
Объяснение

Нам известны скорость первого и скорость второго велосипедистов. Складывая эти скорости, мы можем найти скорость их сближения. Эта скорость показывает, на какое расстояние велосипедисты приблизятся друг к другу за 1 час. Зная скорость сближения велосипедистов, можно найти расстояние, которое они преодолеют за 4 ч. Для того чтобы определить, какое расстояние будет между велосипедистами через 4 ч, вычтем из 150 км общее расстояние, которое пройдено ими.

Решение

1) 15 +20 = 35 (км/ч) — скорость сближения велосипедистов.

2) 35 · 4 = 140 (км) ― общее расстояние, пройденное велосипедистами за 4 ч.

3) 150 — 140 = 10 (км)

Ответ: через 4 часа пути расстояние между велосипедистами будет равно 10 километрам.

г. От двух пристаней вышли одновременно навстречу друг другу две лодки. Скорость первой лодки — 17 км/ч, скорость второй — 12 км/ч. Лодки встретились и продолжили своё движение. Через 5 ч после начала движения расстояние между ними стало равным 40 км. Найдите расстояние между пристанями.

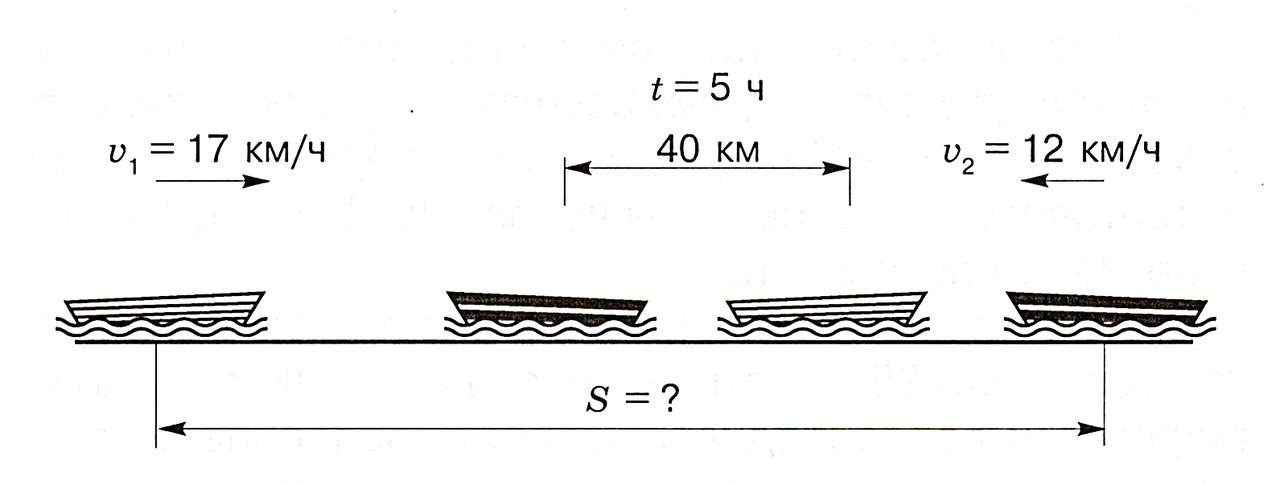
Объяснение

Нам известны скорость первой и скорость второй лодок. Складывая эти скорости, можно найти общую скорость лодок. Через 5 ч лодки встретились и продолжили своё движение, причём расстояние между ними стало равным 40 км. Это означает, что сумма расстояний, пройденных лодками, на 40 км больше расстояния между пристанями. Для того что­бы найти расстояние между пристанями, нужно из суммы расстояний, пройденных лодками, вычесть 40 км.

Решение

1) 17 +12 = 29 (км/ч) — общая скорость лодок.

2) 29 · 5 = 145 (км) — общее расстояние, пройденное обеими лод­ками.

3) 145 — 40 = 105 (км)

Ответ: расстояние между пристанями равно 105 километрам.

Решите задачи:

1. От двух станций, расстояние между которыми рав­но 660 км, вышли одновременно навстречу друг другу два поезда. Скорость первого поезда — 50 км/ч. Найди­те скорость второго поезда, если поезда встретились через 6 ч.

2. Два велосипедиста выехали одновременно на­встречу друг другу из двух посёлков. Скорость первого велосипедиста — 17 км/ч, скорость второго — 14 км/ч. Встретились велосипедисты через 3 ч. Найдите рассто­яние между посёлками.

3. Из двух населённых пунктов, расстояние между ко­торыми равно 95 км, отправились навстречу друг другу пешеход и велосипедист. Скорость велосипедиста — 17 км/ч, скорость пешехода — 5 км/ч. Найдите расстоя­ние, которое будет между ними через 5 ч.

4. От двух лодочных станций, расстояние между ко­торыми равно 83 км, вышли одновременно навстречу друг другу две лодки. Скорость первой лодки — 7 км/ч, скорость второй — 9 км/ч. Лодки встретились и продол­жили своё движение. Найдите время, через которое расстояние между лодками будет составлять 29 км.

5. От двух станций, расстояние между которыми равно 610 км, вышли одновременно навстречу друг два поезда. Скорость первого поезда — 70 км/ч. Поезда встретились и продолжили своё движение. Через 5 ч расстояние между ними стало равным 60 км. Найдите скорость второго поезда.

6. Из двух посёлков вышли одновременно навстречу друг другу два пешехода. Скорость первого пешехода — 4 км/ч, скорость второго — 6 км/ч. Пешеходы встретились и продолжили своё движение. Через 6 ч расстояние между ними стало равным 10 км. Найдите расстояние между посёлками.

7. Два мотоциклиста выехали одновременно навстречу друг другу из двух населённых пунктов, расстояние между которыми составляет 500 км. Скорость первого мотоциклиста — 65 км/ч, скорость второго — 70 км/ч. Найдите расстояние, которое будет между мотоциклистами через 3 ч.

8. От двух станций, расстояние между которыми равно 610 км, вышли одновременно навстречу друг другу два поезда. Скорость первого поезда — 50 км/ч. Через 5 ч им осталось проехать до встречи друг с другом ещё 60 км. Найдите скорость второго поезда.

9. Два велосипедиста выехали одновременно навстречу друг другу из двух посёлков. Скорость первого: велосипедиста — 17 км/ч, скорость второго — 14 км/ч. Через 3 ч им оставалось проехать до встречи друг с другом ещё 16 км. Найдите расстояние между посёлками.

10. Два автомобиля выехали одновременно навстре­чу друг другу из двух городов, расстояние между кото­рыми равно 800 км. Скорость первого автомобиля — 60 км/ч, скорость второго — 70 км/ч. Найдите время, че­рез которое автомобилям до встречи друг с другом ос­танется проехать 20 км.

ЗАДАЧИ НА ДВИЖЕНИЕ В ПРОТИВОПОЛОЖНЫХ НАПРАВЛЕНИЯХ

а. Из одной деревни в противоположных направлени­ях выехали одновременно два автомобиля. Через 5 ч расстояние между ними стало равным 1000 км, из ко­торых 55% проехал второй автомобиль. Найдите ско­рость каждого автомобиля.

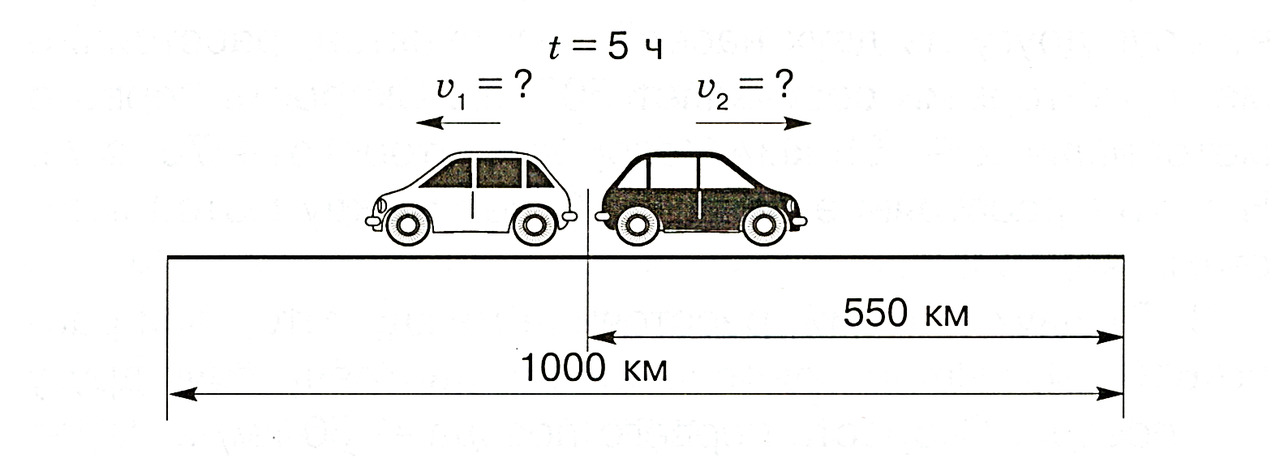
Объяснение

Нам известно расстояние, которое стало между автомобилями через 5 ч; известно, что автомобили выехали одновременно из одной дерев­ни и что 55% расстояния между ними проехал второй автомобиль. Сле­довательно, мы можем найти расстояние, пройденное вторым автомо­билем. Для этого переведём 55% в дробь (55% = 55/100). Разделим расстояние 1000 км на 100 и умножим на 55. Мы нашли расстояние, пройденное вторым автомобилем.

Для того чтобы найти расстояние, пройденное первым автомобилем, вычтем из общего расстояния, пройденного обоими автомобилями, расстояние, пройденное вторым. Теперь мы можем найти скорости каждого автомобиля. Для этого разделим расстояние, пройденное каждым автомобилем, на время, прошедшее с начала их движения.

Решение

1) 1000: 100 · 55 = 550 (км) — расстояние, пройденное вторым автомобилем.

2) 1000 — 550 = 450 (км) — расстояние, пройденное первым автомобилем.

3) 550: 5 = 110 (км/ч) — скорость второго автомобиля.

4) 450: 5 = 90 (км/ч) — скорость первого автомобиля.

Ответ: скорость первого автомобиля — 90 километров в час, скорость второго автомобиля — 110 километров в час.

б. От пристани в противоположных направлениях вышли одновременно два катера. Скорость первого катера — 17 км/ч, скорость второго катера — 12 км/ч. Найдите время, через которое расстояние между ними будет равно 87 км.

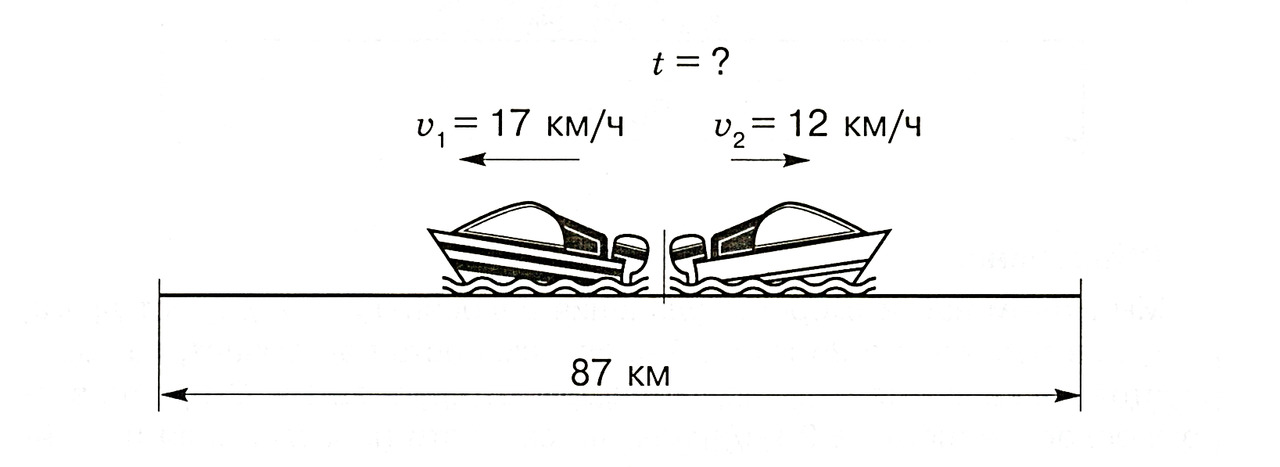
Объяснение

Нам известны скорость первого и скорость второго катеров. Складывая эти скорости, мы можем найти скорость удаления катеров друг от друга. Эта скорость показывает, на какое расстояние катера удалятся друг от друга за 1 ч. Зная эту скорость, можно найти, через какое вре­мя расстояние между катерами будет равно 87 км.

Решение

1) 17 +12 = 29 (км/ч) — скорость удаления катеров друг от друга.

2) 87: 29 = 3 (ч)

Ответ: катера удалятся друг от друга на 87 километров через 3 часа.

в. От турбазы в противоположных направлениях вы­ехали одновременно два велосипедиста. Через 3 ч рас­стояние между ними стало равным 96 км. Скорость пер­вого велосипедиста на 2 км/ч больше скорости второго велосипедиста. Найдите скорость каждого велосипеди­ста.

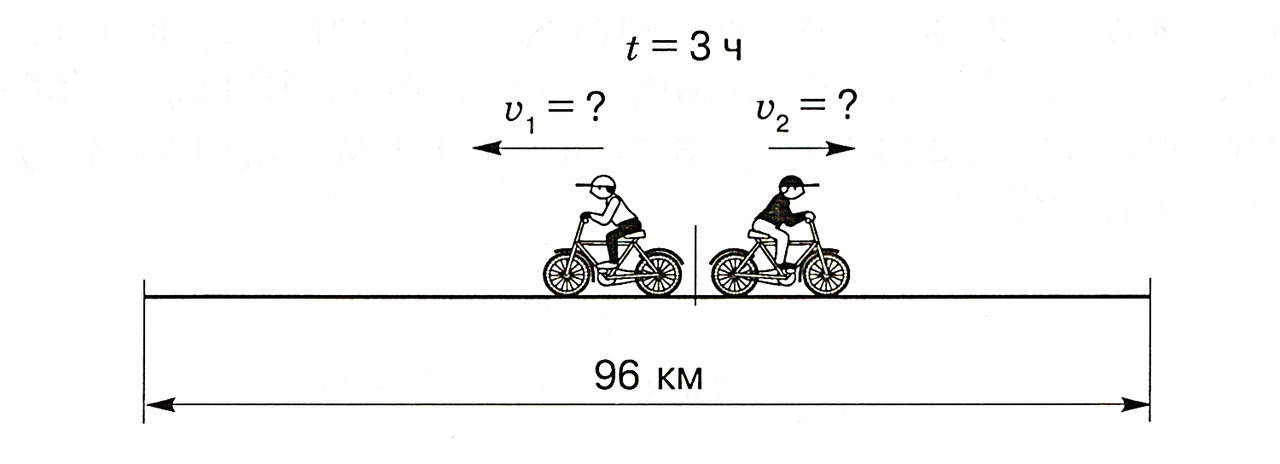
Объяснение

Мы можем найти скорость удаления велосипедистов друг от друга, разделив расстояние 96 км на 3 ч. Эта скорость показывает, на какое расстояние велосипедисты удалятся друг от друга за 1 ч. Скорость вто­рого велосипедиста на 2 км/ч меньше скорости первого. Если из най­денной скорости удаления вычесть 2 км/ч, то мы получим удвоенную ско­рость второго велосипедиста. Для того чтобы найти скорость первого велосипедиста, прибавим 2 км/ч к только что найденной скорости вто­рого велосипедиста.

Решение

1) 96: 3 = 32 (км/ч) — скорость удаления велосипедистов друг от друга.

2) 32 — 2 = 30 (км/ч) — удвоенная скорость второго велосипедиста.

3) 30: 2 = 15 (км/ч) — скорость второго велосипедиста.

4) 15 +2 = 17 (км/ч) — скорость первого велосипедиста.

Ответ: скорость первого велосипедиста — 17 километров в час, скорость второго велосипедиста — 15 километров в час.

г. Из одной деревни в противоположных направлениях вышли одновременно два пешехода. Через 8 ч расстояние между ними стало равным 96 км. Расстояние, которое прошёл первый пешеход, на 16 км больше расстояния, которое прошёл второй пешеход. Найдите скорость каждого пешехода.

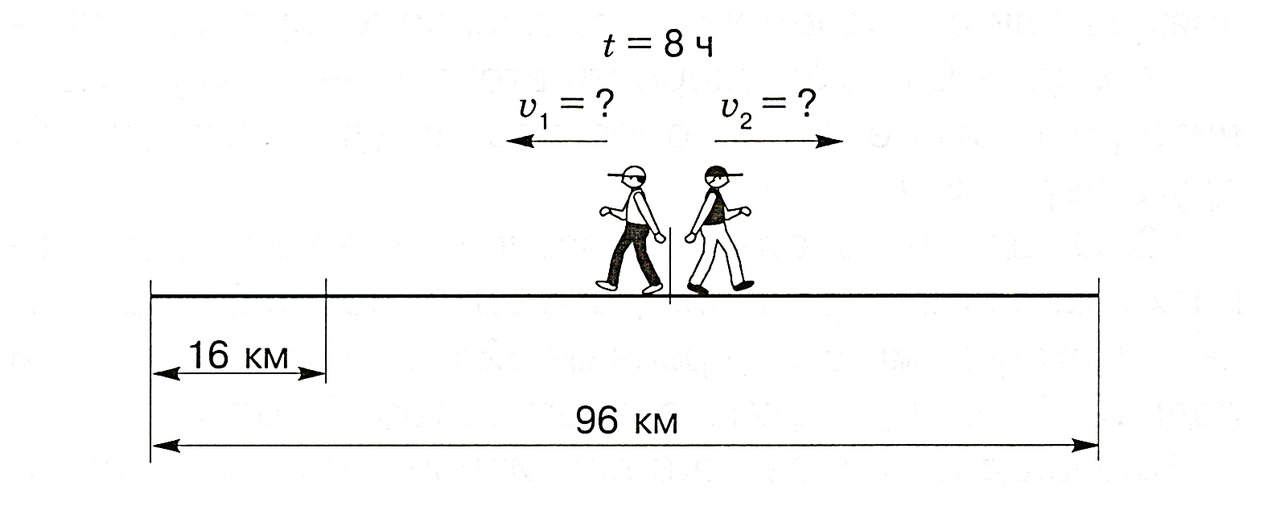
Объяснение

Мы можем найти скорость удаления пешеходов друг от друга, разделив расстояние 96 км на 8 ч. Эта скорость показывает, на какое расстояние пешеходы удалятся друг от друга за 1 ч. За 8 ч после начала движения первый пешеход прошёл на 16 км больше второго, следовательно, мы можем узнать, на сколько первый пешеход проходил за 1 ч больше, чем второй. Для этого разделим 16 км на 8 ч. Если из найденной скорости удаления отнять разность скоростей обоих пешеходов, то мы найдём удвоенную скорость второго пешехода. Для того чтобы найти скорость первого пешехода, прибавим разность скоростей к только что найденной скорости второго пешехода.

Решение

1) 96: 8 = 12 (км/ч) — скорость удаления пешеходов.

2) 16: 8 = 2 (км/ч) — разность скоростей пешеходов.

3) 12 — 2 = 10 (км/ч) — удвоенная скорость второго пешехода.

4) 10: 2 = 5 (км/ч) — скорость второго пешехода.

5) 5 +2 = 7 (км/ч) — скорость первого пешехода.

Ответ: скорость первого пешехода — 7 километров в час, скорость второго пешехода — 5 километров в час.

Решите задачи:

11. От одной станции в противоположных направле­ниях вышли одновременно два поезда. Скорость перво­го поезда — 60 км/ч, скорость второго — 70 км/ч. Най­дите расстояние, на которое поезда удалятся друг от друга через 3 ч.

12. От одной пристани в противоположных направле­ниях вышли одновременно две лодки. Через 2 ч рассто­яние между ними стало равным 32 км. Скорость первой лодки — 7 км/ч. Найдите скорость второй лодки.

13. Из одного посёлка в противоположных направле­ниях выехали одновременно грузовой автомобиль и ве­лосипедист. Скорость автомобиля — 40 км/ч, скорость велосипедиста составляет 1/2 скорости автомобиля. Найдите время, через которое расстояние между ними будет равно 120 км.

14. Из одного населённого пункта в противоположных направлениях выехали одновременно две машины. Скорость первой машины — 100 км/ч, скорость второй машины составляет 70% скорости первой. Найдите расстояние, которое будет между машинами через 3 ч.

15. От одной пристани в противоположных направлениях вышли одновременно два теплохода. Скорость первого теплохода — 25 км/ч. Скорость второго теплохода на 1/5 часть больше скорости первого. Найдите расстояние, которое будет между теплоходами через 4 ч.

16. От турбазы в противоположных направлениях вышли одновременно два туриста. Через 5 ч расстояние между ними стало равным 45 км. Скорость первого туриста на 1 км/ч больше скорости второго туриста. Найдите скорость каждого туриста.