Бесплатный фрагмент - Определение положения в космосе на основе сопоставления изображения с 3D-цифровой моделью поверхности

Определение положения в космосе на основе сопоставления изображения с 3D цифровой моделью поверхности

Шахулов Никита Ренарьевич — специалист по геоинформационным системам и геомаркетингу, Инновационный-образовательный Центр космических услуг ОАО «НПК „РЕКОД“», г. Волгоград

Член — Русского Космического Общества, Американского геофизического союза

Аннотация:

Разработка точной оценки положения бортовой камеры является одной из основных задач спутниковых систем, и попытки улучшить точность положения камеры дистанционного зондирования никогда не прекращаются. Положение камеры может быть восстановлено путем выравнивания захваченного 2D-изображения и 3D-цифровой модели поверхности соответствующей сцены. В этой статье предлагается новый метод оценки положения камеры по захваченным изображениям с использованием более известных 3D-продуктов real scene для повышения точности определения положения камеры дистанционного зондирования. Целью этой оценки является определение положения камеры исключительно по изображению, основанному на известной 3D-модели, где 3D-продукты с очень высоким пространственным разрешением проецируются на пространство изображения системой виртуальной камеры с содержащимися в ошибках начальными параметрами внешней ориентации, и можно ли определить положение камеры. точно зависит от результата 2D–3D регистрации. Процесс состоит из двух этапов: извлечение признаков и измерение, и регистрация сходства. Кроме того, предлагаемый способ пересматривает матрицу вращения и вектор перемещения, используя формулировку, основанную на кватернионном представлении вращения, соответственно. Я оцениваю метод на сложных данных моделирования, и результаты показывают, что может быть достигнута приемлемая точность положения камеры.

Ключевые слова: спутник, физика, математика, астрофизика, 3D-модели, спутниковые снимки, кватернион, фотограмметрия, компьютерное зрение, AR, VR.

Вступление

1.1 Фон

Во многих областях, таких как автономная навигация, 3D-реконструкция и непрерывное моделирование города, можно извлечь выгоду из точной информации о местоположении и ориентации камер или датчиков. В частности, разработка точного положения бортовой камеры является одной из основных задач спутниковой системы, и поэтому некоторые исследователи посвятили себя этой области. Однако оценка положения камеры по-прежнему остается проблемой в области дистанционного зондирования. В качестве потенциального метода решения этой проблемы была разработана оптическая полезная нагрузка для определения ориентации спутника, которая может отвечать критическим требованиям к небольшим низкоорбитальным спутникам, таким как качество освещения, малый объем и низкое энергопотребление. Кроме того, вычислительная производительность бортового компьютера может быть значительно улучшена с помощью графического процессора (GPU). Взятые вместе, бортовой компьютер может обрабатывать изображение, полученное с помощью пульта дистанционного управления, зондирующая камера на орбите и определяет отклонение позы. В этом контексте была проведена структура регистрации изображения в модель с использованием контекстно-зависимого геометрического хэша [5, 6]. В [5] объекты с обрезными углами и контекстные объекты использовались для решения проблемы неоднозначности сопоставления при регистрации отдельных изображений с известными моделями 3D-зданий без текстуры. Это указывает на то, что фундаментальным шагом для облегчения позирования в космосе является согласованная регистрация данных дистанционного зондирования, полученных в разные эпохи, с существующими 3D-моделями. Авторы в [6] стремились оценить положение спутника путем сопоставления изображений наблюдения и известных изображений базовой карты.

В последнее время генерация крупномасштабных 3D-моделей получила значительный прорыв благодаря значительному развитию фотограмметрии и компьютерного зрения. Кроме того, постоянно развивающийся интернет высококачественных 3D-продуктов привел к разрушительным результатам [7]. В результате существует множество поставщиков высокоточных и высококачественных продуктов для создания 3D-моделей, таких как Google Earth, Maxar, Airbus и Microsoft Maps. На сегодняшний день самая точная 3D-модель, созданная на основе спутниковых снимков, может достигать точности 3 м@SE

(ошибка 3 м с SE90, что является аббревиатурой 90-го процентиля сферической ошибки) с ведущими компаниями, которые обеспечивают разрешение 0,5 м и абсолютную точность 3 м 3D-модель поверхности с текстурами со всех сторон. Высокое качество этих доступных продуктов обеспечивает прочную основу для этой работы. Это делает оценку положения камеры с помощью более известной 3D-модели поверхности реальной сцены многообещающим подходом в области дистанционного зондирования. Кроме того, новые технологии дополненной реальности (AR), виртуальной реальности (VR) и цифровых двойников позволяют использовать 3D-архитектурные модели в качестве интерактивных инструментов на компьютерах или мобильных устройствах.

1.2 Сопутствующая работа

Определенное внимание было уделено исследовательской работе, связанной с поиском способов сопоставления изображения с моделью для оценки положения камеры как в академических кругах, так и в промышленности. В этом разделе дается краткий обзор соответствующей структуры, которая в основном фокусируется на соответствующих методах оценки позы. Современные подходы к мультимодальной 2D-3D регистрации можно в целом разделить на два типа: (1) типичные методы, основанные на геометрии, и (2) методы регрессии позы, основанные на машинном обучении, которые подробно рассматриваются ниже.

Типичные методы, основанные на геометрии: Типичные методы, основанные на геометрии, реализуются путем установления соответствующей взаимосвязи между захваченным изображением и 3D-моделью. Как правило, процесс регистрации изображения в модель включает в себя три этапа: (1) извлечение признаков, (2) измерение сходства и сопоставление и (3) оценка положения камеры. Характерные особенности — это наиболее распространенные точки, которые обнаруживаются как на захваченном изображении, так и в 3D-модели, такие как края, контурные линии, точки пересечения и углы, а также используются в процессе сопоставления изображений [5, 8—12]. Необходимо проявлять особую осторожность, чтобы убедиться, что эти особенности различимы, хорошо распределены и могут быть надежно обнаружены в наборах данных изображений и 3D-моделей. В отличие от методов внешних датчиков, таких как инерциальные измерительные устройства (IMU), Cai и Ye [13] использовали предварительную информацию об ориентации изображения дистанционного зондирования в качестве ссылки, а положения захваченных изображений корректировались на основе отклонения ориентации между камерой запроса и эталонной камерой. На основе информации об ориентации спутника, которая была извлечена из спутникового изображения дистанционного зондирования, ориентация спутника была рассчитана на основе смещения между спутниковым изображением в реальном времени и эталонным изображением. Этот метод позволяет не только точно измерить ошибки ориентации осей крена и тангажа, но и измерить ось рыскания. Янг и Чен [14] предложили метод сопоставления изображений беспилотных летательных аппаратов (БПЛА) с данными лидара, в котором контур зданий сравнивался с величиной тензорного градиента на изображении для оценки параметров внешней ориентации (EOPs) изображения. Смещение между изображением в реальном времени и эталонным изображением было получено на основе таких методов, как обработка изображений. Этот метод обеспечивает точное измерение положения камеры на основе начальной внешней ориентации изображения. Была рассмотрена новая схема гибридного консенсуса случайной выборки (RANSAC) для улучшения оценки положения камеры как для 2D-3D, так и для 2D-2D совпадений [15], в которой подходящий решатель может быть автоматически выбирается из гибридных различных минимальных решателей на каждой итерации.

Крупномасштабное визуальное географическое местоположение было опубликовано в [16]. В этой работе подробно обсуждалась двунаправленная взаимосвязь между изображением и местоположением, были всесторонне рассмотрены новейшие технологии в области крупномасштабной визуальной географической локации, а также обсуждалась новая тенденция в этой области. В частности, регистрация 2D–3D является ключевым шагом для создания эталонной цифровой 3D-модели земли [17—19]. Использование прямых методов 2D–3D регистрации показало лучшую производительность с точки зрения улучшения производительности регистрации [20]. В [20], применяя квантование визуального словаря и приоритетный поиск соответствия, была изучена проблема быстрой локализации на основе изображений на основе эффективного прямого сопоставления 2D-3D. Стремясь решить такие проблемы, как масштабируемость и неоднозначность из–за прямого метода сопоставления 2D–3D, в [21] был исследован принципиальный подход глобального сопоставления 2D-3D, в котором для достижения локализации камеры использовалась глобальная контекстуальная информация из обоих наборов данных. Чжао и др. [22] представили надежный метод измерения сходства для сканирования 2D-изображения в 3D-диапазоне, собранного в городских сценариях с использованием недорогих и высококачественных датчиков путем вычисления измерений сходства между набором пар атрибутов 2D–3D. Автоматический и точный метод сопоставления изображения с моделью был предложен в [23], где для выполнения регистрации использовался алгоритм оптимизации роя частиц (PSO). PSO объединил разреженные и плотные объекты, чтобы значительно увеличить их сильные стороны, независимо от модальностей как изображения, так и 3D-модели. Однако качество регистрации, на которое влияют параметры PSO, нуждается в более детальном анализе. PSO также может быть использован для уточнения перевода между двумя различными представлениями [24]. Ли и др. [24] предложили автоматический и не требующий маркеров метод регистрации для точной регистрации, основанный на семантических признаках, извлеченных из панорамных изображений и облаков точек. Глобальная система позиционирования (GPS) и IMU использовались для предоставления некоторых вспомогательных средств для структуры из движения (SfM) для оценки точной матрицы вращения между панорамной камерой и лазерным сканером.

Для метода PSO параметры могут оказывать некоторое негативное влияние на оценку внешней ориентации камеры. Чтобы справиться с этим недостатком, был использован метод поиска глобальной оптимизации, основанный на ветвлении и привязке (BnB). Этот метод находит новые верхние и нижние границы целевой функции путем преобразования задачи сопоставления 2D-3D в задачу оптимизации. При решении задачи оценки позы такого типа могут быть сформированы две стратегии сопоставления набора точек, а именно: фиксация набора точек 3D и фиксация набора точек 2D и системы координат проекции. Первый находит оптимальную ориентацию и положение камеры в соответствии с полученными изображениями cam-era и набором 2D-точек. Последний приводит набор точек 2D-проекции, который был извлечен из проекции 3D-точки, в соответствие с набором точек 2D путем нахождения соответствующих внешних параметров камеры. Эти две стратегии сопоставления гарантируют глобальный оптимум без предварительной информации о позе [25, 26]. Однако у этого метода есть и свой недостаток: большое пространство поиска увеличивает временные затраты и вычислительную сложность.

Методы регрессии позы на основе машинного обучения изучают соответствующую взаимосвязь между изображениями и 3D-объектами сцены из обучающих выборок с различными ориентациями и положениями. Правила принятия решений и регрессионные функции обучения также применяются к выборкам, и полученные результаты используются в качестве оценки отношения тестовых выборок. Метод, основанный на обучении, может улучшить производительность позирования камеры при позиционировании монокулярных изображений с шестью степенями свободы (6DOF) и демонстрирует большие перспективы в области 3D-модели положения камеры. Было предложено несколько решений для работы с сквозной сетью. Кендалл и др. [27] представили сверточную нейронную сеть (CNN), основанную на монокулярной системе повторной локализации 6DOF в реальном времени, чтобы возвращать позу камеры из одного изображения RGB сквозным способом без каких-либо дополнительных вспомогательных условий. Обучающая метка CNN была сгенерирована автоматически из видеозаписи сцены с помощью SfM и многовидового стерео (MVS). Затем обучение передаче было использовано для определения перемещения в крупномасштабных наборах данных классификации, что стало первым применением CNN в сквозном позиционировании положения камеры 6DOF. Ву и др. [28] представили три технологии перемещения камеры на основе CNN и провели углубленное исследование и анализ CNN для перемещения камеры. Все методы, упомянутые выше, могут работать только тогда, когда информация о глубине недоступна, что является наиболее очевидным ограничением CNN в физической области.

Единая сквозная сеть также использовалась для решения задачи оценки позы 6DoF по одиночным монокулярным изображениям RGB [29, 30]. Байесовский PoseNet был представлен для достижения сквозной последовательности, а неопределенность изменения положения была получена с помощью апостериорного распределения из байесовских весов CNN. Как PoseNet [27], так и байесовские модели PoseNet [30] показали отличную производительность в условиях перемещения внутри и снаружи помещений. Работа в [27] была расширена, чтобы решить проблему с настройкой суперпараметров функции потерь в PoseNet, представив более базовую теоретическую обработку и исследовав множество новых функций потерь для изучения положения камеры на основе ошибок геометрии и перепроекции сцены. Кендалл и Чиполла [31] использовали функцию геометрических потерь для повышения надежности регрессии положения камеры. Виджаянарасимхан и др. [32] предложили подход SFM-NET, который представлял собой геометрическую чувствительную нейронную сеть для оценки движения видео. Он может декомпозировать движение пикселя от кадра к кадру в соответствии с глубиной сцены и объекта, движением камеры и вращением, и перемещением 3D-объекта. Модель обучения с подкреплением также может быть использована для решения задачи регистрации 2D–3D, такой как модель выбора характерного вида (CVSM), которая может эффективно повысить вычислительную эффективность и снизить частоту отклонений. Однако все чаще возникает озабоченность по поводу того, что существующие методы не могут учитывать непрерывность изображений. Некоторые из этих методов либо слишком сложны, либо слишком велики для вычисления, и ограничены физической областью и объемом известных данных, что неудобно для крупномасштабного определения положения камеры.

Хотя многие исследователи пытаются решить проблему, связанную с оценкой позы с помощью встроенной камеры, новое решение все еще может быть обеспечено мелкозернистыми 3D-моделями с текстурой. Высокоточная 3D-модель продукта earth является одной из основных целей в этой работе я покажу, как он может эффективно вписаться в алгоритм на основе кватернионов [33] с процедурой оценки положения камеры. Кроме того, направление силы тяжести рассматривалось как потенциальный метод решения проблемы относительной ориентации [34, 35]. Это позволяет нам решить основанную на кватернионах относительную позу с известным направлением силы тяжести. Однако существует проблема регистрации 2D-изображения с помощью 3D-модели с информацией о текстуре, поэтому необходимо использовать конкретные предварительные параметры проекции, а также метод для определения параметров камеры. Оценка положения камеры играет ключевую роль в области дистанционного зондирования. Мотивированный вышеупомянутыми наблюдениями, этот документ намеревается предложить новый метод на основе изображения и реальной 3D-модели сцены для эффективного решения проблемы.

Основным вкладом этой статьи является новая схема оценки положения камеры для космических полетов. Мой ключевой вклад можно резюмировать следующим образом: Я предлагаю новую систему оценки положения камеры на основе захваченных изображений с использованием более известных высокоточных 3D-продуктов, созданных с помощью изображений с несколькими видами, в качестве эталона для повышения точности определения положения камеры дистанционного зондирования. Насколько мне известно, это первая работа, которая успешно восстанавливает позу камеры на основе 3D-модели с реальными текстурами в области дистанционного зондирования.

∙ Я преобразую регистрацию 2D-3D в регистрацию 2D–2D. Затем предлагается основанный на кватернионах метод оценки относительной позы с известным направлением силы тяжести.

∙ Что касается проблемы получения информации о положении и ориентации камеры, используется новая формулировка, основанная на кватернионном представлении вращения. Используя эту формулу, я могу восстановить изменения поворота и перемещения, соответственно, без использования матрицы гомографии.

Остальная часть этого документа организована следующим образом. Предложенный метод на основе 3D-модели описан в разделе 2. Затем экспериментальный анализ и обсуждение результатов представлены в разделе 3. Наконец, в конце делаются выводы.

2 Методология

Целью данного исследования является точное получение параметров поворота и перемещения фактического изображения, полученного в реальной среде, по отношению к 3D-модели. Там в переводе между двумя изображениями можно восстановить только до масштаба. Я преобразую задачи позирования в полиномиальные задачи в терминах вектора кватернионов, где оценка относительной ориентации между двумя изображениями решается для формирования более простого уравнения с использованием направления силы тяжести. Когда матрица вращения получена, вектор перемещения можно восстановить, поместив матрицу вращения в ограничение формулы. Представленный подход состоит из трех основных этапов: (1) перспективная проекция и регистрация, (2) точное кватернионное представление оценки матрицы вращения с помощью геометрических ограничений и (3) точная оценка вектора перевода. В частности, на протяжении всей этой статьи я предполагаю, что камера откалибрована, что

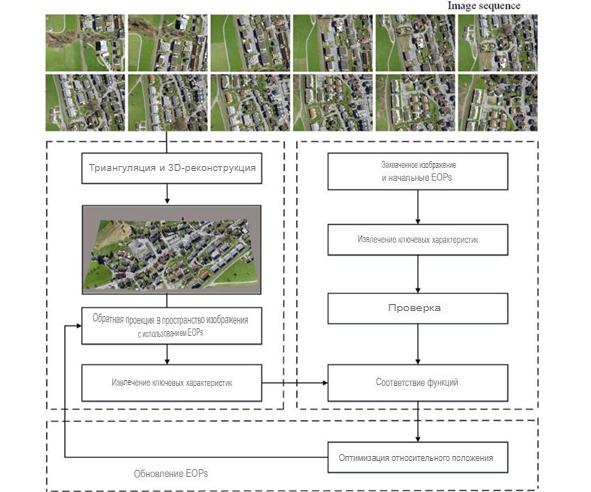
РИСУНОК 1 Блок-схема предлагаемого метода оценки положения камеры

означает, что внутренние параметры известны. Обратите внимание, что эта внутренняя матрица может быть легко решена в контролируемой среде с помощью существующего подхода к калибровке камеры (например, калибровка Чжана). Как правило, в соответствиях существуют выбросы, подход RANSAC используется для уменьшения влияния выбросов в такого рода работах, чтобы гарантировать правильное сопоставление характерных точек. Ключевые этапы предлагаемой структуры проиллюстрированы на рисунке 1 и дополнительно проработаны следующим образом

2.1 Формулировка проблемы

Система координат модели регистрации 2D–3D показана на рисунке 2. W обозначает систему отсчета 3D-модели, таким образом, задается положение 3D-точек и камер относительно этой 3D-системы отсчета. C обозначает опорный кадр захваченного изображения IC, а P обозначает опорный кадр проекционного изображения Ip с исходным EOPs. XC обозначает проективное преобразование между W и IC. T обозначает преобразование между C и P. Процесс ввода состоит из одного реального захваченного изображения и высокоточной 3D-модели сцены, которая состоит из точек, координаты которых заданы в системе отсчета W. Регистрация начинается с обратного проецирования существующей 3D-модели здания в пространство изображений с использованием начального (или обновленного на более поздних этапах) EOPs, где пространство изображения представляет собой координату проекции 3D-модели P. Отсчетный кадр C положения камеры захваченного изображения состоит из положения и ориентации относительно 3D-отсчета W. Здесь в данной работе рассматриваются традиционные перспективные камеры.

Пусть поворот и перемещение кадра камеры между двумя видами представлены матрицей поворота R и вектором перемещения t соответственно. Классическое решение проблемы позы

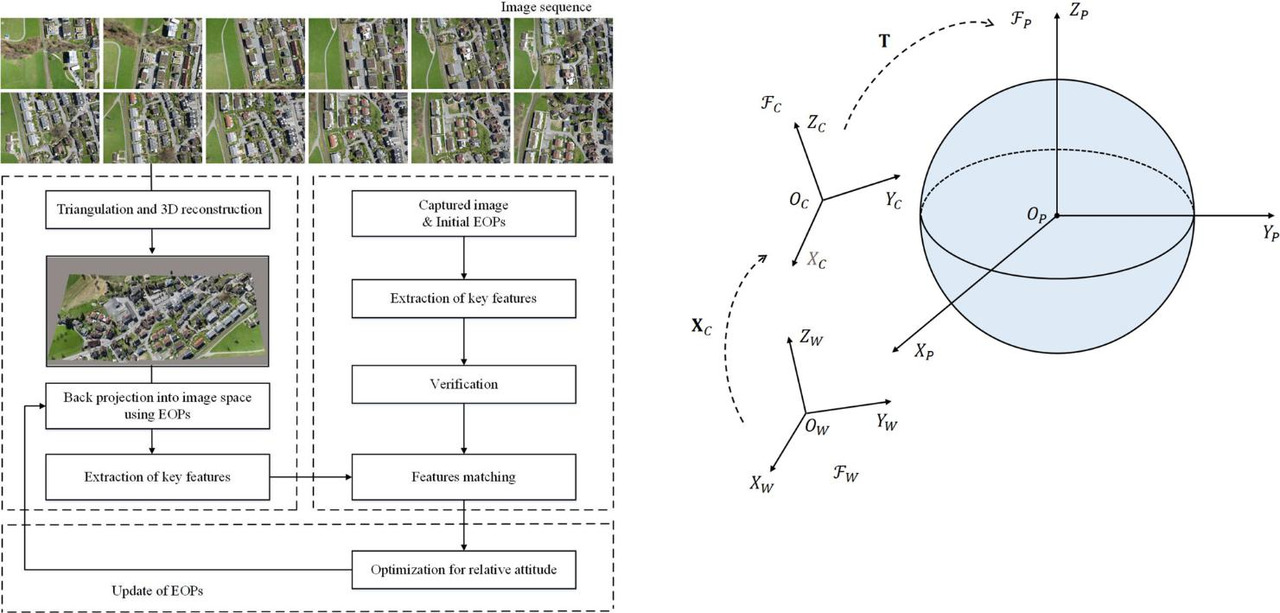
РИСУНОК 2 Иллюстрация модели преобразования системы координат.

W обозначает систему отсчета 3D-модели. C обозначает опорный кадр захваченного изображения, P обозначает опорный кадр проекционного изображения с исходным EOPs

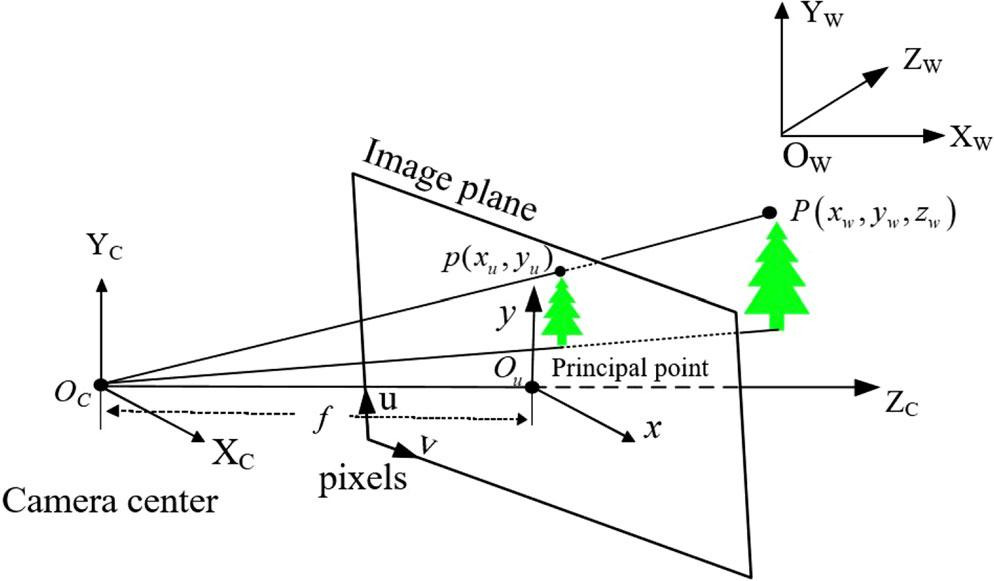
РИСУНОК 3 Модель камеры-обскуры

состоит в том, чтобы установить набор соответствий на основе признаков, а затем решить для (R, t) путем максимизации сходства или минимизации разницы между захваченным изображением IC и эталонным изображением IP, которое берется путем проецирования 3D-модели с неточными EOPs. Здесь оценка позы приводит к проблеме регистрации 2D–2D в случае перспективной камеры [36]. Это может быть выражено как:

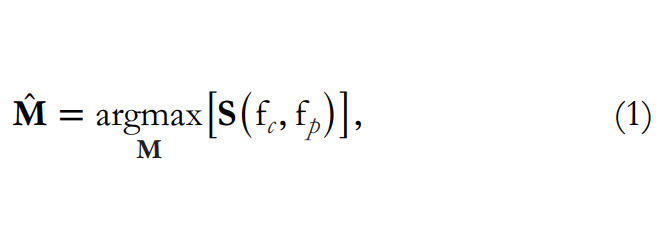
где fc и fp описывают признаки, извлеченные из IC и IP соответственно, а S (⋅) — метрика сходства.