
Бесплатный фрагмент - Об определителях и решении систем линейных уравнений
1.Системы линейных уравнений
1.1.Основные определения
Решением некоторого множества (системы) уравнений f1 (x1,x2,…,xn) = 0,…,fm (x1,x2,…,xn) с неизвестными x1,x2,…,xn
называется множество значений неизвестных, обращающих одновременно все уравнения в тождество [1].
Системой линейных алгебраических уравнений, содержащих m уравнений и n неизвестных, называется система вида:
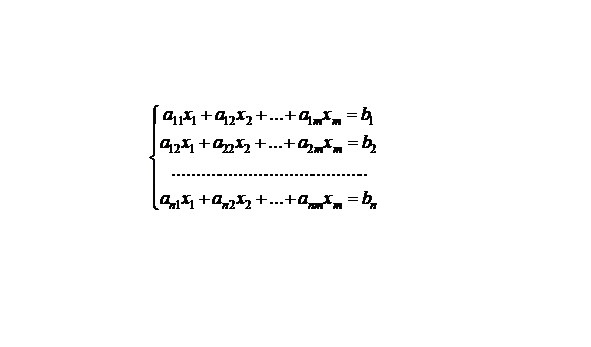
Здесь аij — называется коэффициентом системы, а bij — свободным членом.
Первый индекс коэффициента системы (i) указывает номер уравнения системы в записи на рисунке 1, второй (J) — номер неизвестного, при котором стоит данный коэффициент.
Система линейных алгебраических уравнений называется однородной, если все свободные члены ее уравнений равны нулю.
Система линейных алгебраических уравнений называется неоднородной, если хотя бы один свободный член bij не равен нулю [1].
Решением системы называется n значений неизвестных (х1 = l1, x2 =l2…xn=ln), при подстановке которых в уравнения все уравнения системы обращаются в тождества. Всякое решение системы можно записать в виде матрицы.
Система уравнений называется совместной, если она имеет хотя бы одно решение и несовместной, если она не имеет ни одного решения.
Совместная система называется определенной, если она имеет единственное решение и неопределенной, если имеет более одного решения.
В последнем случае каждое её решение называется частным решением системы. Совокупность всех частных решений называется общим решением. Решить систему, значит выяснить, совместна она или нет, если совместна, то найти её решения.
Две системы называются эквивалентными тогда и только тогда, когда любое решение первой системы является решением второй и любое решение второй системы является решением первой.
Если в системе линейных алгебраических уравнений к одному уравнению прибавить другое, умноженное на любое число (кроме нуля), то полученная таким образом новая система будет эквивалентна исходной.
Если поменять местами уравнения системы, а так же, если перенумеровать неизвестные, то система будет эквивалентна исходной. Можно вычеркнуть уравнение системы, в котором все коэффициенты при неизвестных и свободный член являются нулями.
При решении систем линейных уравнений используется несколько методов:
1.Гаусса
2.Крамера
3.Обратной матрицы.
Для любой системы линейных уравнений существует три ситуации ее решений:
1) одно решение;
2) бесконечное множество;
3) нет решений.
В дальнейшем, при решении системы линейных уравнений различными методами будем предполагать, что теоретическая и практическая части линейной алгебры, посвященные определителям и матрицам, вам знакомы. Если трудности все-таки появятся. то рекомендую обратиться к моей книге и (или) к другой литературе, помещенной в конце этой книги.
2.Решение систем линейных уравнений методом Крамера
Пусть дана система из трех линейных уравнений с тремя неизвестными (см. рис.2б).
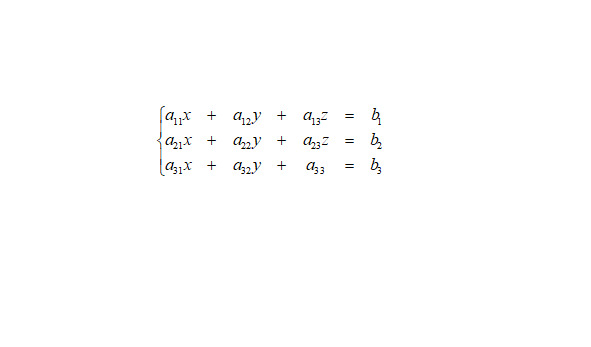
Здесь x, y и z — неизвестные, aij — коэффициенты при неизвестных,
b1 — свободные члены (i = 1,2 и 3; j = 1,2 и 3).
Рассмотрим решение этой системы (рис.2) методом Крамера.
Если определитель этой системы (∆=detA), составленный из ее коэффициентов при неизвестных (см. рис.3) не равен нулю, то система имеет единственное решение (см. рис.4).
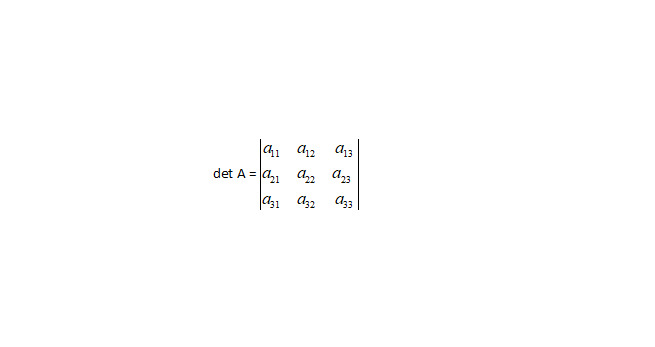
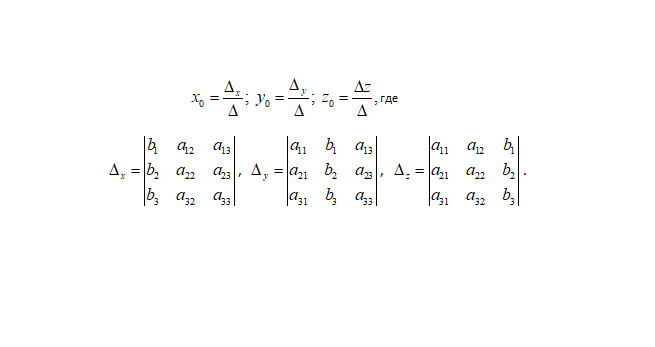
Метод Крамера справедлив и для случая системы из n уравнений и n переменных. однако, при большом n, его использование становится неудобным.
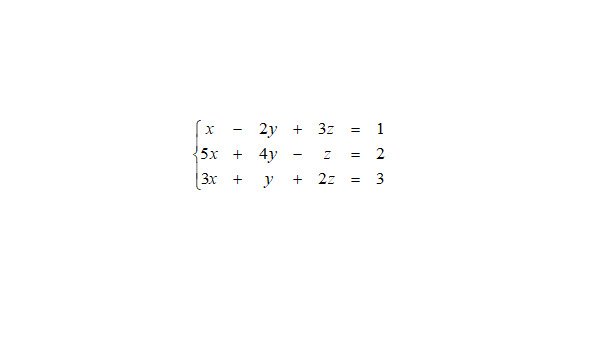
Пример
Решить систему линейных уравнений матричным методом (см. рис.5):
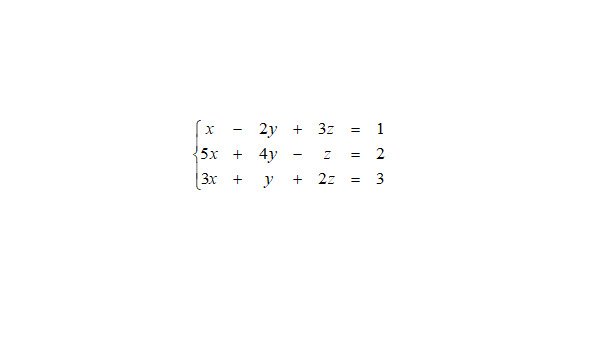
Решение
Данная система, приведенная к матричному виду. выглядит следующим образом (см. рис.10):
Бесплатный фрагмент закончился.
Купите книгу, чтобы продолжить чтение.
