Бесплатный фрагмент - О дифференциальных уравнениях второго порядка и ИИ

Введение

Несколько лет в учебном процессе по математическим дисциплинам в СПбГИК я использовал Электронный Практикум по решению дифференциальных уравнений (ДУ). В Приложении к данной книге имеется глава, в которой приводится инструкция по работе с этим практикумом. В случае приобретения вами любой из моих книг по решению дифференциальных уравнений (смотите спиcок литературы), я готов вам выслать этот практикум бесплатно.

Задания на проведение данной работы можно разделить на две группы:

I. Основные понятия и определения

К этой группе относятся задания 1, 2, 3, и 4.

Их целью является проверка знаний основ решения дифференциальных уравнений.

К формулировке и пояснению некоторых вопросов и ответов на них по данной тематике привлекались нейросети.

II. Решение обыкновенных дифференциальных уравнений второго порядка

К этой группе относится задание 5.

При выполнении данного задания использовались параллельно 3 нейросети.

III. Выполнение заданий

Задание 1

Выберите несколько вариантов ответа. Среди перечисленных дифференциальных уравнений уравнениями второго порядка являются:

РЕШЕНИЕ

Самое простое задание из всех. Здесь понятие степени уравнения в алгебре заменяется на понятие порядка. Нужно только помнить, что речь может идти о порядке производной или порядке дифференциала. В данном случае, дифференциальными уравнениями второго порядка являются 1 и 4 уравнения.

В данном случае, дифференциальными уравнениями второго порядка являются 1 и 4 уравнения.

Задание 2

Отметьте линейные уравнения.

Какие из приведенных дифференциальных уравнений являются линейными?

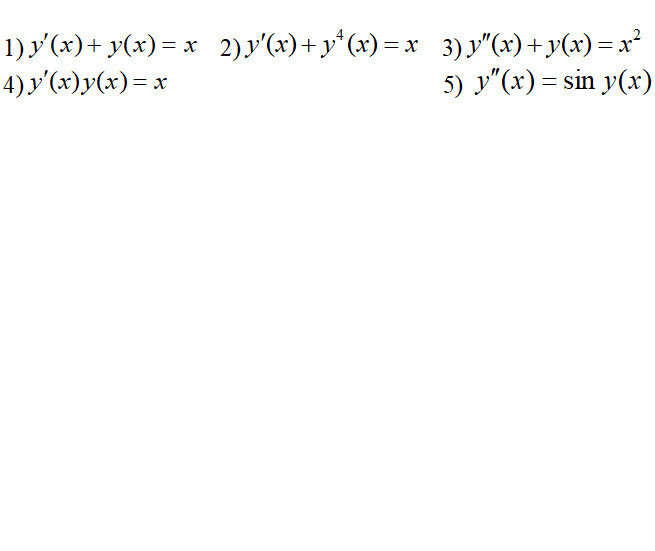
РЕШЕНИЕ

Обратимся к нейросетям.

Давайте рассмотрим каждое из предложенных уравнений и определим, являются ли они линейными.

— Уравнение: y′ (x) +y4 (x) =x

— Это уравнение нелинейное, так как содержит член y4 (x), который является нелинейным по отношению к y.

— Уравнение: y′ (x) ⋅y (x) =x

— Это уравнение нелинейное, так как содержит произведение y′ (x) ⋅y (x), что делает его нелинейным.

— Уравнение: y′′ (x) =sin (x)

— Это уравнение линейное, так как оно является линейным по отношению к y и его производным. Здесь нет нелинейных членов.

— Уравнение: y′′ (x) +y (x) =x2

— Это уравнение линейное, так как оно также является линейным по отношению к y и его производным. Все члены уравнения линейны.

— Уравнение: y′ (x) +y (x) =x

— Это уравнение линейное, так как оно имеет линейные члены по отношению к y и его производной.

Резюме:

— Линейные уравнения: y′′ (x) =sin (x),y′′ (x) +y (x) =x2,y′ (x) +y (x) =x

— Нелинейные уравнения: y′ (x) +y4 (x) =x,y′ (x) ⋅y (x) =x

Просто великолепное решение с самыми подробными пояснениями.

Отметим, что в данном случае к ЛИНЕЙНЫМ уравнениям можно отнести и два дифференциальныx уравнения второго порядка:

y′′ (x) = sin (x) и y′′ (x) +y (x) =x^2

Задание 3

Расставьте приведенные дифференциальные уравнения по возрастанию порядка

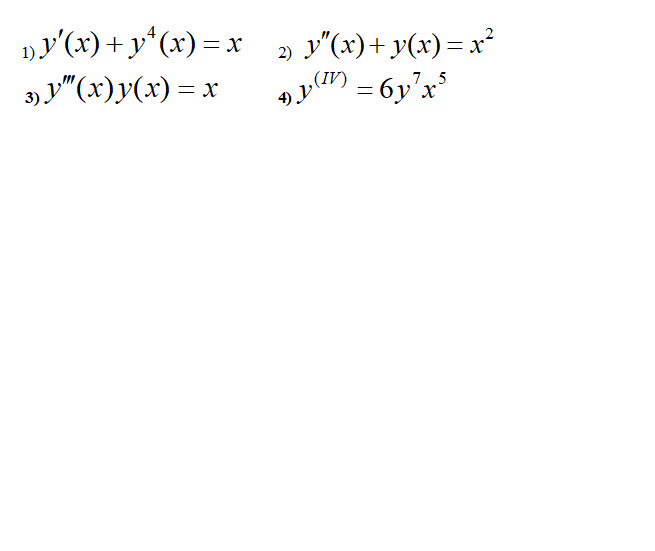
РЕШЕНИЕ

В данном случае ничего изменять ненужно: порядковые номера уравнений находятся в полном соответствии с порядком дифференциального уравнения.

Задание 4

Поставьте в правильное соответствие тип решения дифференциального уравнения с видом функции:

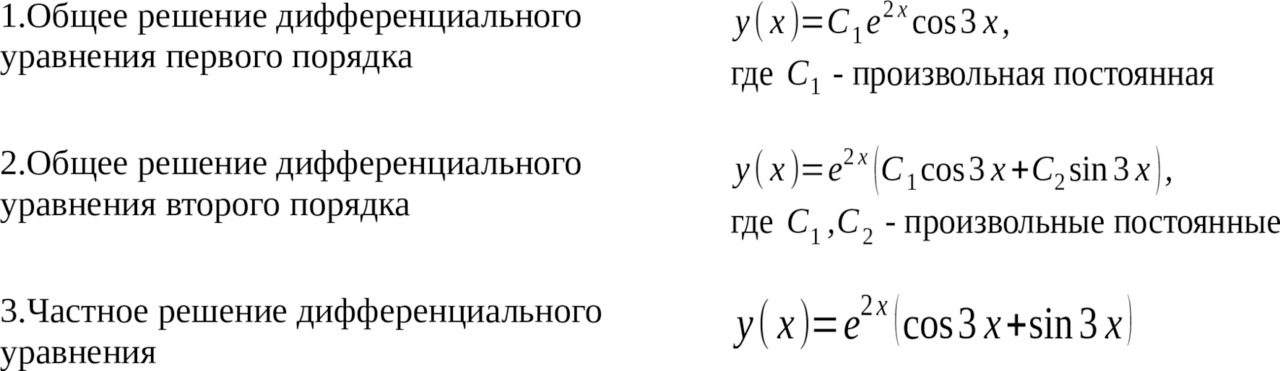
РЕШЕНИЕ

В данном задании все три решения находятся в полном соответствии с типами уравнений.

Задание 5

Найти общее решение дифференциального уравнения второго порядка с постоянными коэффициентами:

О типах и особенностях решения таких дифференциальных уравнений читайте в Приложении I. Информация к размышлению.

РЕШЕНИЕ

Обратимся к нейросетям.

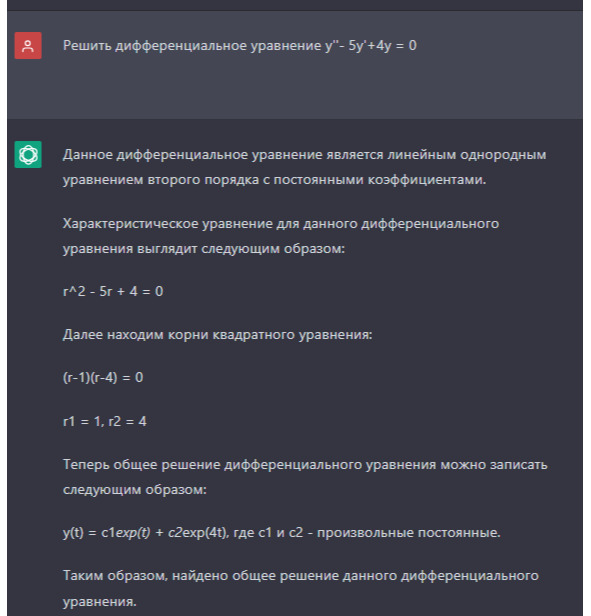
Для решения однородного линейного дифференциального уравнения второго порядка y′′−5y′+4y=0 мы сначала найдем характеристическое уравнение, которое имеет вид:

\ [y (t) = C_1 e^ {4t} + C_2 e^ {t} \],

где \ (C_1\) и \ (C_2\) — произвольные константы, которые определяются начальными условиями.

Ответы к ЗАДАНИЯМ