Бесплатный фрагмент - Математика для DATA SCIENTIST

Математика (Математическое обучение) для DATA SCIENTIST

Предисловие

Когда спрашивают — зачем DATA SCIENTIST’у дифференциальные уравнения, можно вспомнить графики Курта Воннегута в координатах (время по оси Х, уровень счастья-несчастья по оси Y).

https://www.youtube.com/watch?v=EEL-PIZVO08

Например, постепенное затухание жизненных сил описывается кратко и понятно одной формулой exp (-k* t), которую сразу видно на графике, где t — время, а что может быть понятнее этой переменной? Или атомный взрыв- той же экспонентой, только с положительным аргументом exp (k*t), качания на качелях или супружескую эмоциональную жизнь — одним уравнением x’' = — k*x. И траекторией y= sin (t). Как тут не вспомнить один из лучших учебников по Микроэкономике Вэриана, где автор долго и добросовестно уговаривает американцев выучить производные, чтобы одной строчкой записывать то, что иначе надо на целую страницу разъяснять.

Совсем недавно мне нужно было консультировать магистерскую диссертацию по «Применение DATA SCIENCE в классификации архетипов американских киносценариев», там была взята за основу тройка хэппи-ендов и тройка трагедий в тех же координатах, что и у Курта Воннегута.

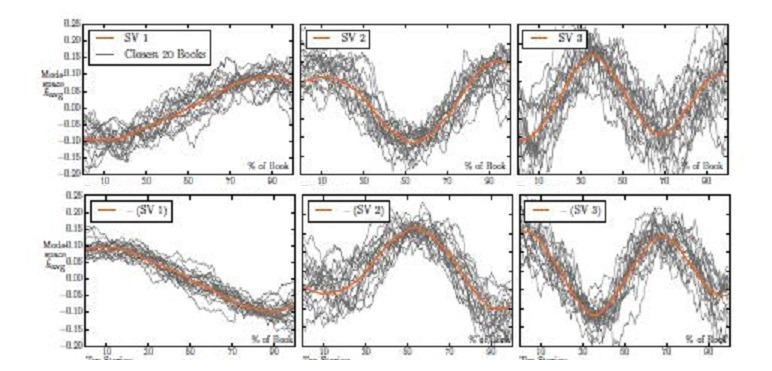
Теперь давайте предположим, что у нас есть случайная величина Z по всему сценарию как оценка (счастья-несчастья) в данный момент времени t. Ну и соответственно выборка Z (n). Как нам найти главного героя? Если есть только реплики? Я предложил ввести аналогичные Х1 (t), X2 (t) и т. д. Конечно, чтобы определить главного героя DATA SCIENCE будем вычислять ковариацию и/или корреляцию corr (Z, Xi). То есть достаточно всего одного числа — по выборке. А как определить врага главного героя? Надо искать отрицательную максимальную корреляцию. А если корреляция близка к нолю? Это кто, как вы думаете, Уважаемый Читатель? Вот вам и потребность в Теории вероятностей и Корреляционном анализе для DATA SCIENTIST.

Иногда также сомневаются в нужности Векторной алгебры и даже матриц, но это снимается теми соображениями, что бальшие массивы данных частно необходимо делить на блоки с малыми связями, как бы нарезать подмножества из всего большого множества. А также уметь смотреть под разными углами или с разных точек зрения. Но ведь это не что иное, как замена базиса пространства и определение ортогональных подпространств меньшей размерности. Вообще говоря, Линейная алгебра — должна быть в преподавании доведена до максимальной степени простоты и это только улучшает ее понимание учащимися.

Что касается предмета «Математический анализ бесконечно малых переменных величин», то мне трудно представить начинающего DATA SCIENTISTa, кто бы сомневался в необходимости этого фундаментального раздела высшей математики.

1. Алгебра

1.1 Комплексные числа. Геометрическое представление, алгебраическая и тригонометрическая форма записи, извлечение корней, корни из минус единицы.

1.2 Метод Жордано-Гаусса к системам линейных уравнений. Прямоугольные матрицы как способ представления систем линейных уравнений. Приведение матриц и систем линейных уравнений к ступенчатому виду. Самый простой и надежный метод.

1.3 Ранг матрицы. Линейная зависимость строк (столбцов). Основная лемма о линейной зависимости, базис и ранг системы строк (столбцов). Ранг матрицы. Критерий совместимости и определенности системы линейных уравнений в терминах рангов матриц. Фундаментальная система решений однородной системы линейных уравнений.

1.4 Определители. Определитель квадратной матрицы, его основные свойства. Критерий равенства определителя нулю. Формула разложения определителя матрицы по строке (столбцу). Самый простой и надежный метод.

1.5 Операции над матрицами. Операции над матрицами и их свойства. Теорема о ранге произведения двух матриц. Определитель произведения двух квадратных матриц. Обратная матрица, ее явный вид (формула), способ выражения с помощью элементарных преобразований строк. Самый простой и надежный метод.

1.6 Вектора, векторные пространства. Векторное пространство, его базис и размерность. Преобразование координат в векторном пространстве. Подпространства как множество решений систем однородных линейных уравнений Связь между размерностями суммы и пересечения двух подпространств.

1.7 Линейные отображения и линейные операторы. Линейные отображения, их запись в координатах образ и ядро линейного отображения, связь между их размерностями. Сопряженное пространство и сопряженные базисы. Изменение матрицы линейного оператора при переходе к другому базису.

1.8 Билинейные и квадратичные функции. Билинейные функции, их запись в координатах. Изменение матрицы билинейной функции при переходе к другому базису. Ортогональное дополнение к подпространству относительно симметрической билинейной функции. Связь между симметрическими билинейными и квадратичными функциями. Существование ортогонального базиса для симметрической билинейной функции. Нормальный вид вещественной квадратичной функции. Закон инерции.

1.9 Евклидовы пространства. Неравенство Коши-Буняковского. Ортогональные базисы. Ортогонализация Грама-Шмидта. Ортогональные операторы.

1.10 Собственные векторы и собственные значения. Собственные векторы и собственные значения линейного оператора. Собственные подпространства линейного оператора, их линейная независимость. Условие диагонализируемости оператора.

Литература.

— Беклемишев Д. В. Курс аналитической геометрии и линейной алгебры. М. ФИЗМАТЛИТ, 2005. — 304 с.

— Кострикин А. И. Введение алгебру, ч. I, II, 2000, Физмат. лит.

— Курош А. Г. Курс высшей алгебры. 1975, Наука.

— Сборник задач по алгебре под редакцией Кострикина А. И. / И. В. Аржанцев, В. А. Артамонов, Ю. А. Бахтурин и др. — МЦНМО Москва, 2009.

Для заметок по ссылкам на ресурсы в интернете и на задачи и/или на другие ресурсы (в печатной версии)