
Предисловие
Нет сомнений: вселенная бесконечна.
Эпикур
Развитие физических наук вместе со всеми её аспектами, приводит к необходимости развития его математического аппарата, также и приводя к необходимости разрешения уже математических проблем и нахождения процесса их решения. И одной из таких проблем является решение уравнений, связанных с делением на ноль, но как оказалось, эта проблема становиться более обширной и приводит к образованию даже настоящего нового вида чисел. В данной работе рассмотрен вопрос самого определения двух разновидностей новых чисел, получивших своё название из латинского языка как ингенциальные и пер-ингенциальные числа, которые могут при вводе их в математический аппарат привести к большим успехам и указать новые горизонты в различных исследованиях, что и доказывает их актуальность. Вместе с этим важно отметить возможность их применения в самых различных областях науки и техники приводя к новым результатам.
На сегодняшний день опубликовано несколько научных статей на данную тему и проведены расчёты, но подробных исследований в этой области не было замечено и не было проведено, благодаря чему это исследование является единственной в своём роде работой за всю историю математики, где рассматривался бы этот её новый раздел.
Говоря о базе образования этих чисел, можно сказать, что она была выработана из комплексных чисел. И если обращаться к истории комплексной математики, то необходимо вспомнить труды знаменитого Кардано «Великое искусство, или об алгебраических правилах» 1545 года, где он при решении квадратного уравнения получил отрицательное число под корнем. Также уже после работ Бомбелли 1572 года уже стало известны о возможности использования комплексных чисел при решении кубических уравнений различных разновидностей.
Но комплексные числа в основном помогли определить сам алгоритм процесса математического описания данных чисел, ибо сами по себе некогда являлись невообразимыми и лишь после представления их в решении уравнения Шрёдингера для описания действительных элементарных частиц, стали частью науки как действительно существующие в природе.
Переходя же к уравнениям связанные с делением на ноль, то эти уравнения встречались во многих случаях и всегда указывались как не имеющие решения, но как показывают сегодняшний исследования они действительно существуют. Так, по некоторым результатам данной работы, эти числа могут быть сравнимы по своей важности и неординарности с кватернионами и иными высокими степенями нестандартных в математике чисел.
Целью данного исследования является полноценное определение понятия ингенциальных и пер-ингенциальных чисел, после процесса исследования релятивистской функции, а также определение местоположения на числовой оси. Вместе с этим определение арифметических и алгебраических операций над этими числами, участие их в различных теориях, указание различных операций над ними до некоторого определённого уровня первоначальной математики. Далее уже следует переход на последующий этап исследования.
Задачи исследования являются:
· Определение первоначальных понятий числа и его разновидностей;
· Представление операций с различными видами чисел;
· Исследование релятивистской функции с указанием последующих выводов;
· Указание понятия ингенциальных чисел и определение их местонахождения на числовой оси;
· Изучение процессов проведения алгебраических и арифметических операций с ингенциальными числами;
· Представление роли ингенциальных чисел в тригонометрическом представлений;
· Решение уравнения Эйлера с ингенциальными числами;
· Указание геометрического смысла ингенциальных чисел;
· Определение местонахождения комплексных чисел на числовой оси;
· Указание понятия пер-ингенциальных чисел и определение их местонахождения на числовой оси;
· Изучение процессов проведения алгебраических и арифметических операций с пер-ингенциальными числами;
· Представление роли пер-ингенциальных чисел в тригонометрическом представлений;
· Решение уравнения Эйлера с пер-ингенциальными числами;
· Указание геометрического смысла пер-ингенциальных чисел.
Объектом данного исследования являются ингенциальные и пер-ингенциальные числа.
Предметом исследования является процесс определения всевозможных операций в ингенциальной математике.
При проведении данной работы применён теоретический метод исследования.
Научная новизна данной работы заключается в следующем:
· Первое исследование функции для релятивистской энергии как полностью математический объект;
· Определение местонахождения на числовой оси комплексных чисел;
· Первое указание понятия ингенциальных чисел и определение их местонахождения на числовой оси;
· Изучение процессов проведения алгебраических и арифметических операций с ингенциальными числами;
· Представление роли ингенциальных чисел в тригонометрическом представлений;
· Решение уравнения Эйлера с ингенциальными числами;
· Указание геометрического смысла ингенциальных чисел;
· Первое определение местонахождения комплексных чисел на числовой оси;
· Указание понятия пер-ингенциальных чисел и определение их местонахождения на числовой оси;
· Изучение процессов проведения алгебраических и арифметических операций с пер-ингенциальными числами;
· Представление роли пер-ингенциальных чисел в тригонометрическом представлений;
· Решение уравнения Эйлера с пер-ингенциальными числами;
· Указание геометрического смысла пер-ингенциальных чисел.
Практические результаты заключаются в следующем:
· Положен новый этап в развитии математического аппарата запутанных квантовых состояний;
· Открыта возможность решения уравнений Шрёдингера и иных уравнений, связанных с комплексными числами, благодаря ингенциальным операциям;
· Полное или частичное выполнение функций комплексных чисел ингенциальными выражениями и операциями.
Достоверность результатов основана на чисто математическом представлении данной операции с последующими составляющими и выводами, благодаря чему не подлежит какому-либо сомнению.
Говоря о значимости данного исследования, то уместно отметить тот факт, что при использовании данной математики в широком спектре, это может привести к созданию целого ряда самых различных удобств при решении задач, выполнении многочисленных функций и прочих.
Данное исследование было обсуждено на собрании учёных Научной школы «Электрон», при Организации «Электрон» и созданный совместно с Ферганским Государственным Университетом. Также данный проект является одним из первых проектов, активно развивающихся в стенах новой Научной школы, и порождает целый ряд направлений для новых исследований.
Таки образом, можно сказать, что проект «Ингенциальной математики» уже делает свои первые шаги в направлении успеха и своего развития, порождая новые направления и многообещающие результаты, которые с большой вероятностью могут оказаться настоящим прорывом в науке!
Бурнашев Марат Альбертович
Ибратжон Хатамович Алиев
Раздел 1. Теоретические выкладки
Глава 1. Понятие числа
Перед тем начать само исследование, важно остановится на нескольких основных понятиях и первым из них, конечно же является само «число». Число – это одно из основных понятий в математике, которое используется для количественной характеристики, сравнения, нумерации объектов и их частей. Для их обозначения используются цифры, а также символы различных математических операций. Сами числа возникли в первобытном обществе из необходимости к счёту, но с развитием науки значение этого термина конечно же расширилось.
Останавливаясь на этом понятии, нельзя не остановиться на основных множествах чисел, которые активно применяются в счёте и проведении различных операций, но в последующих главах некоторые из этих множеств будут рассмотрены уже более подробно со всеми свойствами.
Первым множеством является множество натуральные числа – это числа, получаемые при естественном счёте, обозначаясь через N. При этом натуральные числа являются замкнутыми относительно сложения и умножения. А сложение и умножение натуральных чисел коммутативно и ассоциативно, также умножение натуральных чисел дистрибутивно относительно сложения и вычитания.
Второй множество – множество целых чисел состоит из чисел получаемые при объединении множества натуральных чисел с множеством чисел противоположных натуральным и нулём, обозначаются как Z. Любое целое число можно представить как разность двух натуральных. Целые числа замкнуты относительно сложения, вычитания и умножения. Также это множество является кольцом.
Третье множество – множество рациональных чисел, обозначаемых через Q, представляют собой числа, представимые в виде дроби m/n, где числитель – целое число, а знаменатель – натуральное. Рациональные числа замкнуты уже относительно всех четырёх арифметических действий: сложения, вычитания, умножения и деления (кроме деления на ноль, эта операция уже принадлежит ингенциальному множеству); такое множестве или точнее алгебраическая структура является полем.
Четвёртое множество – действительные или вещественные числа, обозначаемые через R, это числа, представляющий собой расширение множества рациональных чисел, замкнутое относительно некоторых операций предельного перехода. Множество вещественных чисел обозначаются через R. Его можно рассматривать как пополнение поля рациональных чисел Q при помощи нормы, являющейся обычной абсолютной величиной. Кроме рациональных чисел, это множество также включает в себя множество иррациональных чисел I, не представимых в виде отношения целых.
И наконец, одно из самых известных на сегодня множеств, пятое множество – комплексное множество C, состоящее из чисел, являющиеся расширением множества действительных чисел. Они могут быть представлены через вещественную и комплексные части, с участием мнимой единицы, которая в чётных степенях даёт -1. Комплексные числа подразделяются на алгебраические и трансцендентные. При этом каждое действительное трансцендентное является иррациональным, а каждое рациональное число – действительным алгебраическим. Более общими классами чисел, чем алгебраические, являются периоды – числа, выражающие объём в n-мерном пространстве, вычислимые – число выводимое при помощи заданного алгоритма с сколь угодной точностью и арифметические числа – множество натуральных чисел, определяющиеся формулой первой степени.
Но перед тем, как будет совершён переход на следующий этап, важно несколько остановится на некотором из данных множеств.
Углубляясь в историю древних цивилизаций, можно сделать вывод что с древних времен люди ввели систему счета. В первобытные времена как можно догадаться уровень развитости людей на планете был на низшем уровне, несмотря на это они учились выживать в те суровые времена, учились охотиться, добывать еду. По древним рисункам на скалах, которые археологи находят посей день, можно сделать вывод, что система счета была неприемлемой частью жизни того народа.
Они считали: сколько (добычи) было собранно, сколько можно сегодня израсходовать, а сколько оставить до конца следующей охоты. Следовательно, множество натуральных чисел – это числа, используемые при счете. Обозначение их, как и было указано – N, и входят в это множество числа от {1,2,3,4… до бесконечности}. Множество натуральных чисел занимает первый ряд среди всех множеств чисел. Над натуральными числами можно проводить несколько арифметических операций:
Сложение (1.1):
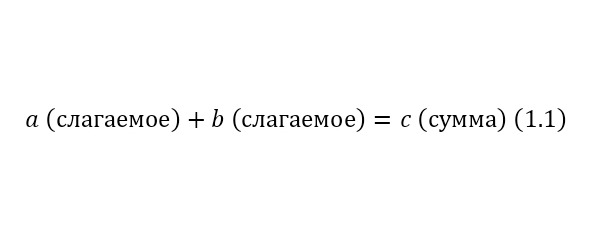
Умножение (1.2):
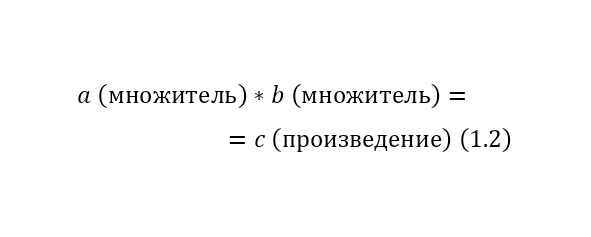
Вычитание (1.3):
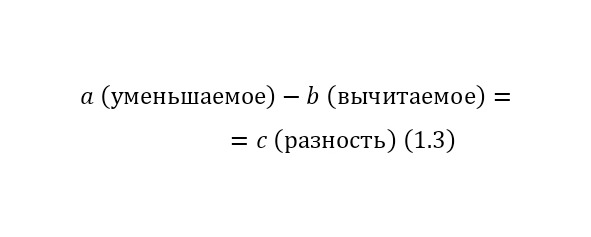
При этом уменьшаемое должно быть больше вычитаемого, иначе в результате получится отрицательное число или ноль, то есть число уже не будет принадлежать множеству натуральных чисел;
Деление (1.4):

Деление с остатком (1.5):
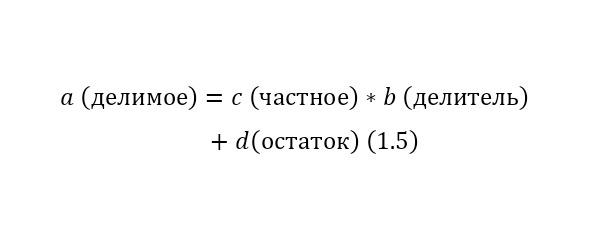
При этом сложение и умножение коммутативны и ассоциативны. А умножение дистрибутивно на сложении и вычитании.
Также можно перечислить и некоторые алгебраические операции:
Возведение в степень (1.6):

Также важно знать, что натуральные числа пишутся в ряд по возростанию.1, 2, 3, 4, 5, 6, 7 и т. д. Наименьшее натурально число – единица (1).
Класс – группа из трех цифр, на который разбито число, начиная справа. Последний класс может состоять из трех, двух или одной цифры. Первый класс – класс единиц; второй класс – класс тысяч; третий класс – класс миллионов; четвертый класс – класс миллиардов; пятый класс – класс триллионов; шестой класс – класс квадрильонов (квадриллионов); седьмой класс – класс квинтильонов (квинтиллионов); восьмой класс – класс секстильонов; девятый класс – класс септильонов и т.д.
Также имеют место числа вида:
1) Четные числа – это те числа, которые оканчиваются цифрами 0; 2; 4; 6; 8, то есть числа, которые делятся на 2 без остатка;
2) Нечетные числа – это те числа, которые оканчиваются цифрами 1; 3; 5; 7; 9 – числа не кратные 2.
Также по своей разновидности они делятся на 2 вида:
1) Простые числа – это натуральные числа, имеющие только два положительных делителя.
2) Составное число – это натуральное число, имеющее более двух положительных делителей.
Любое число, является либо простым, либо составным.
Целые числа – это натуральные числа, числа, противоположные им, и число нуль. Множество целых чисел обозначается буквой Z. Множество натуральных чисел входит в множество целых чисел, то есть является его подмножеством. Целые числа лежат на промежутке: (-∞; 0), то есть например: числа -1, -18, 0 – являются целыми. Над целыми числами можно проводить несколько алгебраических операций:
1) Сложение. Для того, чтобы сложить два целых числа с разными знаками, нужно из модуля большего числа вычесть модуль меньшего и перед результатом поставить знак большего по модулю числа.
2) Вычитание. Вычитание целых чисел сводится к сложению уменьшаемого и числа, противоположному вычитаемому.
3) Умножение. Для того, чтобы перемножить два целых числа, нужно перемножить их модули и перед произведением поставить знак плюс, если исходные числа были одного знака, и минус – если разного.
4) Деление. Для того, чтобы разделить одно целое число на другое, нужно разделить модуль первого числа на модуль второго и поставить перед частным знак плюс, если знаки делимого и делителя одинаковые, и минус, - если разные.
Целые числа делятся на 2 вида: положительные и отрицательные. Положительные целые числа – это целые числа больше нуля. Например, число 67 – целое число со знаком плюс, то есть положительное целое число большее нуля. На координатной прямой это число лежит справа от точки отсчета, за которую принято число 0. Другие примеры положительных целых чисел: 76,509, 87, 33, 12, 657.
Отрицательные целые числа – это целые числа меньшие нуля. Примеры целых отрицательных чисел: −987, −234, −1. Но стоит отметить, что само число (0) является не отрицательным и не положительным.
Любое число, противоположное положительному целому числу, в силу определения, является отрицательным целым числом. Справедливо и обратное. Число, обратное любому отрицательному целому числу, есть положительное целое число. Таким образом мы выяснили что (1.7).
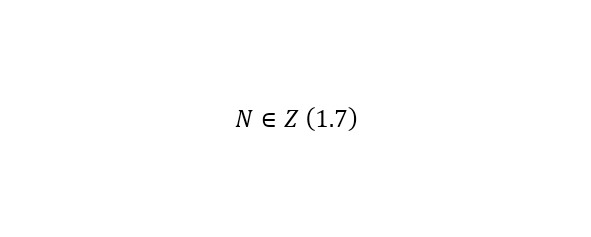
Рациональные числа – числа представимые в виде дроби k/m, где m≠ 0 и k – целое число, а m – натуральное число. Над рациональными числами можно проводить арифметические действия такие как: сложение, вычитание, умножение и деление (кроме деления на ноль). Обозначаются множество рациональных чисел буквой Q. Исходя из вышеперечисленных множеств можно сделать вывод что множество рациональных чисел охватывает два множества: натуральные и целые, то есть (1.8).
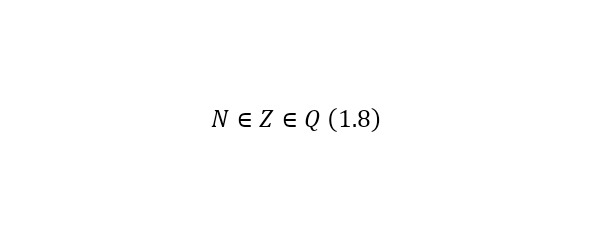
Действительные числа – числа, представляющие собой расширенное множество рациональных чисел относительно некоторых (важных для математического анализа) операций предельного перехода. Обозначаются действительные числа буквой (R), следовательно, (1.9).
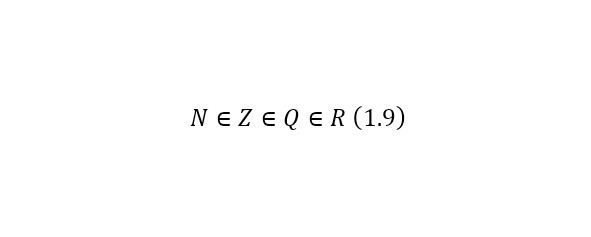
Комплексные числа – аналогично являются расширенным множеством действительных чисел. Они могут быть записаны в виде (1.10), где i – мнимая единица, для которой справедливо равенство (1.11).
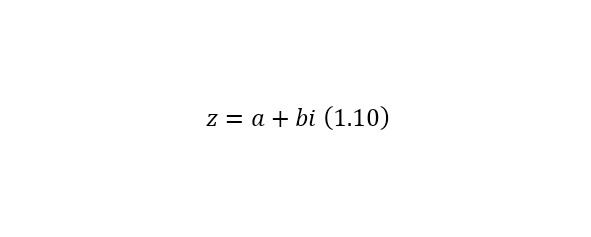
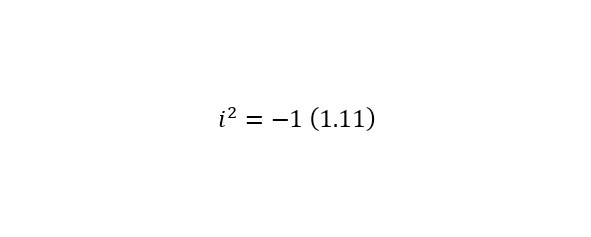
Комплексные числа используются в квантовой механике, в теории хаоса, гидродинамике, теории упругости и т. д. Комплексные числа разделяются на 2 вида: алгебраические и трансцендентные. При этом каждое действительное трансцендентное является иррациональным, а каждое рациональное число — действительным алгебраическим. Обозначаются комплексные числа буквой C. На сегодняшний день комплексные числа являлись вершиной всех множеств, следовательно (1.12).
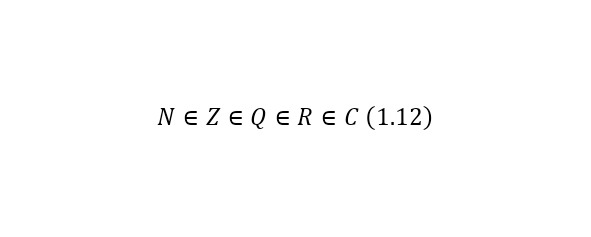
В дальнейшем этапе важно остановиться подробнее именно на комплексном множестве, после чего можно переходить уже началу исследования.
Глава 2. Комплексные числа
Комплексные числа, от латинского complexus – связь, сочетания, о двойном ударении — числа общего вида (2.1—2.2).

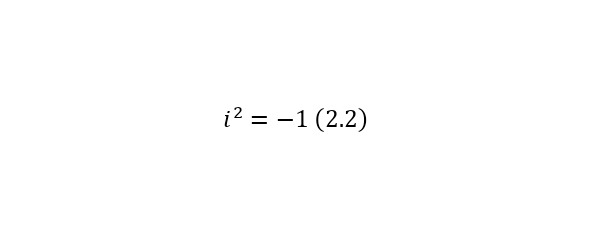
Множество комплексных чисел обозначается через C, а все действительные числа, можно рассматривать как частный случай комплексных, они имеют вид (2.3).
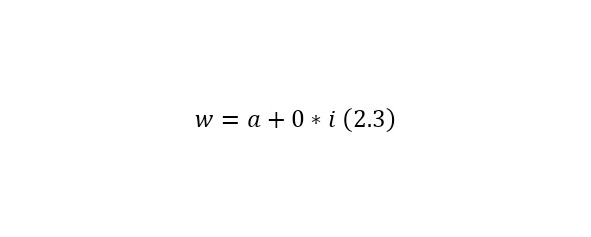
Также как и для вещественных чисел, для комплексных определены операции сложения, вычитания, умножения и деления. Однако некоторые их свойства отличны, о чём подробно будет указано далее. Также комплексные числа обладают геометрическим представлением на комплексной плоскости, благодаря необходимым отклонениям. Но перед тем, как углубиться, необходимо осознать вводимые операции.
Для начала необходимо исследовать это понятие и в первую очередь из этого значения вытекает, что число i удовлетворяет равенству (2.4).
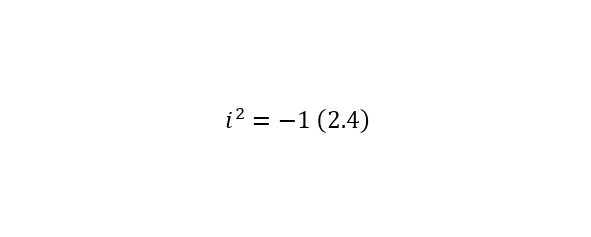
То есть это число единственное из всех существующих, которое бы возведении во вторую степень будет равняться минус единице. Следовательно оно также является решением уравнений указанных в (2.5).
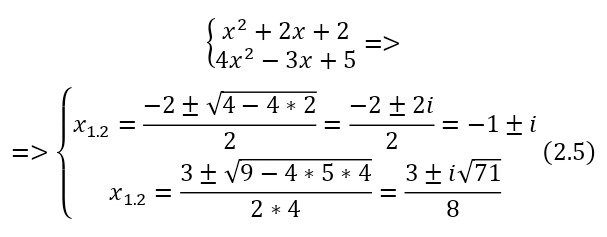
Это утверждение возникает сразу из логического доказательства (2.6).
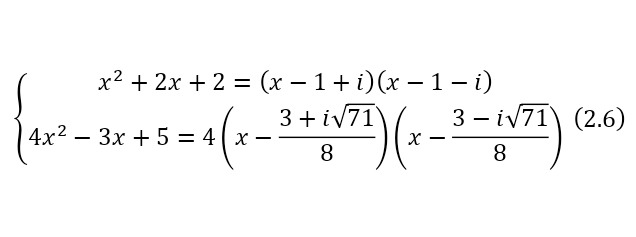
Также ещё одним доказательством к этому утверждению является (2.7).
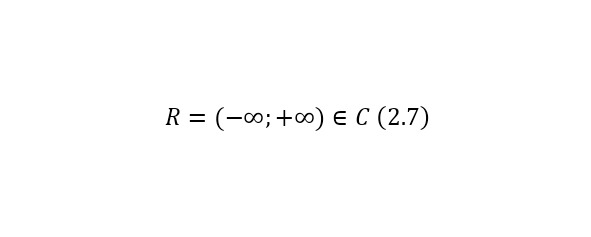
Под бесконечностью здесь понимаются все числа входящие во множество действительных чисел, то есть чисел вида (2.8), если же мнимая часть в этом случае равняется нулю, то это значение уже принадлежит множеству действительных чисел, далее уже следует иерархия (2.9).
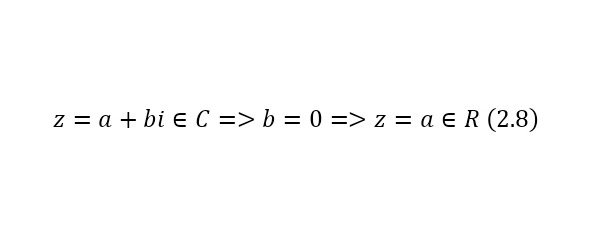
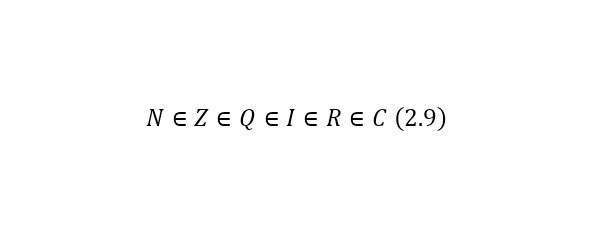
Где уместно указать в качестве C, множество всех комплексных чисел, для которых также уместно ввести общий вид (2.10).
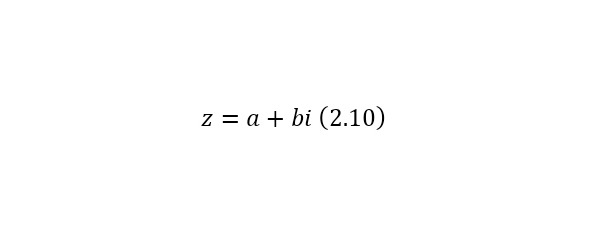
Говоря об общем виде комплексного числа, то можно указать, что и оно является решением для первого уравнения в (2.5).
Наконец, когда был выведен общий вид комплексного уравнения, то уже можно указать, что первое слагаемое в этом случае является вещественной частью, а второе — мнимой частью, при этом если обе постоянные являются вещественными числами, то при обнулении вещественной части, само число считается чисто комплексным, а в случае обнуления второй постоянной — вещественным числом.
Противоположным для некоторого числа (2.11) будет его вид в том же (2.11).
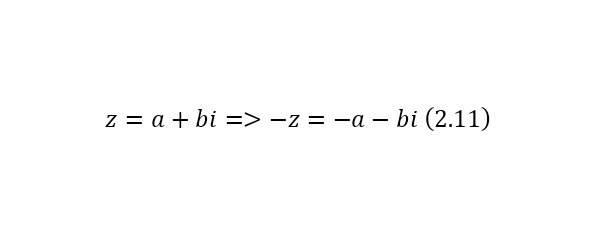
Комплексные числа, не подлежат сравнению, но равными считаются лишь комплексные числа вещественные и мнимые части которых равны (2.12).
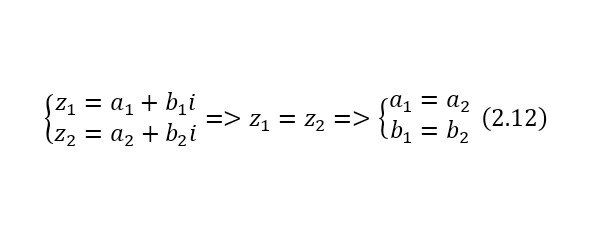
Для каждого комплексного числа, вместе с этим определены арифметические операции, которые описываются далее. Определение сложения и вычитания комплексных чисел представлены в (2.13—2.14).
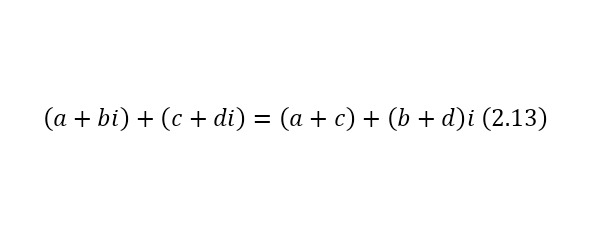
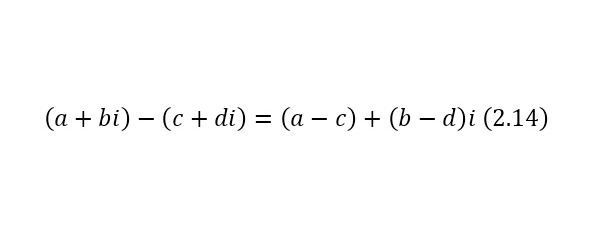
Вместе с этим, для комплексных чисел справедливы 5 свойств. Свойство коммутативности или переместительное свойство (2.15).
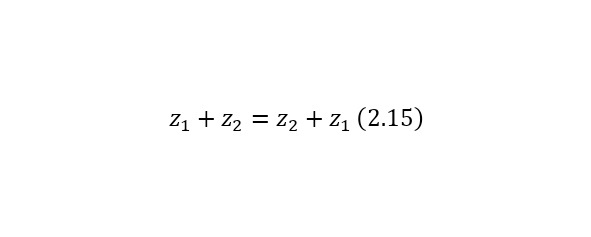
Свойство ассоциативности или сочетательное свойство (2.16).
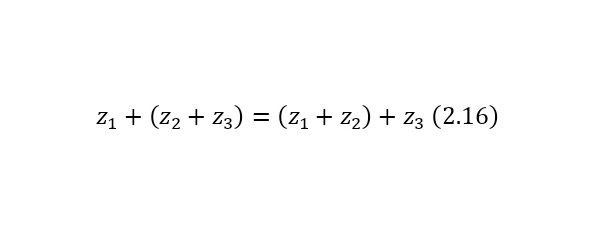
Свойство нуля (2.17).
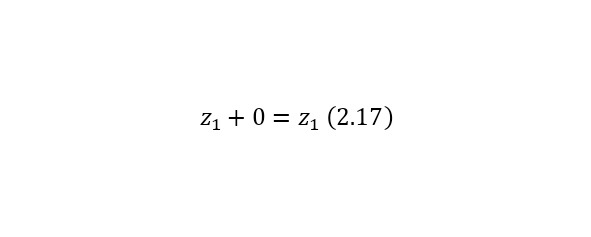
Свойство противоположного элемента (2.18).
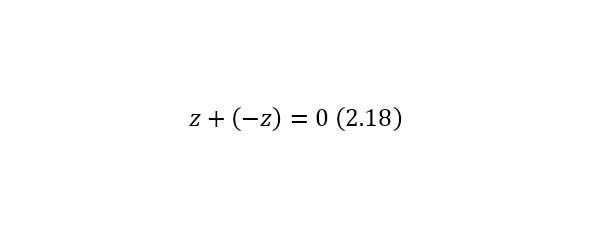
Выполнение вычитания через сложение (2.19).
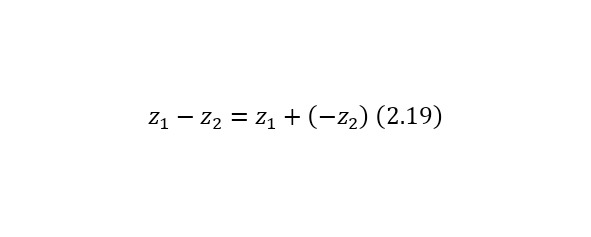
Произведение двух комплексных чисел можно определить в (2.20).
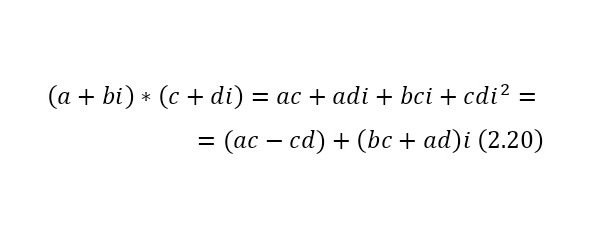
Операция нахождения произведения же обладает свойствами коммутативности (2.21), ассоциативности (2.22), свойством единицы (2.23), свойством нуля (2.24), а также дистрибутивностью (2.25).
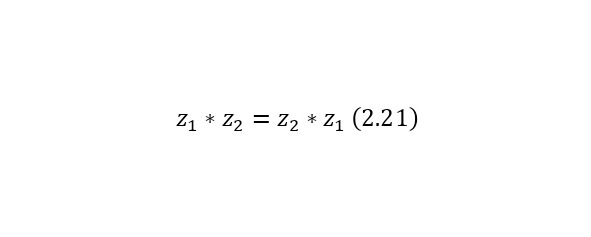
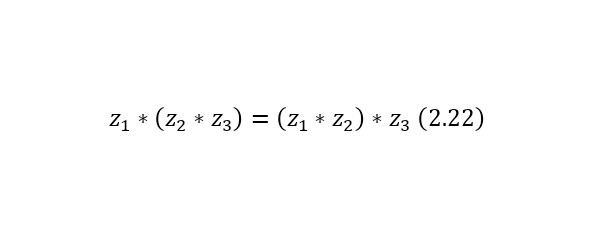
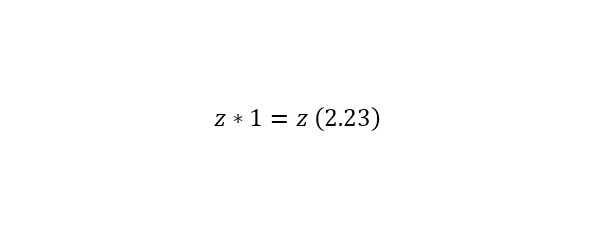
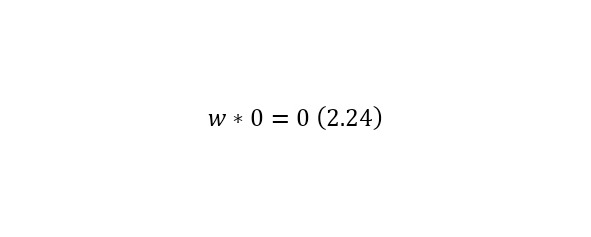
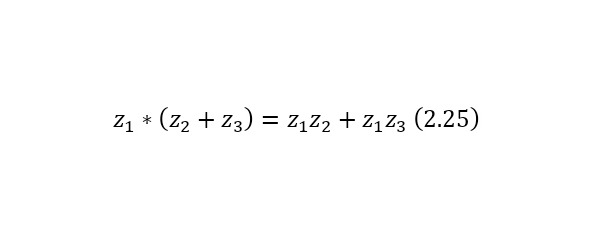
Правило же для натуральных степеней комплексной единицы определяется по (2.26), а обратных также по (2.26).
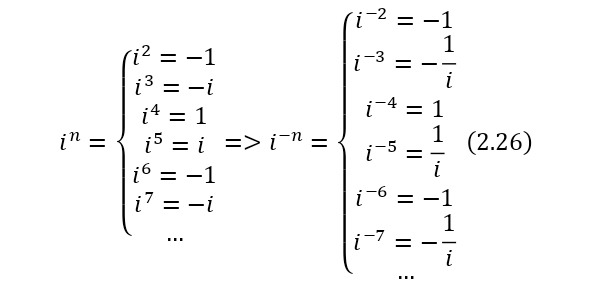
После определения операций с комплексными числами, общая запись комплексного числа можно воспринимать не как формальную запись, а как выражение, составленное по приведённым выше законам сложения и умножения. То есть общую запись можно представить как (2.27).
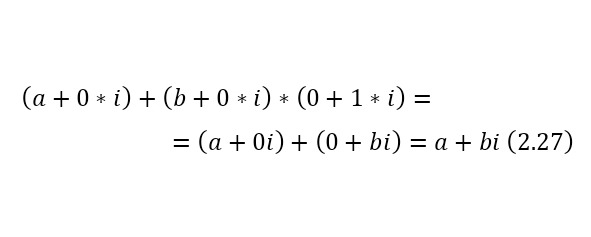
Некоторое комплексное число (2.28) будет сопряжённым для (2.29), таким образом для любого комплексного числа, кроме нуля, можно найти обратное к нему комплексное число через (2.30).
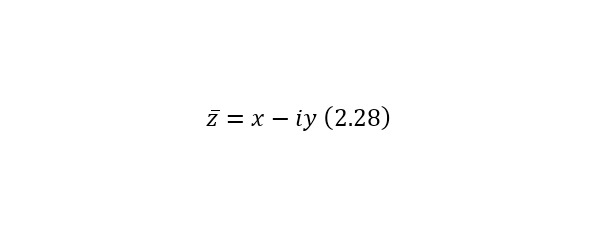
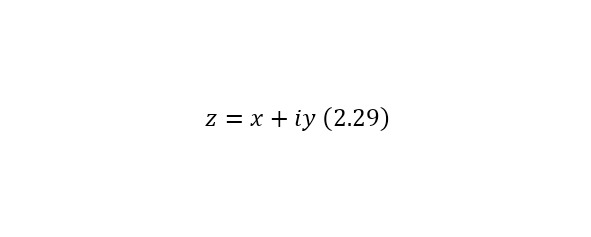
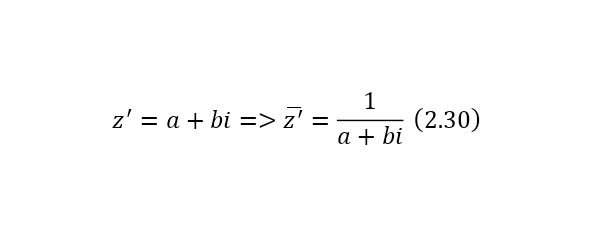
Теперь же можно определить результат деления одного комплексного числа на второе (2.31).
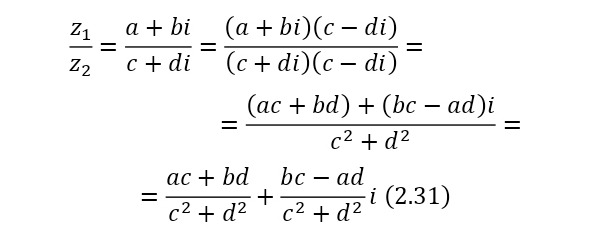
При этом также деление можно заменить умножением делимого на число, обратное делителю. Для комплексных чисел определены также операции извлечения из корня мнимой единицы (2.32), возведение в степень (2.33) и наконец, операцию извлечения из корня общего вида (2.34).
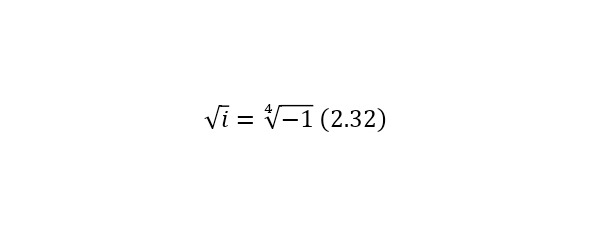
Для нахождения формулы возведения в степень комплексного числа необходимо исходить из последовательности, которая приводит к общему виду в (2.33) через биноминальное выражение.
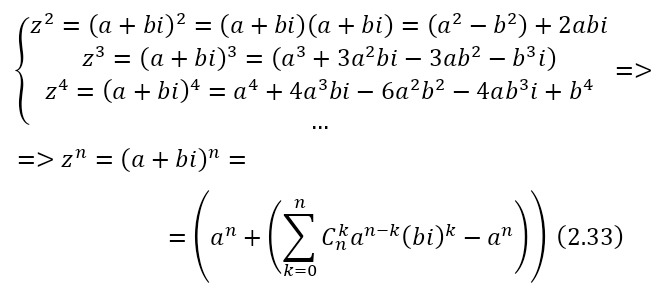
После того как операция возведения в n-ую степень определена, сделать обратную операцию не составит труда, ибо это приведёт к образованию системы, решив которую остаётся лишь подставить результат (2.34).
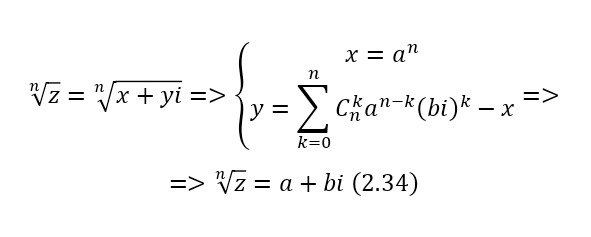
Также интересно решение уравнения Эйлера с ингенциальной единицей, а после и с общим видом ингенциального числа, что и описывалось далее, приняв выражения как неизвестные. И для этого изначально можно исходить из разложений Тейлора (2.35—2.37).
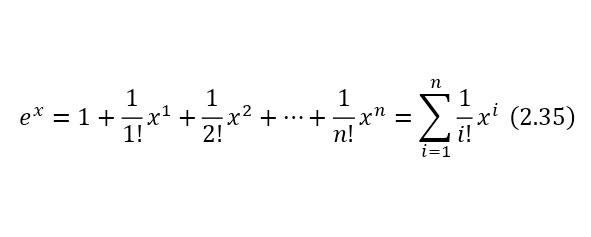
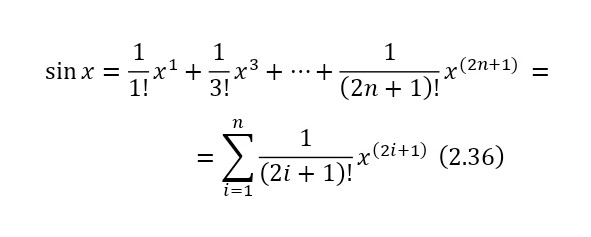
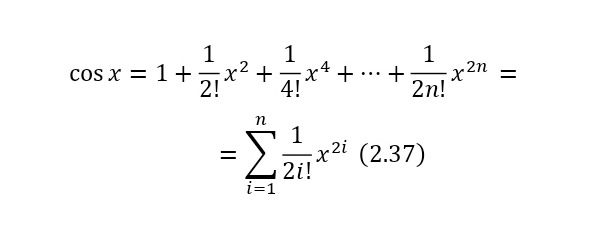
Что легко доказывается, поскольку при обнулении неизвестной синус в (2.36) также обнуляется, а косинус в (2.37) равняется единице. И уже из этого вытекает (2.38).
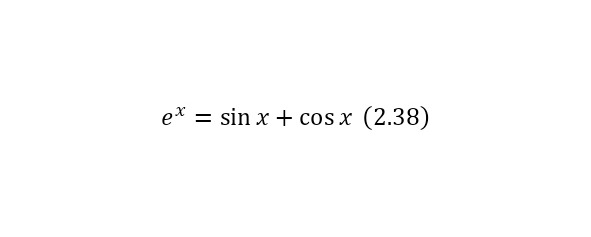
И неизвестным в (2.38) могут быть все возможные числа, как комплексные, при подстановке которых вытекает замечательное равенство Эйлера (2.39).
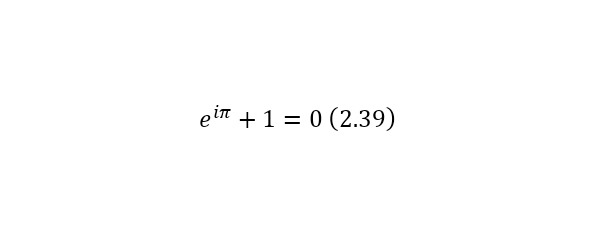
Комплексные числа можно выразить на комплексной плоскости. У этой системы координат в качестве ординаты находится ось, начинаемая от нуля с мнимым множителем, а у абсциссы — все действительные числа. Таким образом все комплексные числа можно представить на такой прямоугольной системе координат.
В такой системе числу (2.40) соответствует своя координата и радиус-вектор, соединяющий начало координат с этой точкой.
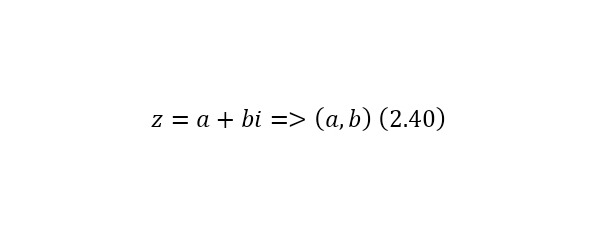
Такая плоскость, как и было указано называется комплексной. И благодаря расположению каждого вида чисел, каждая ось называется вещественной и комплексной осью. Удобно рассматривать на комплексной плоскости также полярную плоскость или систему координат, в которой координатами точки являются модули расстояния до начала координат и угол радиус-вектора точки с горизонтальной осью. То есть координата на вещественной оси представляет собой произведение косинуса угла радиус-вектора на модуль самого вектора, а на ингенциальной оси — синуса этого же угла и модуля того же радиус-вектора.
В этом представлении сумма комплексных чисел соответствует векторной сумме соответствующих радиус-векторов, а вычитанию — вычитание радиус-векторов. При нахождении их произведения их модули перемножаются, а аргументы складываются, что выводится либо из тригонометрических формул суммы, либо из формулы Эйлера. Если же модуль второго сомножителя равен 1, то умножение на него соответствует повороту радиус-вектора первого числа на угол, равный аргументу второго числа.
Модулем комплексного числа называется длина радиус-вектора соответствующей точки комплексной плоскости. Модуль для комплексного числа со своим обозначением представляется в (2.41).
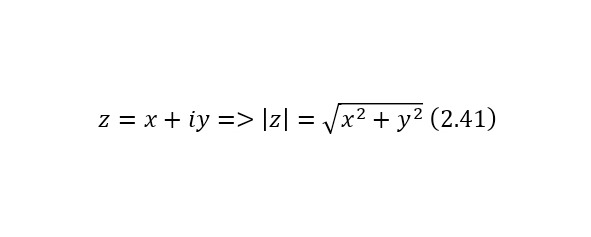
Для любых комплексных чисел соответствуют следующие свойства модуля (2.42—2.46).
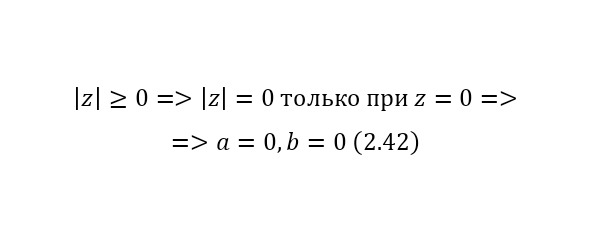
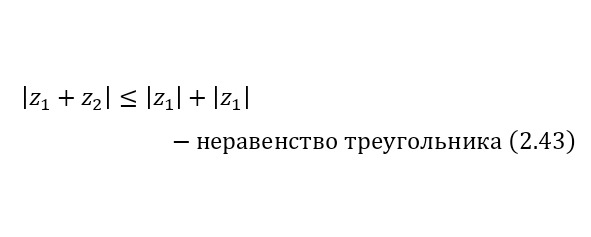
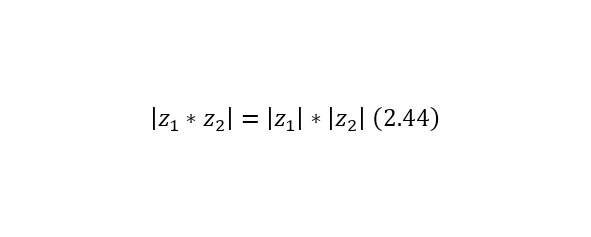
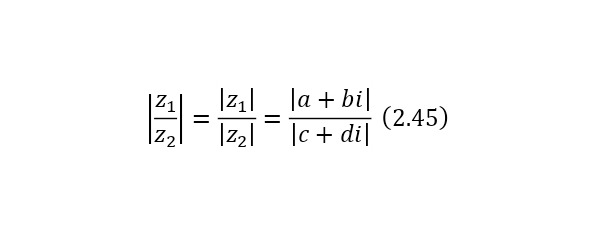
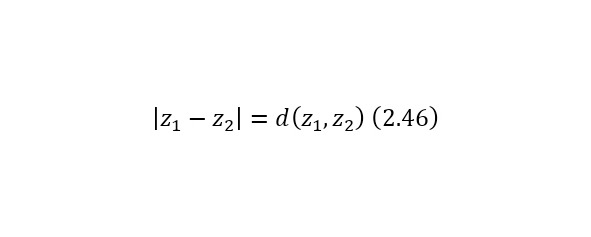
Аргументом ненулевого комплексного числа называется угол между радиус-вектором соответствующей точки и положительной вещественной полуосью. Аргумент комплексного числа измеряется в радианах, обозначается и определяется по (2.47).
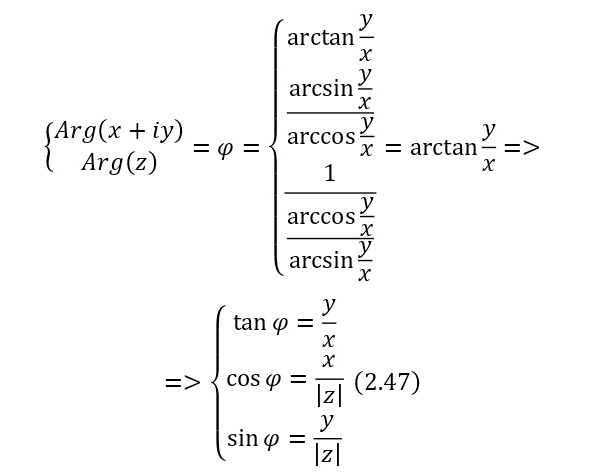
Для комплексной единицы и её производных, то есть, когда второй аргумент равен единице или иному вещественному числу, а первый уже обнуляется, аргумент является комплексным арктангенсом. В случае полного комплексного числа значение угла определяется с точностью до полупериода.
Сам аргумент обладает некоторыми свойствами, первым из которых является свойства о том, что аргумент обратного числа отличается знаком от аргумента исходного комплексного числа (2.48).
Бесплатный фрагмент закончился.
Купите книгу, чтобы продолжить чтение.