Бесплатный фрагмент - Информационные технологии в управлении

Введение

В данном пособии приводятся примеры использования аналитической платформы «Deductor». Рассматриваются некоторые возможные реализации нейронных сетей, кластеризация с помощью карт Кохонена, прогнозирование временных рядов и создание баз знаний.

Наличие достаточно развитых инструментальных программных средств аналитической платформы «Deductor» позволяет аналитику при построении модели прогнозируемого процесса руководствоваться такими понятиями, как опыт и интуиция. В ряде случаев, когда нет необходимости в строгой математической спецификации модели, такой подход представляется вполне допустимым, что особенно ценно при анализе плохо формализуемых процессов.

Изучение пособия дает возможность студентам бакалавриата и магистратуры существенно продвинуться в освоении совокупности методов и средств аналитической обработки информации.

Пособие предназначено для студентов факультета государственного управления МГУ, а также студентов гуманитарных специальностей, изучающих информационные технологии в управлении.

Хочу выразить свою благодарность доценту Кафедры математических методов и информационных технологий Факультета государственного управления МГУ И.А.Смольниковой за оказанную помощь и полезные советы при редактировании этой книги.

Если у Вас возникнут вопросы, то пишите мне dudikhin@yandex.ru

I. Аналитическая платформа Deductor

Аналитическая платформа платформа Deductor — это отечественный программный продукт, разработанный компанией BaseGroup Labs. С его помощью возможно решение самого широкого спектра задач, начиная от создания систем корпоративной отчетности и до решения задач Data Mining.

Это специализированное программное решение выполнено на базе единой платформы и содержит в себе необходимые инструменты для извлечения закономерностей из «сырых» данных. Оно позволяет пройти все этапы построения аналитической системы: от создания хранилища данных до автоматического подбора моделей и визуализации полученных результатов.

Система позволяет анализировать любые табличные данные и для решения аналитических задач. В ней предусмотрена возможность использования следующих специальных технологий:

— Data Warehouse (хранилища данных) — консолидация данных и обеспечение быстрого и понятного для аналитика доступа к ним

— OLAP (многомерный анализ) — визуализация, отчетность и удобное манипулирование большими объемами данных

— Data Mining (моделирование, интеллектуальный анализ данных) — поиск скрытых закономерностей, выявление причинно-следственных связей, анализ рисков

— KDD — Knowledge Discovery in Databases (обнаружение, извлечение знаний) — построение сценариев обработки от очистки и предобработки данных до моделирования.

В настоящем пособии рассматриваются только некоторые технологии из приведенного списка.

Последовательность действий (импорт, экспорт, обработка, визуализация) при решении конкретных задач в Deductor задается сценарием обработки. Сами же сценарии формируются специальным приложением Deductor Studio, которое является рабочим местом аналитика.

В профессиональной версии системы для импорта и анализа пригодны разнообразные табличные данные из стороннего источника (Oracle, MS SQL, Sybase, MS Access, Excel, 1С и др.). В учебной версии Deductor Academic — импортируются только данные в формате текстовых файлов с разделителями в виде табуляции.

Под обработкой данных в системе подразумевается любые действия, связанные с их преобразованием, такие как очистка данных, их трансформация и построение разнообразных моделей Data Mining.

При визуализации производится отображение полученных и обработанных данных. Аналитическая платформа самостоятельно анализирует формат отображения, предоставляя пользователю возможность выбора необходимого варианта.

В профессиональной версии системы предусмотрен экспорт (вывод) результатов обработки в виде файлов для последующего использования. В учебной версии Deductor Academic данная опция отсутствует.

В платформе Deductor представлено большинство основных технологий анализа, позволяющих достаточно быстро проектировать законченные аналитические решения, охватывающие весь цикл обработки данных. Это — многомерный анализ, нейронные сети, деревья решений, самоорганизующиеся карты, спектральный анализ и ряд других.

Применение подобных самообучающиеся методов и машинного обучения дает возможность создавать адаптивные информационные системы. Во многом такой подход делает более мягкими требования к квалификации персонала, приближая современные информационные технологии к более широкому кругу пользователей.

С помощью аналитической платформой Deductor появляется возможность извлекать из ранее накопленных и хранящихся в организации (в компании, в фирме, в департаменте государственного учреждения и др.) данные, интересную и практически полезную информацию, и тем самым трансформировать ее в знания, дающие существенные конкурентные преимущества.

Тиражирование же знаний обеспечивается за счет того, что все отчеты, модели, правила, полученные экспертом с помощью аналитической платформы Deductor, могут использоваться другими сотрудниками организации без необходимости понимания способов и методов получения этих результатов.

ЛИТЕРАТУРА К РАЗДЕЛУ I

— Deductor Integration Server — Руководство по установке и настройке Deductor Компания BaseGroup™ Labs

— Руководство администратора Deductor 5.3 Компания BaseGroup™ Labs

— Практикум Базовые навыки работы в Deductor Studio BaseGroup™ Labs, 2009

— Н. Ю. Прокопенко ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ АНАЛИЗА ДАННЫХ (аналитические информационные системы поддержки принятия решений на базе Deductor Studio Academic 5.2) Учебное пособие. Нижний Новгород2012.

II. Нейронные сети и их использование

Целью данной практической работы является ознакомление с примерами использования нейронных сетей для решения практических задач. Для выполнения работы используется свободно распространяемая аналитическая программная платформа «Deductor Academic» и программа работы с электронными таблицами MS Excel.

Нейронный сети — это большой класс информационных систем, построение которых имеет некоторую аналогию с структурой нервной ткани человеческого мозга. Нейросетевые технологии функционируют аналогично неосознанным мыслительным действиям человека. Нейронные сети в искусственном интеллекте — это упрощенные модели биологических нейронных сетей.

Известно, что нервная система и мозг человека состоят из нейронов, соединенных между собой нервными волокнами. Нервные волокна способны передавать электрические импульсы между нейронами. Нейрон является особой биологической клеткой, которая обрабатывает информацию. Элементарным преобразователем в искусственных нейронных сетях является искусственный нейрон, названный так по аналогии с биологическим прототипом.

Принципиальное отличие искусственных нейросетей от обычных программных систем состоит в том, что первые не требуют программирования и их можно обучить тому, что требуется пользователю.

Одна из наиболее распространенных архитектур нейронных сетей персептрон. Он построен по принципу иерархической сети, где каждый нейрон более высокого уровня соединен своими входами с выходами нейронов предыдущего слоя.

Для нейросетевой модели обработки данных характерно следующее:

— однородность системы (элементы нейронной сети одинаковы и просты, все определяется структурой связи)

— надёжность системы, построенной из ненадёжных элементов, за счёт избыточного числа связей

— «голографичность», предопределяющая, что при разрушении части система сохраняет свои свойства.

Структура искусственного нейрона и нейронной сети

Схема искусственного нейрона представлена на рис. А. Сумматор ∑ выполняет сложение сигналов Хi, поступающих по синаптическим связям от других нейронов, а также внешних входных сигналов. Синапсы осуществляют связь между нейронами, умножают входной сигнал Хi на число Wi, характеризующее силу связи между нейронами.

Нелинейный преобразователь f реализует нелинейную функцию преобразования значение выхода сумматора, согласно функции активации (передаточной функции) нейрона. Структура искусственного нейрона представлена ниже

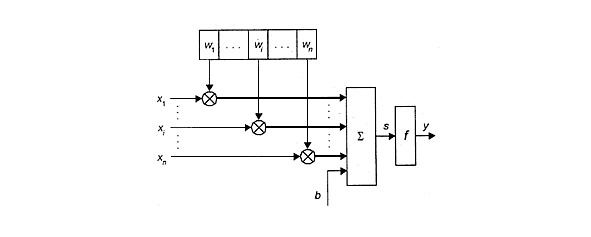
Данный вычислительный элемент — это весьма упрощенной математической моделью биологических нейронов. Поэтому подобные структуры иногда называют нейроноподобными элементами или формальными нейронами.

Примеры функций активации (нелинейных преобразователей) используемых в аналитической платформе Decuctor приведены ниже. Здесь a — параметр наклона функции активации, e — основание натуральных логарифмов

— — логистическая функция (она же сигмоид) f (х) = 1 / (1+e-aх)

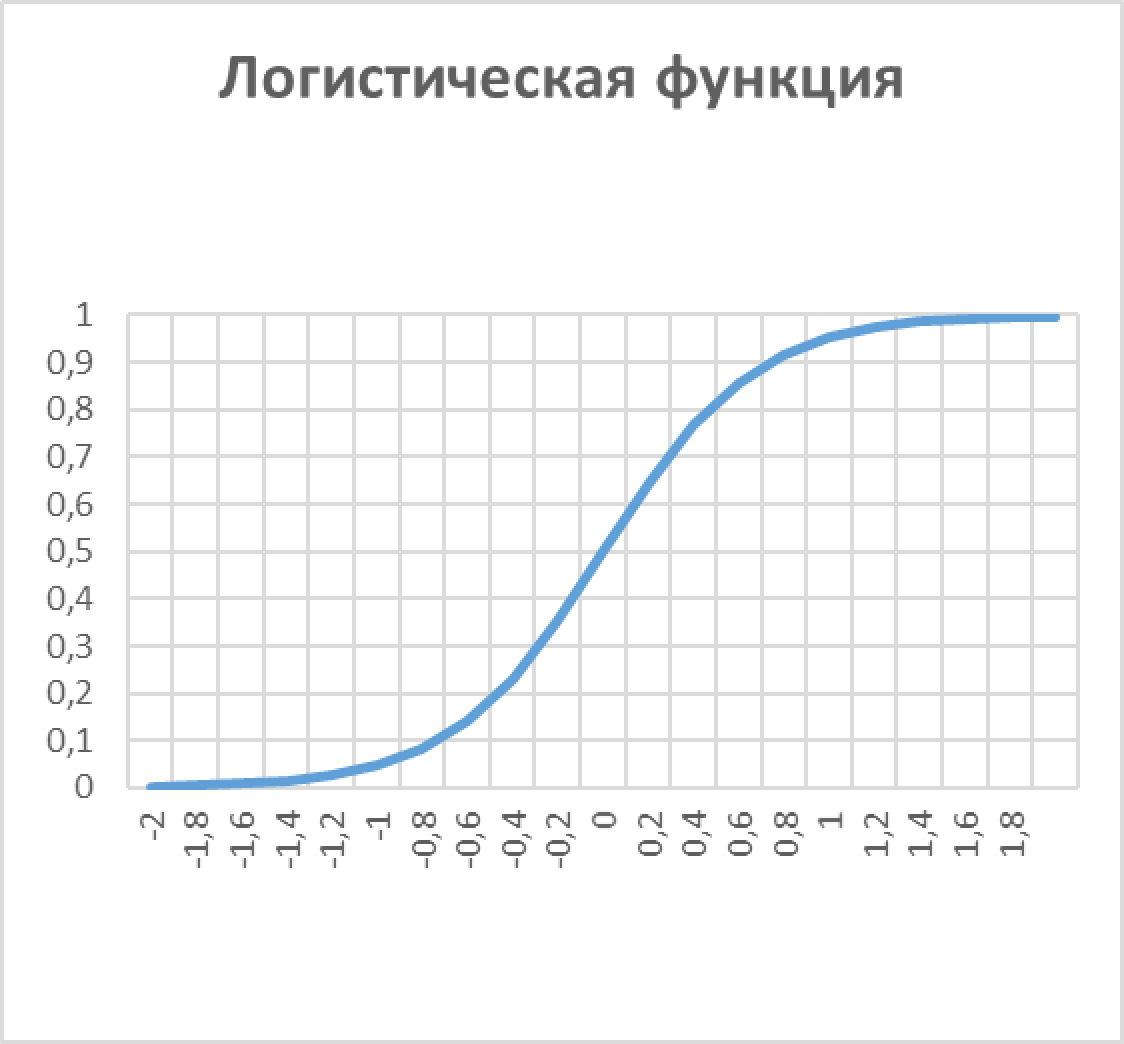
— — гиперболический тангенс th (x)

f (x) = (eax — e-ax) / (eax + e-ax)

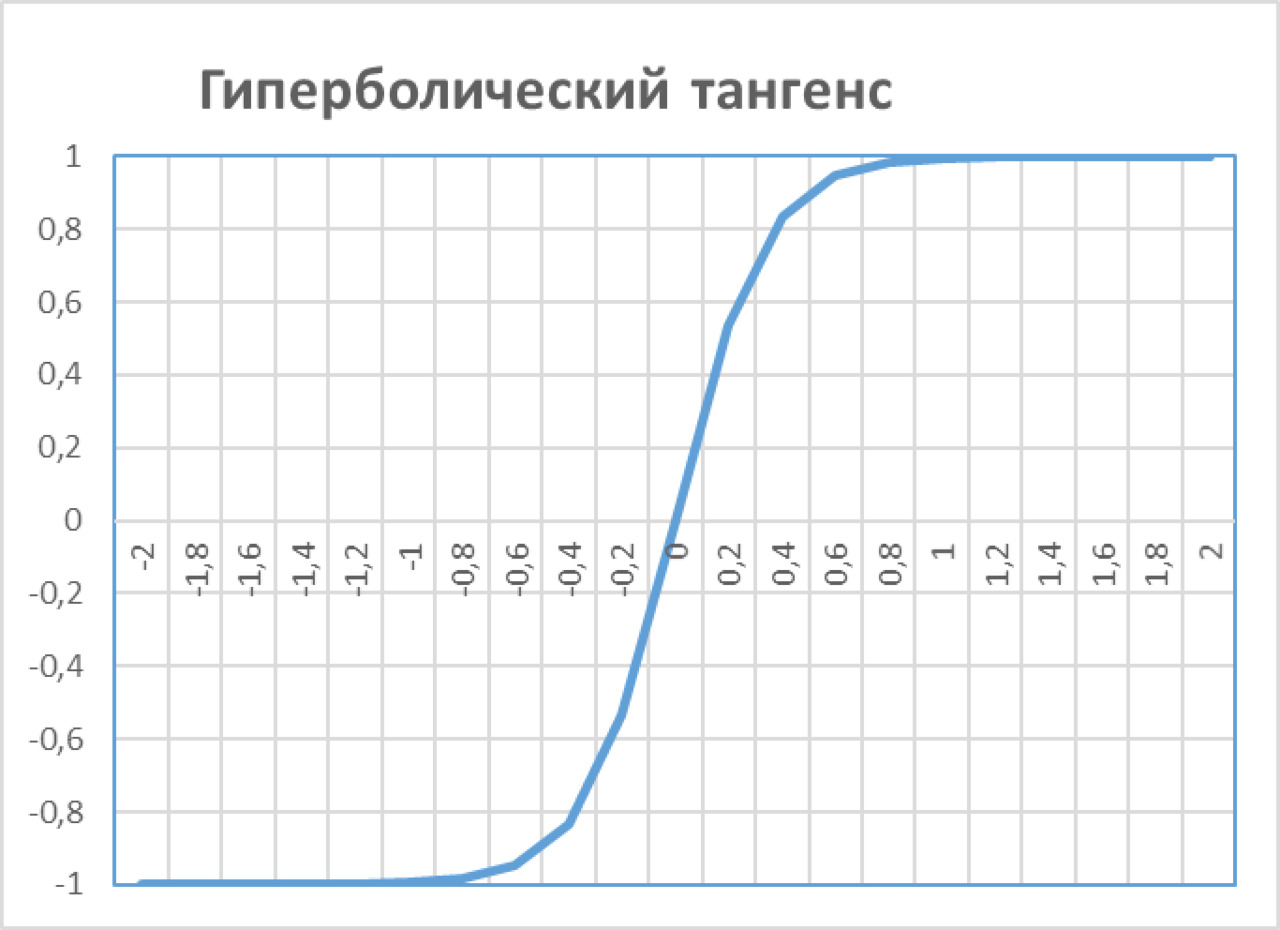
— — арктангенс f (x) = arctg (x)

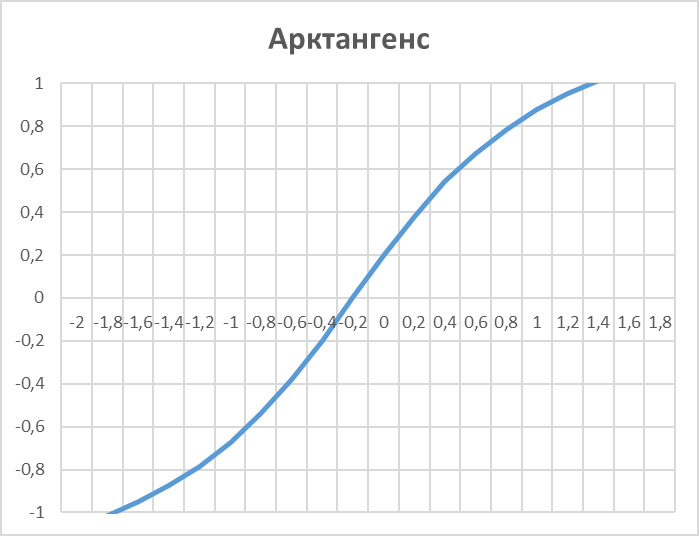
В основу концепции нейронных сетей положена идея коннекционизма. Согласно ней, нейроны можно моделировать довольно простыми автоматами и свойства нейронной сети определяются связями между нейронами. Каждая связь представляется как простой элемент, служащий для передачи сигнала.

Пример трехслойной нейронной сети, состоящей из десяти нейронов представлен на рисунке ниже

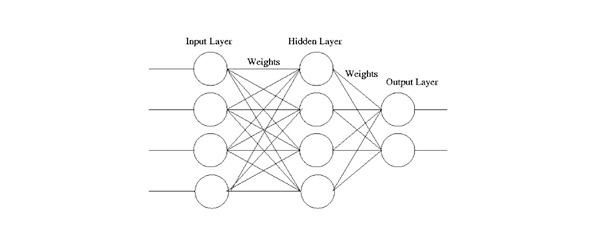
Известна также так называемая теорема о полноте, которая гласит, что любая непрерывная функция на замкнутом ограниченном множестве может быть равномерно приближена функциями, вычисляемыми нейронными сетями, если функция активации нейрона непрерывна и дважды непрерывно дифференцируема. Следовательно, нейронные сети являются универсальными структурами, позволяющими реализовать любой вычислительный алгоритм.

При решении конкретных задач на нейроны самого первого слоя подаются значения входных параметров, на основе которых нужно принимать какие-то решения, прогнозировать развитие ситуации и т. д.

Эти значения рассматриваются как сигналы, передающиеся в следующий слой, ослабляясь или усиливаясь в зависимости от числовых значений (весов), приписываемых межнейронным связям.

В результате на выходе нейрона самого верхнего слоя вырабатывается некоторое значение, которое рассматривается как ответ — реакция всей сети на введенные значения входных параметров.

Для того, чтобы нейронная сеть успешно функционировала, ее необходимо обучить, то есть «натренировать» на полученных ранее данных, для которых известны и значения входных параметров, и правильные ответы на них. Различают обучение нейронных сетей с «учителем» и «без учителя».

Тренировка состоит в подборе весов Wi межнейронных связей, обеспечивающих наибольшую близость ответов сети к известным правильным ответам. Для подбора значений весов межнейронных связей разработаны специальные методы. Например, метод обратного распространения ошибки, являющийся штатной опцией аналитической платформы Deductor.

Технология настройки нейронной сети является последовательной, итерационной процедурой. При конструировании нейронной сети один из наиболее сложных вопросов — определение количества слоев нейронов, количество нейронов в слое и структуру связей между нейронами) адекватное решаемой задаче. В настоящее время эффективные методы для точного решения задач выбора класса, архитектуры и строгая теория построения нейронных сетей, к сожалению, отсутствуют. Однако, это обстоятельство не слишком препятствует исследованию возможности их широкого применения

.

Литература к разделу II

— Ясницкий Л. Н. Интеллектуальные системы: учебник. М: Лаборатория знаний, 2016. — 221 с.

— Тадеусевич Р., Боровик Б., Гончаж Т., Леппер Б. Элементарное введение в теорию нейронных сетей с примерами программ / Перевод с польск. И.Д.Рудинского. М: Горячая линия — Телеком, 2011. — 408 с.

— Хайкин С., Нейронные сети. Полный курс. М: Издательство Вильямс, 2006. — 1101 с.

Задание №1
Проектирование нейронной сети для выполнения арифметических операций

Постановка задачи

Спроектировать нейронную сеть для выполнения арифметических операций сложения и умножения двух переменных А и В. Диапазон изменения входных переменных от 0 до 10. В результате выполнения задания должна быть спроектирована нейронная сеть с тремя входами (А, В, вход задания типа выполняемых действий «Операция») и одним выходом R (результат операции), представляющая собой трехслойный персептрон.

0. Формирование исходных данных для построения нейронной сети, реализующей арифметические операции

Модели, реализованные на основе нейронных сетей, обучаемы. В данной работе мы рассмотрим алгоритм «обучение с учителем». При его использовании нейронной сети предъявляются значения как входных, так и желательных выходных сигналов, и она, по некоторому внутреннему алгоритму, подстраивает веса своих синоптических связей. Для реализации процесса обучения необходимо сформировать файл Обучающие данные. txt

Для этого:

0.1 Запустите программу Excel

0.2 Создайте с помощью программы Excel таблицу, состоящую из 5 столбцов и 200 строк.

0.3 Сохраните полученный файл в формате «Текстовые файлы (с разделителями табуляции)» под именем Обучающие данные. txt.

Ввод исходных данных

Исходным числовым массивом для решения этой задачи служит созданный ранее файл Обучающие данные. txt с результатами сложения и умножения. В этом файле в столбцах «А» и «В» представлены операнды, в столбце «Операция» — вид операции (сложение/умножение), а в столбце «R» — результаты выполнения арифметического действия.

1.1. Запустите программу Deductor Studio Academic и создайте новый проект

1.2 Инициируйте «Мастер импорта»

1.3 Укажите импорт данных из текстового файла

1.4 Выберите в качестве загружаемого файл Обучающие данные. txt.

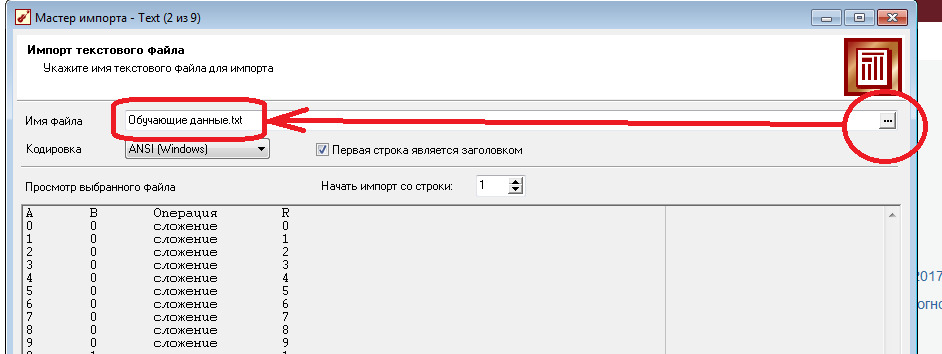
1.5 Импортируйте выбранный файл

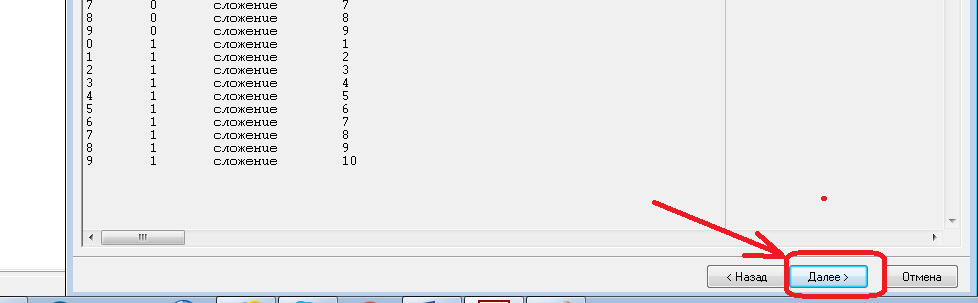
1.6 Установите форматы импорта и разделители по умолчанию.

1.7 Установите тип данных для операндов А, В и результата R — вещественный.

1.8 Запустите кнопкой «Пуск» процесс импорта данных в аналитическую систему.

1.9 Определите отображение данных в виде таблицы и завершите импорт, нажав кнопку «Готово». В результате проделанных действий обучающий массив будет введен в буфер аналитической системы Deductor.

Построение нейронной сети при помощи мастера обработки

Решение данной задачи произведите с помощью эмулятора нейронных сетей — штатной опцией аналитической системы Deductor. Мастер обработки системы позволяет сконструировать нейронную сеть с заданной структурой, определить ее параметры и обучить ее с помощью одного из доступных в системе алгоритмов обучения.

Для этого

2.1. Находясь на узле импорта, откройте мастер обработки

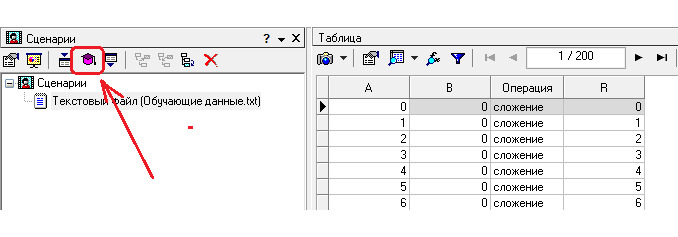
2.2 Выберите режим обработки «Нейросеть»

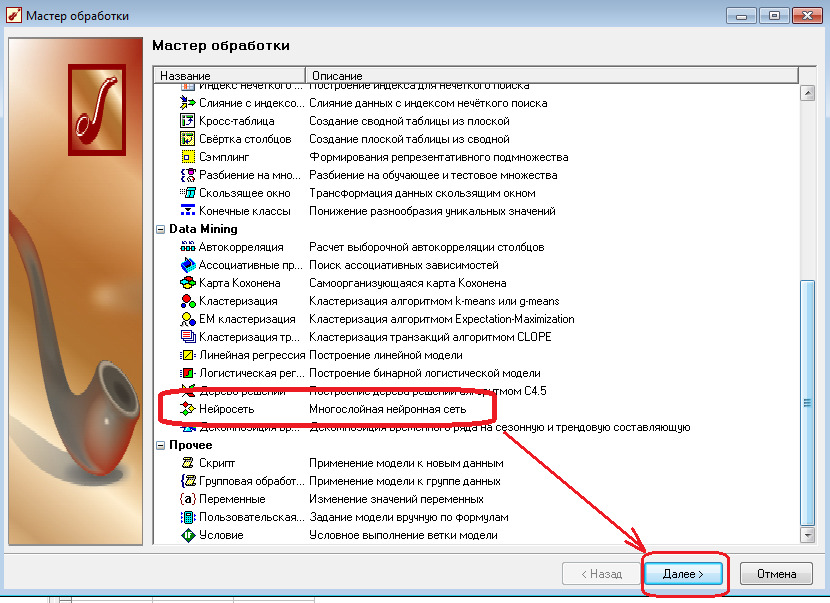
2.3 Установите назначение полей «А», «В» «Операция» как входные, а поле «R» — как выходное.

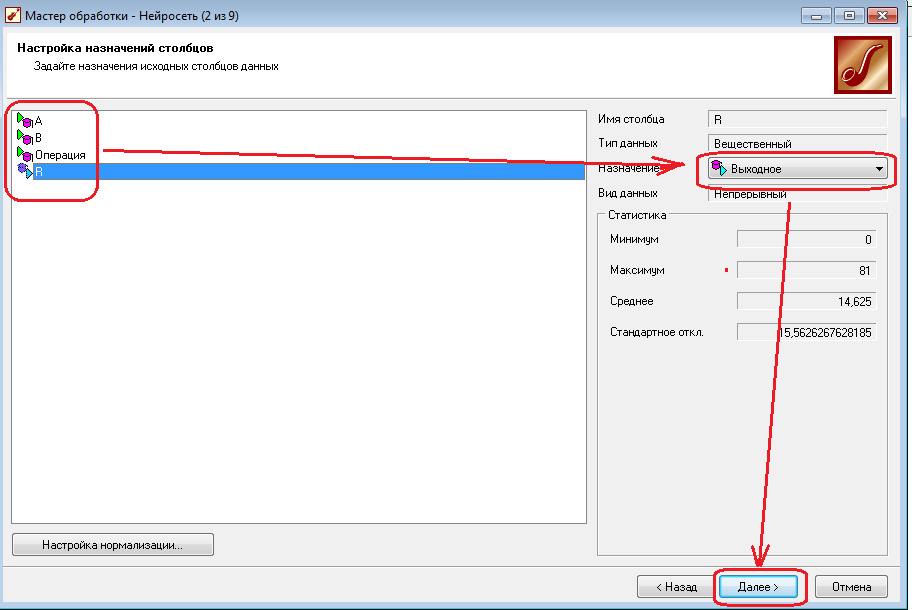
2.4 Разделите исходное множество данных на обучающее и тестовое, используя параметры «по умолчанию». То есть, установите размер обучающего множества 95%, а тестового 5%. Укажите способ разбиения исходного множества данных «Случайно».

Это означает, что из всего набора данных пять процентов случайным образом выбранных значений используется для контроля работоспособности построенной нейронной сети, остальные 95% данных используются для обучения нейросети подбором синоптических весов межнейронных связей Wi. с помощью специальных алгоритмов.

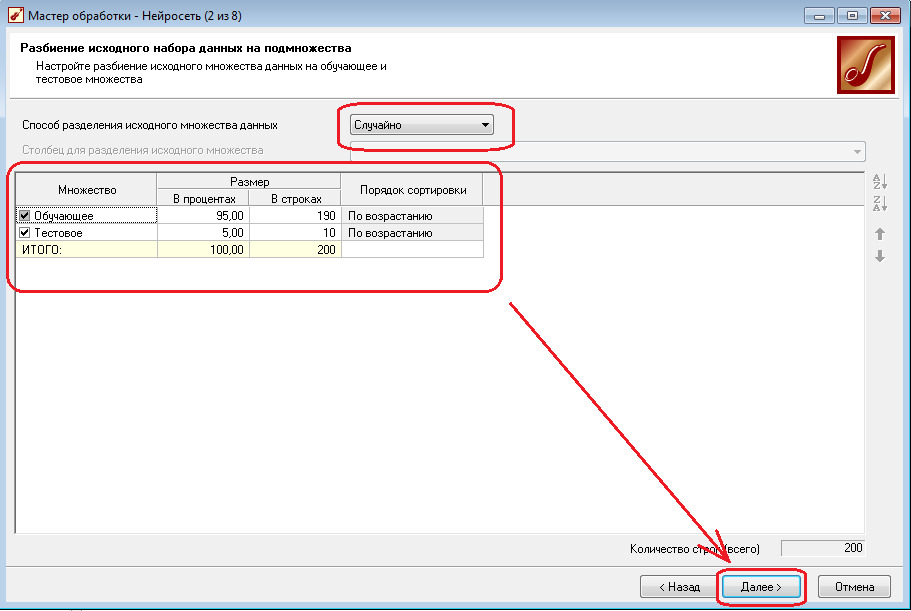
2.5 Существуют различные полуэмпирические формулы для определения количества нейронов в нейронной сети достаточного для решения поставленной задачи. Установите это количество равным двадцати четырем. Остальные параметры при построении нейронной сети оставьте по умолчанию.

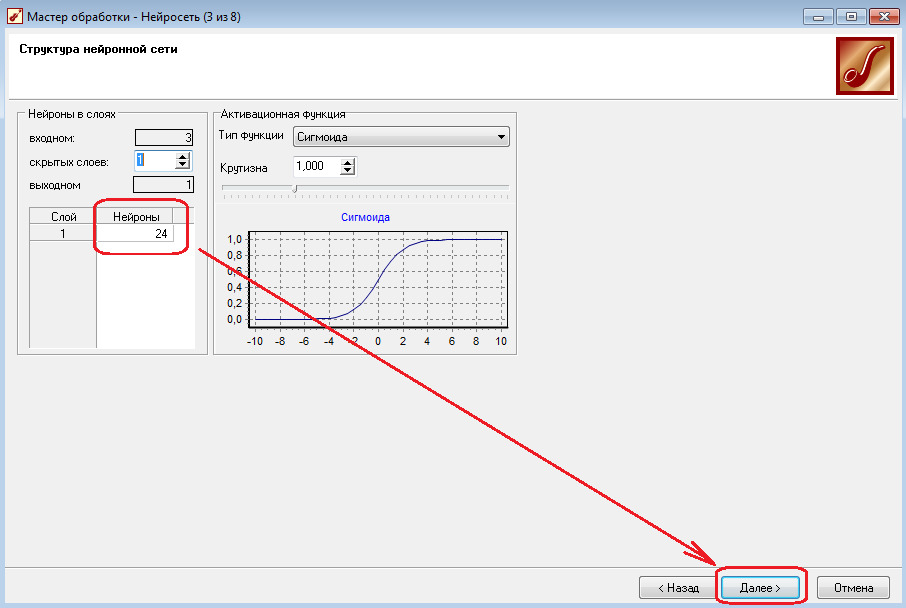
2.6 Оставьте исходным алгоритм обучения и его параметры (Нажав «Далее»).

2.7 Установите параметры остановки обучения нейронной сети — ошибку менее 0,01 или достижение эпохи обучения 25000.

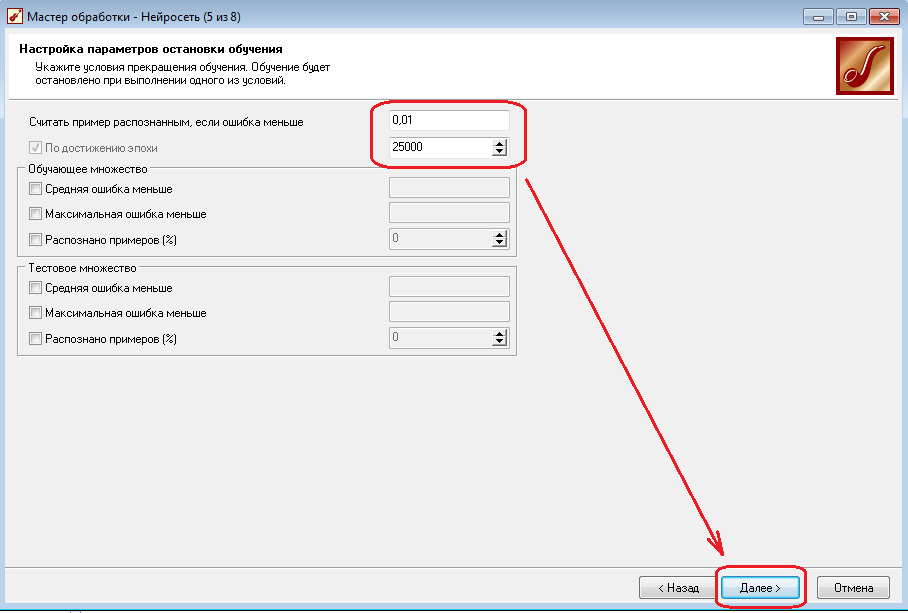
2.8 Запустите процесс обучения нейронной сети, нажав кнопку «Пуск».

Наблюдайте изменение величины ошибки, а также процента распознанных примеров.

Во время процесса обучения нейросети происходит автоматический подбор весовых коэффициентов связи между ее отдельными нейронами, согласно штатному алгоритму, реализованному в аналитической платформе Deductor (в системе используется алгоритм обратного распространения ошибки).

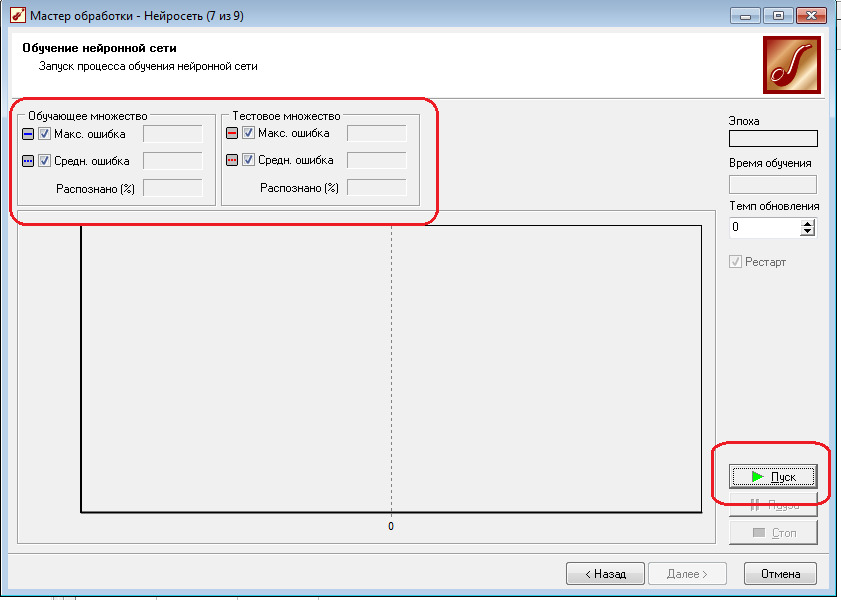
Как правило, обучение занимает несколько минут. При необходимости пользуйтесь кнопками «Стоп» и «Пауза».

После остановки обучения нажмите «Далее».

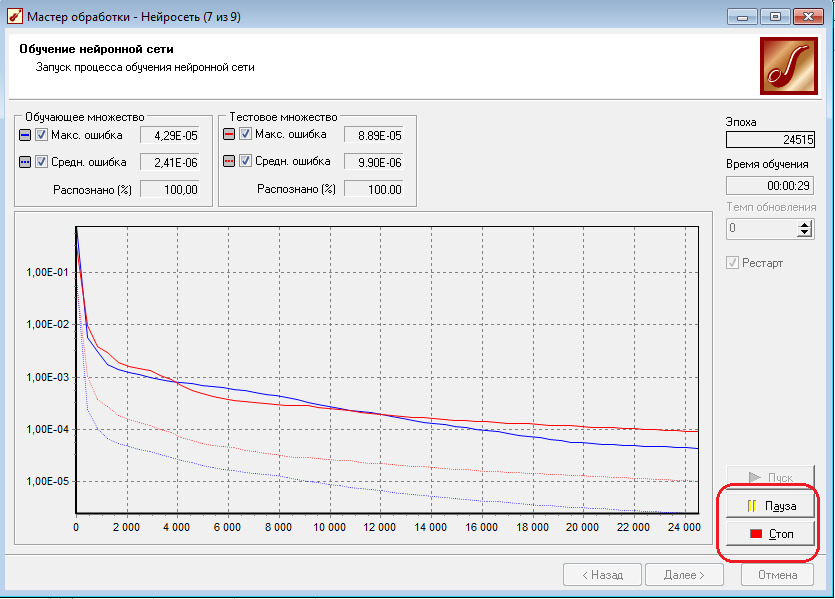
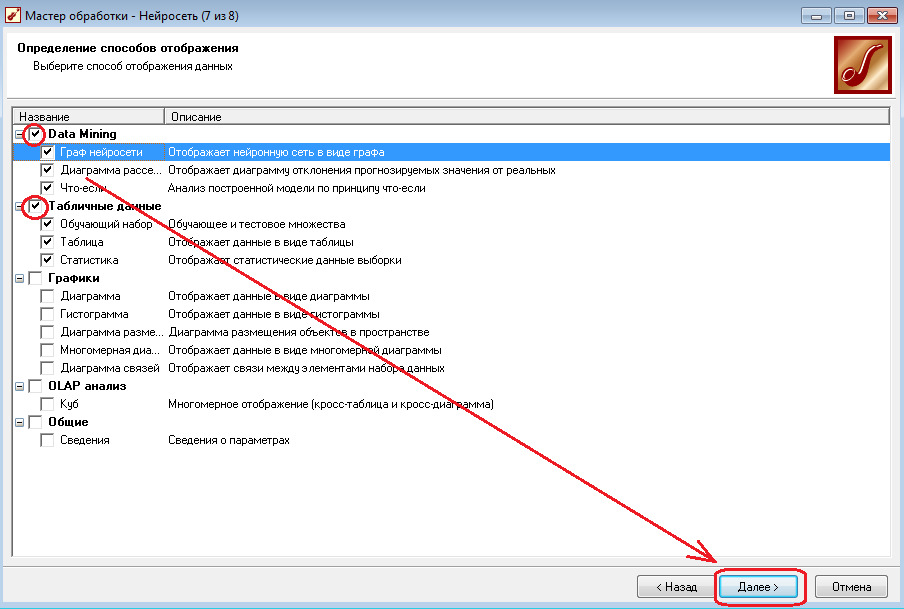
2.9 После окончания обучения выберите визуализаторы Data Minig («Граф нейросети», «Диаграмма рассеяния», «Что-если») и Табличные данные («Обучающий набор», «Таблица» и «Статистика»).

В результате обучения нейросети будут получены

A. Граф нейросети

Структура полученной нейронной сети представлена на ее графе. На нем приведена схема связей между отдельными нейронами. Нейроны (они представлены на рисунке красными точками) взаимодействуют при помощи синаптических связей (представлены в виде линий) с весовыми коэффициентами передачи сигнала, найденными в процессе обучения.

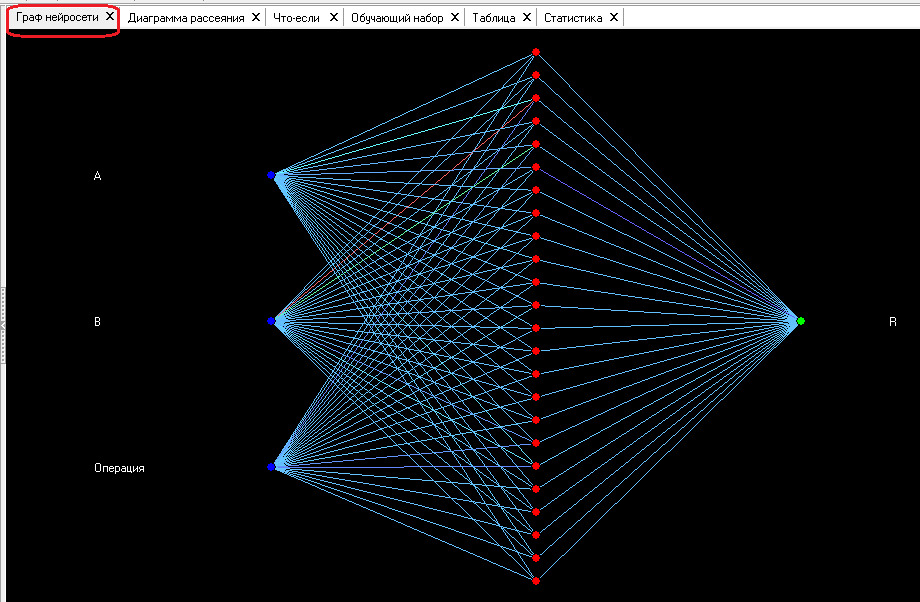
Цвет найденной связи соответствует ее величине. Красный — сильная связь, синий — слабая.

Диаграмма рассеяния показывает расхождение прогнозируемых данных относительно эталонных.

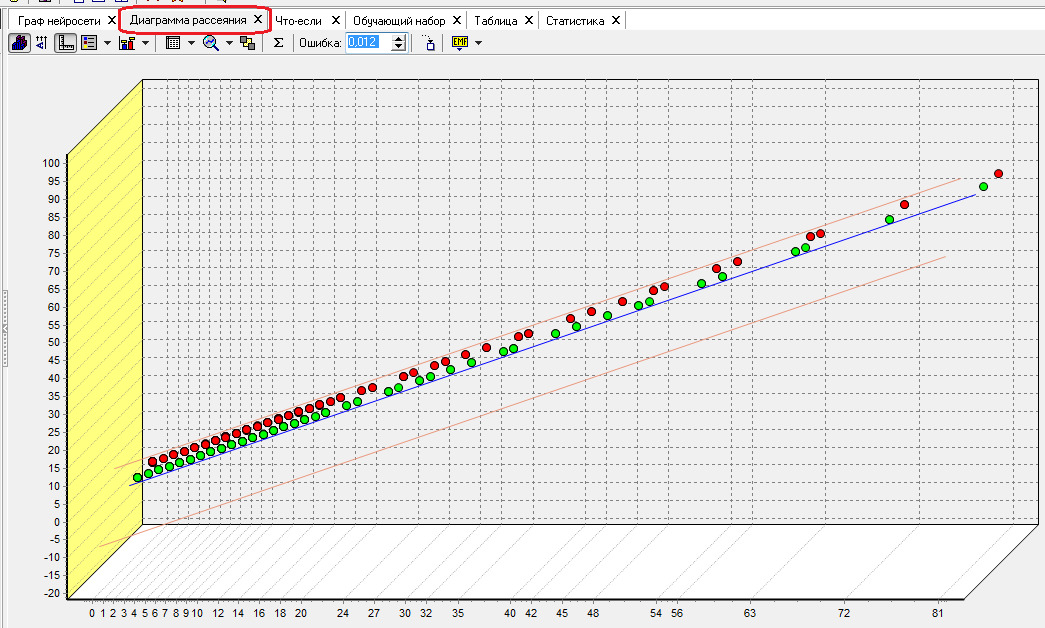
На рисунке показано графическое представление эталонных значений и результатов, полученных при использовании нейронной сети.

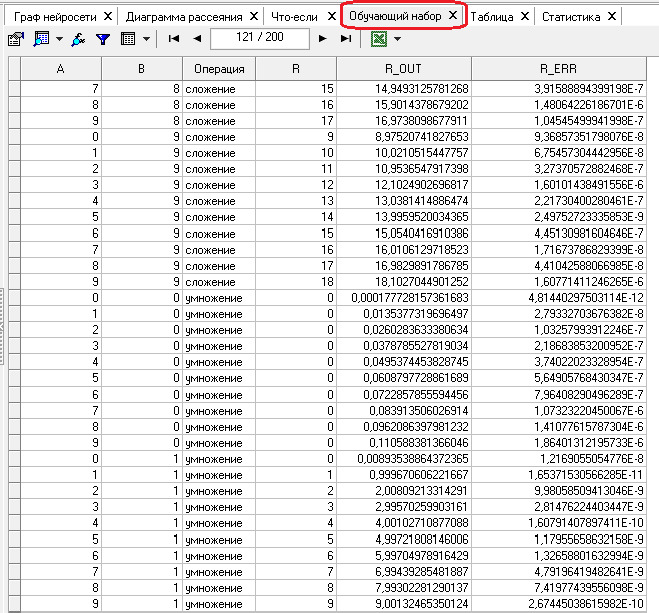
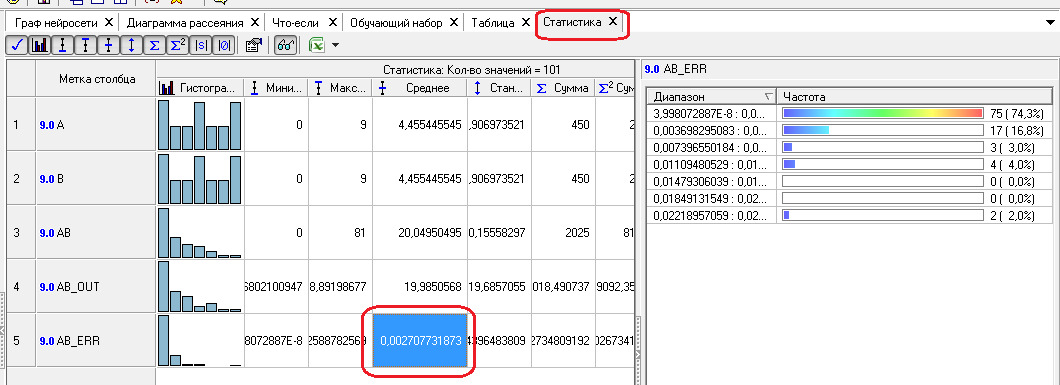
B. Таблица результатов, где А и В исходные операнды, R — эталонное значение результата, АВ_OUT — результат полученный от нейронной сети, а АВ_ЕRR — значение абсолютной ошибки.

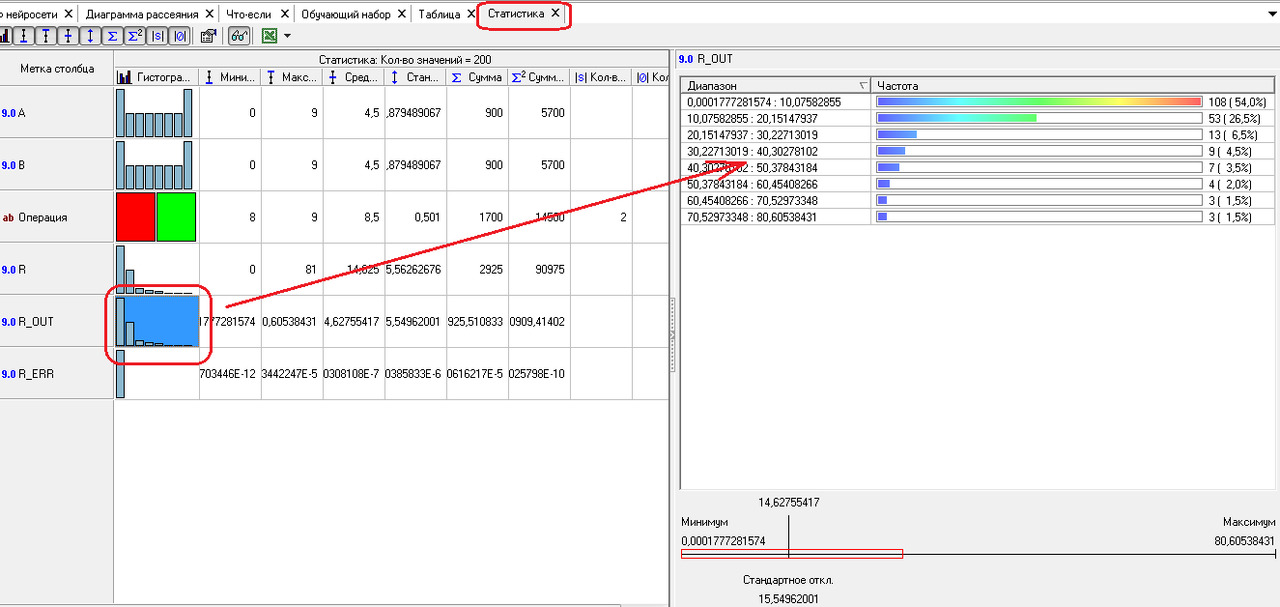
C. Cтатистические характеристики: в данном примере наибольший интерес представляют характеристики ошибки моделирования.

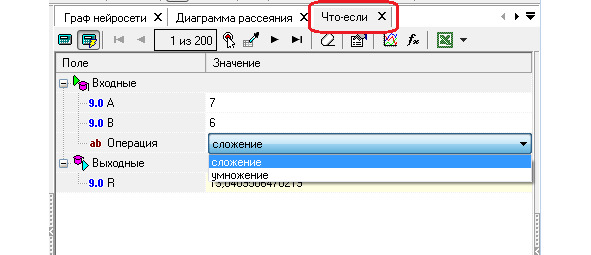
D. Инструмент для проведения вычислений «Что-если», так как введя значения операндов А и В можно рассчитать их сумму или их произведение.

2.10 Сохраните полученный сценарий в файле (имя файла произвольно) нажав Файл — > Сохранить как — > Сохранить

Задание №2
Проверка правильности выполнения нейронной сетью операций умножения и сложения

Постановка задачи

В результате выполнения задания должны быть получены характеристики, отражающие точность выполнения операций нейронной сетью.

2.11. В зависимости от вашего номера в журнале группы выберите данные для проверки. Произведите проверку выполнения операций сложения и умножения для десяти различных комбинаций операндов А и В, приведенных в Таблице №1.

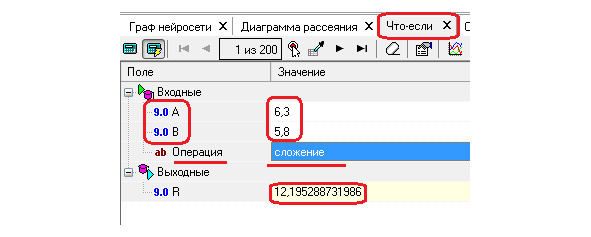
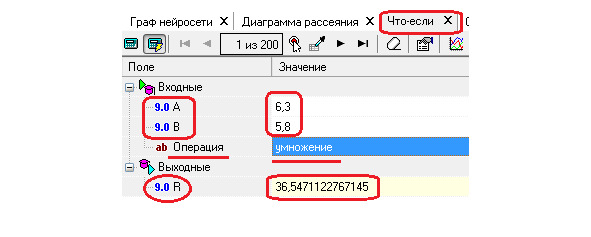
Таблица №1

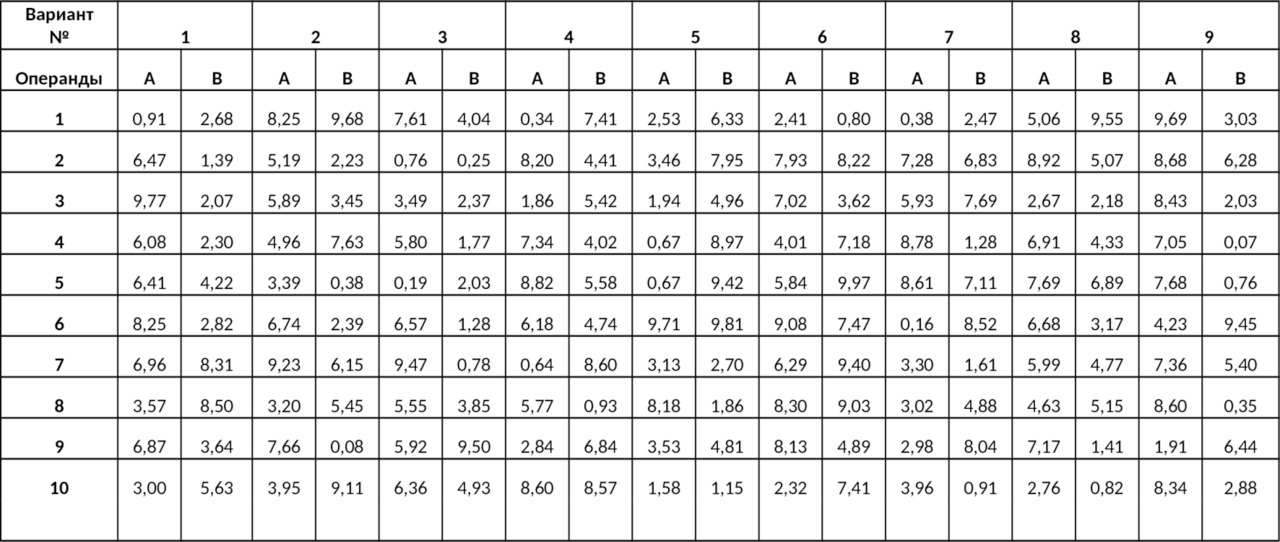
Таблица №1 (продолжение)

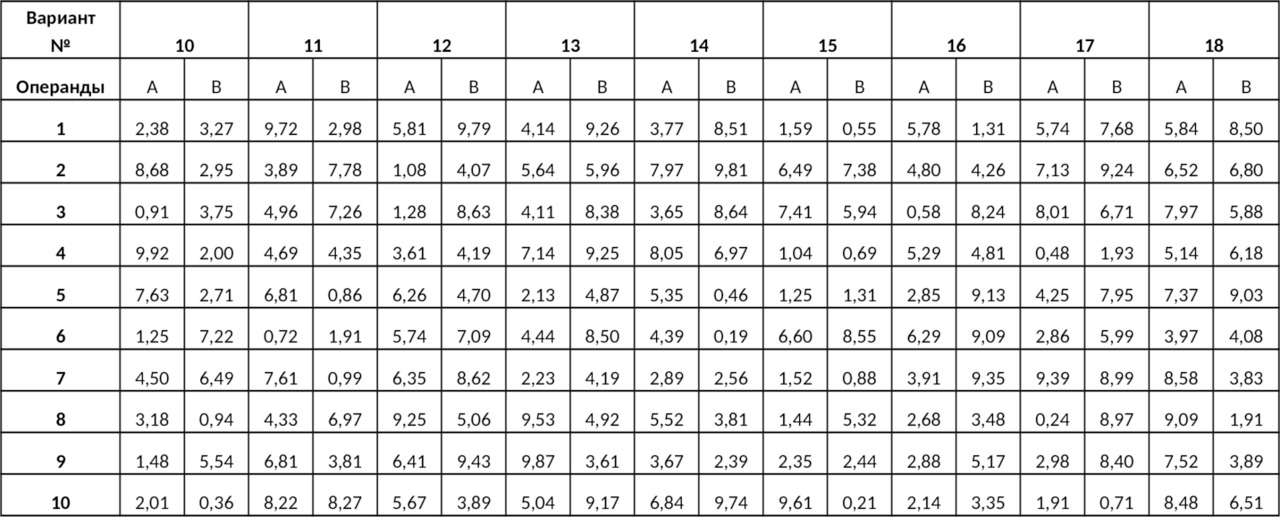
Полученные результаты (с тремя знаками после запятой) занесите в Таблицу №2. Указание: для проведения расчетов используйте программу Excel.

Таблица №2

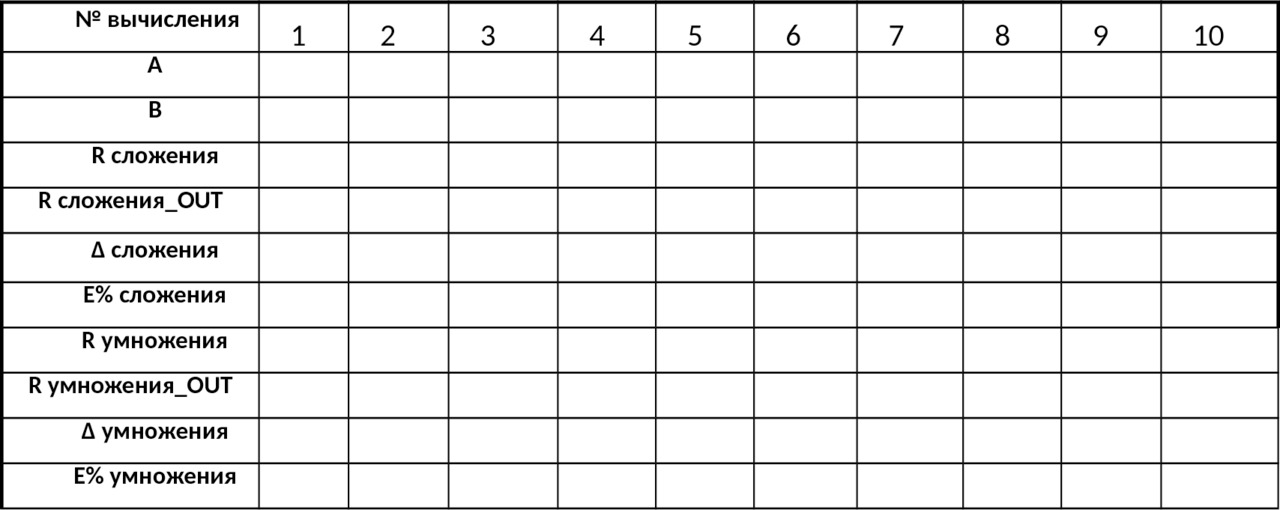
В Таблице №2 представлены

А и В — операнды

R сложения — результат сложения операндов, полученный с помощью программы Excel

R сложения _OUT — результат сложения, полученный с помощью нейронной сети

Δ сложения =ABS (R сложения — R сложения _OUT) — абсолютная ошибка нейронной сети при выполнении операции сложения.

Е = (Δ сложения / R сложения) *100% — относительная ошибка нейронной сети при выполнении операции сложения.

R умножения — результат умножения операндов, полученный с помощью программы Excel

R умножения _OUT — результат умножения, полученный с помощью нейронной сети

Δ умножения =ABS (R умножения — R умножения _OUT) — абсолютная ошибка нейронной сети при выполнении операции умножения.

Е = (Δ умножения/R умножения) *100% — относительная ошибка нейронной сети при выполнении операции умножения.

2.12. Найдите величины

— наибольшей и наименьшей абсолютной ошибки вычислений при операциях сложения и умножения

— наибольшей и наименьшей относительной ошибки вычислений при операциях сложения и умножения

— средней абсолютной ошибки при операциях сложения и умножения

— средней относительной ошибки при операциях сложения и умножения

Полученные результаты отразите в отчете.

Задание №3. Исследование зависимости точности выполнения операций от количества нейронов

Постановка задачи:

Исследуйте зависимость точности моделирования выполняемых операций от количества нейронов.

Определение оптимального количества нейронов — важная задача при построении нейронной сети. Существует два основных подхода к решению этой задачи — конструктивный и деструктивный.

При первом вначале берется сеть минимального размера, и постепенно увеличивают ее размер до достижения требуемой точности. При этом на каждом шаге ее заново обучают.

При деструктивном подходе вначале берется сеть завышенного размера, и затем из нее удаляются узлы и связи, мало влияющие на решение. Существует следующее правило: число примеров в обучающем множестве должно быть больше числа настраиваемых весов (связей).

В результате выполнения задания должен быть получен график зависимости точности от количества нейронов в нейронной сети.

Практическая часть

3.1. Проделайте действия аналогичные указанным в пп. 2.1—2.3.

3.2. Установите активационную функцию в зависимости от вашего варианта согласно Таблице №4, аналогично пункту п. 2.4.

В Таблице №3 приведены конкретные значения параметров (тип функции активации: сигмоида, гипертангенс, арктангенс и значение ее крутизны для каждого из вариантов.

Таблица №4

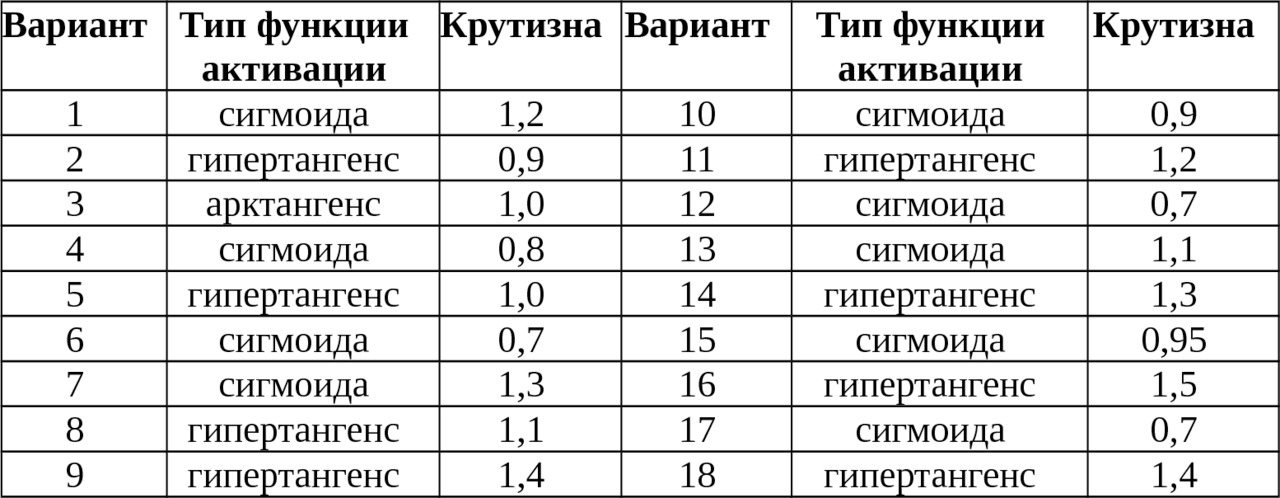
Различный вид функции активации и ее крутизна задается так, как показано на рисунке ниже

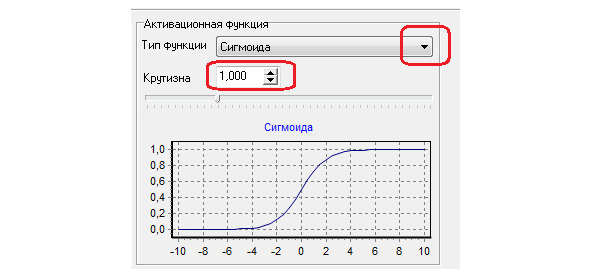
3.3. Последовательно изменяйте количество нейронов внутреннего слоя в диапазоне от 4 до 22 с шагом 2 и проводите построение нейронных сетей.

3.4. Устанавливайте соотношение между тестовой и обучающими выборками как 5% и 95%.

3.5. Устанавливайте ошибку распознавания менее 0,005, а количество эпох обучения не более 35000.

3.6. При построении каждой новой нейросети перемещайте курсор в позицию «Текстовый файл».

3.7. Задавайте визуализатору (аналогично выполнению пункта 2.8) значения «Диаграммы рассеяния» и «Статистика». Фиксируйте значения средней ошибки.

— Проделайте построение нейронной сети десять раз, изменяя условия согласно описанию, приведенному выше в параграфе 3.3.

— Получите график зависимости величины средней ошибки от количества нейронов в скрытом слое нейросети, подобный приведенному ниже (при помощи Excel).

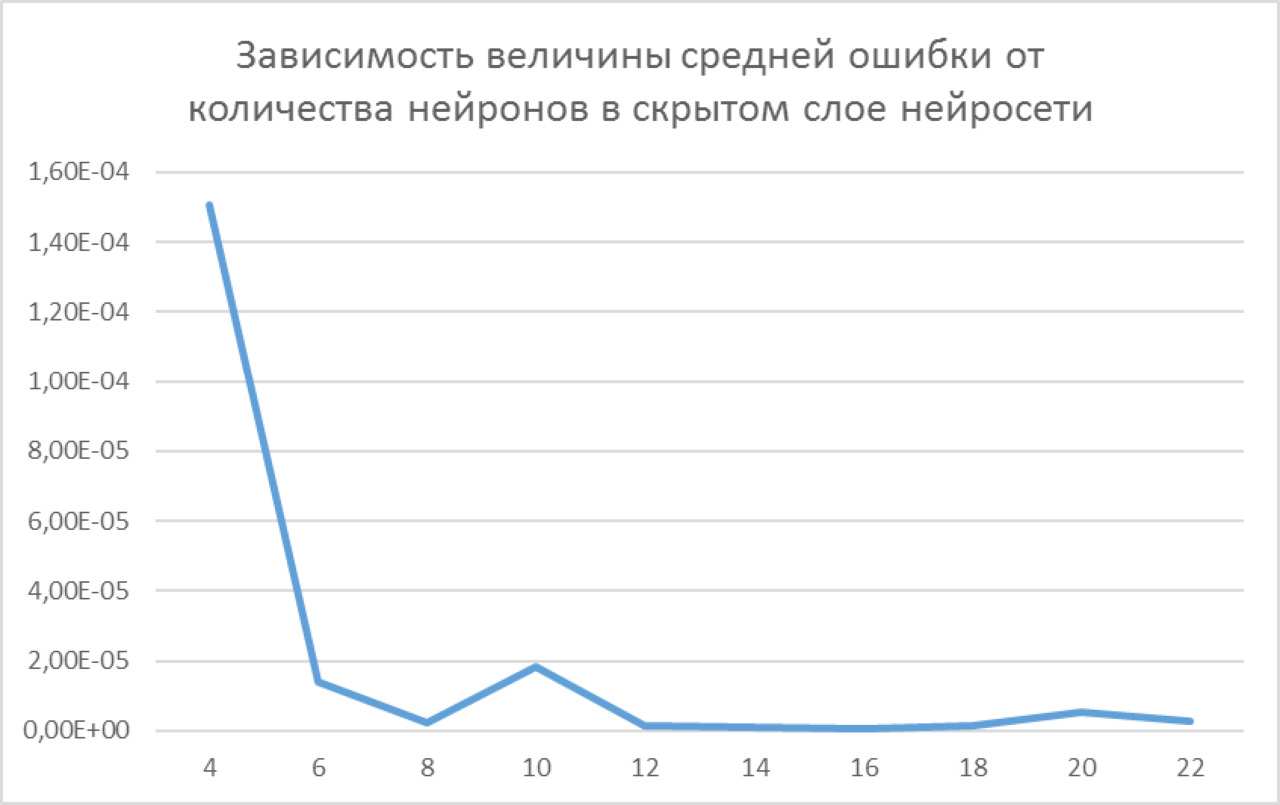
— Определите то количество нейронов, которое обеспечивает минимальную среднюю ошибку в данном диапазоне изменения числа нейронов.

Задание №4. Построение прототипа медицинской информационной диагностической системы, использующей технологию нейронных сетей

Постановка задачи

Создайте прототип диагностической информационной системы для определения диагноза заболевания по известным симптомам. Она должна представлять из себя нейронную сеть распознающую диагноз по набору симптомов. В качестве исходных данных используйте результаты, полученные в медицинской практике. и находящийся в файле ДИАГНОСТИКААППЕНДИЦИТА. txt. Этот файл представляет собой таблицу симптомов, соответствующих определенному диагнозу.

4.1. Загрузите в аналитическую систему Deductor исходные данные из файла ДИАГНОСТИКА АППЕНДИЦИТА. txt, проделав действия аналогичные пп.1.1—1.9.

4.2. Постройте нейронную сеть с 16 нейронами, проделав действия аналогичные пп.2.1—2.10, задавая функцию активации и ее крутизну в зависимости от вашего варианта согласно таблице №4.

4.3. Зафиксируйте в отчете результирующую Таблицу сопряженности

4.4. Проделайте действия, аналогичные пп.4.1—4.3 для файла ДИАГНОСТИКА ПОЧКИ. txt.

Требование к оформлению отчета о практической работе

Отчет о данной части практической работы должен содержать:

a) Титульный лист, оформленный согласно установленным требованиям

b) Граф нейросети, предназначенной для выполнения операций «умножение» и «сложение» (п.2.8)

c) Таблицу результатов, полученных в п.2.10 инструкции (исходные операнды, эталонное значение результата, результат полученный от нейронной сети и величина ошибки)

d) Значения величин, найденных в п.2.11 инструкции (наибольшую и наименьшую абсолютную ошибку вычислений, наибольшую и наименьшую относительную ошибку вычислений, среднюю абсолютную ошибку, среднюю относительную ошибку).

e) График зависимости, полученной в п.3.9 инструкции

f) Количество нейронов, обеспечивающий минимальную среднюю ошибку при решении задачи (п.3.10 инструкции)

g) Таблицы сопряженности, полученные в п.4 настоящей инструкции.

Контрольные вопросы

1. Что такое нейронные сети

2. В чем заключается принципиальное отличие нейронных сетей от обычных программных систем

3. Что такое персептрон

4. Что характерно для нейросетевой модели обработки данных

5. Из каких элементов состоит искусственный нейрон

6. Приведите примеры наиболее распространенных функций активации

7. Что необходимо для успешного функционирования нейронной сети

8. Как производится «тренировка» нейронной сети

9. Перечислите основные недостатки нейронных сетей

10. Что такое эмулятор нейронных сетей

11. Что такое таблица сопряженности в аналитической платформе Deductor.

III. Построение и обучение самоорганизующихся карт признаков (карт Кохонена)

В данном практической работе используем самоорганизующиеся карты Кохонена для кластеризации продуктов питания в зависимости от содержащихся в них компонентов и кластеризацию студентов Факультета государственного в зависимости от их рейтингов.

В ходе работы проводится формирование структуры самоорганизующейся карты, параметров обучения, оценка эффективности кластеризации и содержательная интерпретация кластеров.

Кластеризация — группировка объектов, характеристики которых можно описать векторами признаков в многомерном пространстве, в группы, называемые кластерами. В результате кластеризации объекты близкими значениями признаков группируются в один кластер. Кластеризацию обычно используют при отсутствии изначальных сведений о классах исследуемых объектов, а также в тех случаях, когда число объектов велико.

Основные проблемы возникающие при решении задачи кластеризации проистекают от того, что оптимальное количество кластеров в общем случае неизвестно, а выбор меры «похожести» или близости свойств объектов между собой, как и критерия качества кластеризации, часто носит весьма субъективный характер.

Поэтому, обычно считается, что кластер — это массив векторов (объектов), расстояние между которыми (между характеристиками объектов) внутри кластера всегда меньше, чем до любого вектора другого кластера. То есть кластер — область векторного пространства, содержащая группу близко расположенных векторов.

Кластерный анализ данных состоит из следующих шагов:

1. Построение кластеризационной модели на обучающем множестве.

2. Содержательная интерпретация кластеров — изучение свойств объектов, попавших в каждый кластер.

3. Оценка состоятельности модели.

4. Практические использование модели: модели предъявляются новые наблюдения, которые она относит к одному из кластеров.

При некотором сходстве классификации и кластеризации (и в том, и в другом случае требуется объединять наблюдения в группы) существует весьма существенное отличие. Если случае классификации классы заранее заданы для каждого примера, то при кластеризации — нет.

Кластеризация преодолевает основной недостаток классификации — когда любой новый объект обязательно должен быть отнесен к одному из классов, даже если он ни к одному из них отношения не имеет. В случае кластеризации «нетипичные» объекты сформируют новый кластер, что позволит выделить их.

Нейронные сети, называемые картами Кохонена (Self-Organizing Maps, SOM), — это одна из разновидностей нейронных сетей. Их особенность — неконтролируемое обучение (то есть обучение без учителя). Методика заключается в подстройке весов связей между нейронами. При таком обучении нейронная сеть как бы «учится понимать» структуру данных, так как обучающее множество состоит лишь из значений входных переменных и в процессе обучения не происходит сравнивания выходов нейронов с эталонными значениями.

Такая подстройка весов может производиться только на основе информации о состоянии нейронов и уже имеющихся весовых коэффициентах, при этом отсутствует информация об ошибке и такой процесс часто называют самоорганизацией нейронной сети.

В основе идеи сети Кохонена лежит аналогия со свойствами человеческого мозга. Кора головного мозга. обладает определенными топологическими свойствами. То есть участки коры головного мозга, ответственные за близкие части тела, примыкают друг к другу и все изображение человеческого тела как бы отображается на его поверхность.

По своей структуре сеть Кохонена достаточно проста. Она имеет только два слоя нейронов: входной и выходной. Иногда ее также называют самоорганизующей картой. Изначально количество нейронов в выходном слое должно быть много больше чем количество возможных кластеров.

Сеть Кохонена обучается методом последовательных приближений. В процессе такого обучения на входы подаются данные, но сеть подстраивается не под эталонное значение выхода, а под имеющиеся закономерности во входных данных.

В начале обучения синаптические веса межнейронных связей инициализируются случайными значениями и обучение начинается с сформированного случайным образом выходного расположения возможных центров (кластеров).

При подаче обучающего примера на вход сети определяется тот нейрон второго слоя менее всего реагирующий подаваемый сигнал, то есть у которого скалярное произведение синоптических весов и поданного на вход исходного вектора набора данных минимально. Этот нейрон объявляется победителем в данную эпоху обучения нейронной сети.

Для нейрона нейрона-победителя находится группа ближайших к нему нейронов выходного слоя, определяемых параметром радиус обучения. Эти нейроны и будут являться центром при подстройке их синоптических весов, когда они должны последовательно приближаться к параметрам нейрона победителя с заданной скоростью. Радиус и скорость обучения как правило изменяются в процессе обучения и на начальном этапе они больше.

Через определенное число эпох обучения производится перемешивание порядка подачи обучающих данных. Такой алгоритм предполагает «соревновательное» обучение. Оно заключается не в минимизации ошибки, а в подстройке весов (внутренних параметров нейронной сети) для наибольшего совпадения с входными данными.

При своей реализации итерационный алгоритм Кохонена последовательно проходит ряд эпох, на каждой из которых обрабатывается один пример из обучающей выборки. После предъявления достаточного количества примеров нейронная сеть становится способной определить кластеры, то есть она организуются таким образом, что топологически близкие узлы (лежащие на карте Кохонена рядом) становятся чувствительными к похожим входным данным.

В результате работы алгоритма центры кластеров устанавливается в определенной позиции, удовлетворительным образом кластеризующей предъявленные примеры. В результате обучения сети также определяется мера соседства нейронов, т.е. окрестность нейрона-победителя.

Полученное графическое представление удобно использовать как средство визуализации при анализе данных, так как карта Кохонена классифицирует входные примеры на кластеры (группы схожих примеров) и визуально отображает многомерные входные данные на плоскости нейронов.

Уникальность метода самоорганизующихся карт состоит в преобразовании n-мерного пространства в двухмерное. Из наиболее распространенных применений карт Кохонена можно отметить: разведочный анализ данных и обнаружение новых явлений.

Разведочный анализ данных. Сеть Кохонена способна распознавать кластеры в данных, а также устанавливать близость классов. Таким образом, пользователь может улучшить свое понимание структуры данных. Если в данных распознаны классы, то их можно обозначить, после чего уже решать задачи классификации. Сети Кохонена можно использовать и в тех задачах классификации, где классы уже заданы, — тогда преимущество будет в том, что сеть сможет выявить сходство между различными классами.

Обнаружение новых явлений. Сеть Кохонена распознает кластеры в обучающих данных и относит все данные к тем или иным кластерам. Если встретится уникальный набор данных, не похожий ни на один из известных образцов, то тем самым выявится его новизна.

ЛИТЕРАТУРА К РАЗДЕЛУ III

— Ф. Уоссермен, «Нейрокомпьютерная техника», М.: Мир, 1992

— А. Ежов, С. Шумский, «Нейрокомпьютинг и его применение в экономике и бизнесе», 1998.

— Гвидо Дебок, Тойво Кохонен Анализ финансовых данных с помощью самоорганизующихся карт, М.: Издательство Альпина, 2001

— Deductor Руководство аналитика Версия 5.3 © 1995—2013 Компания BaseGroup™ Labs

Задание №1 Использование карт Кохонена для кластеризации продуктов питания с автоматическим определением количества кластеров

Постановка задачи

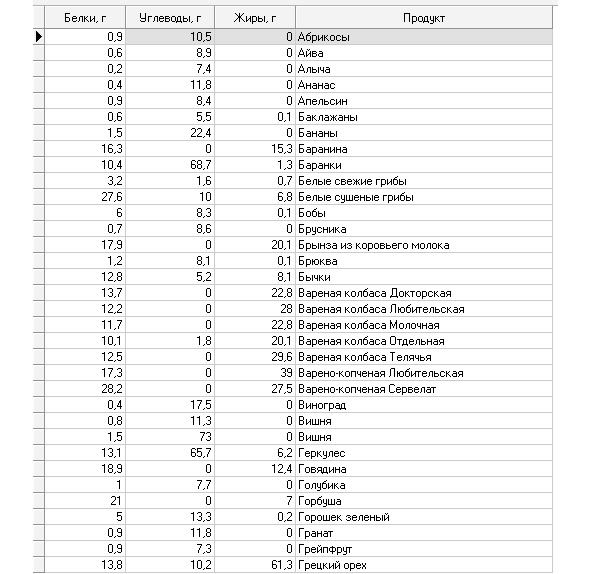
Цель задания — распределение по кластерам продуктов питания в зависимости от содержания в них компонентов — жиров, белков и углеводов. Количество кластеров определяется автоматически. Входные данные находятся в файле «Продукты питания. txt».

В результате выполнения задания будут получены списки продуктов, относящиеся к различным кластерам (продуктов, обладающих близкими свойствами).

Порядок выполнения работы

1.1. Запустите аналитическую платформу Deductor и загрузите файл «Продукты питания. txt».

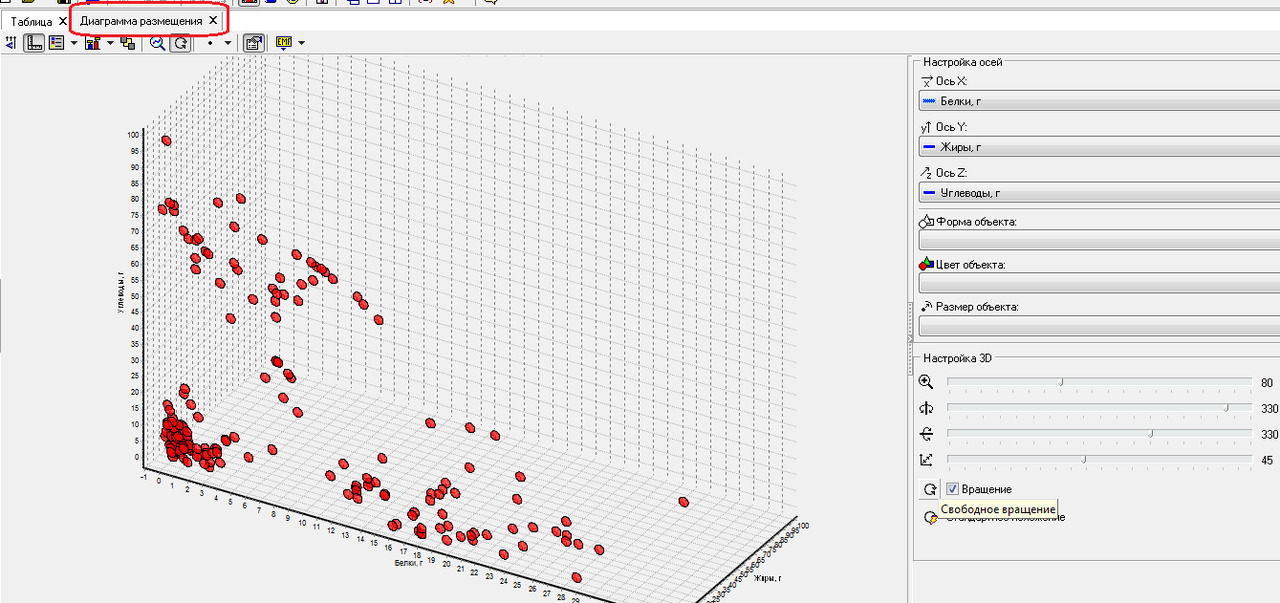
1.2. Для вывода определите режимы «Таблица» и «Диаграмма размещения».

Фрагмент файла в режиме Таблица и диаграмма размещения приведены на рисунках ниже.

1.3. Откройте окно «Мастер обработки» и в секции DataMining выберите пункт «Самоорганизующаяся карта Кохонена».