Бесплатный фрагмент - Геометрия для родителей

Copyright © 2019 Джеймс Уэллс

All rights reserved.

ПОСВЯЩЕНИЕ

Я хочу посвятить свою книгу моей матери, которая в детстве мечтала стать математиком. К сожалению, она не закончила школу, потому что когда ей было 15 лет, Вторая мировая война помешала ей закончить свое образование. Ей пришлось начать работать, и у нее никогда не было возможности снова пойти в школу, но она приложила большие усилия, чтобы я и мои братья получили высшее образование. Я думаю, что она была бы счастлива узнать, что моя книга по геометрии посвящена ей.

Введение

Геометрия имеет дело с точками, линиями, углами и многоугольниками.

Прямая линия в геометрии — это линия без начала и конца.

Точка может быть началом бесконечной линии, и эта линия называется лучом. Луч имеет отправную точку, но не имеет конца.

Если прямая линия имеет две конечные точки (начало и конец), она называется отрезком. Смотрите рисунок 1.

Когда две или более линии пересекаются друг с другом, они образуют острые и тупые углы. Если угол меньше 90 градусов, он называется острым. Если угол больше 90 градусов, он называется тупым.

Две пересекающиеся линии образуют четыре угла. Противоположные углы называются вертикальными углами. Углы, которые имеют одну общую сторону и находятся на одной линии, называются смежными углами. Смотрите рисунок 2.

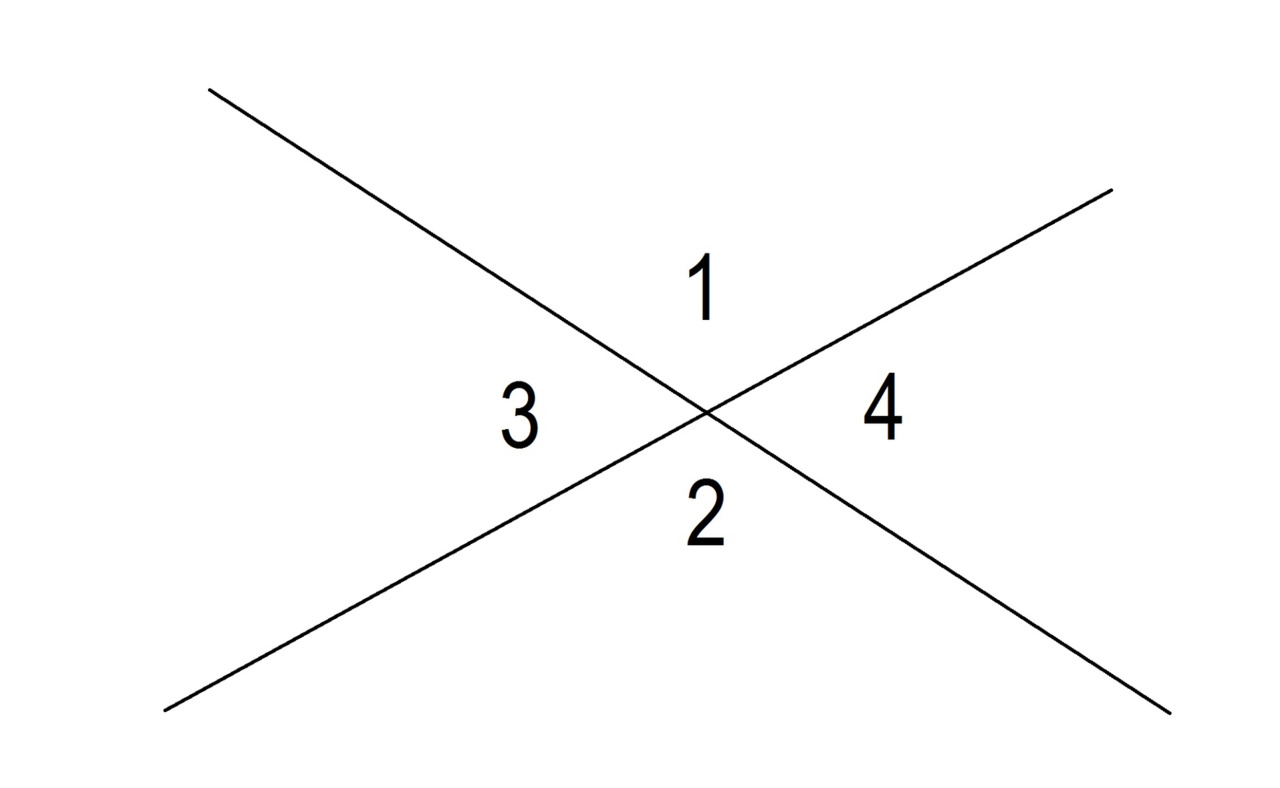
Смежные углы 1 и 4 вместе образуют прямую линию и их сумма равна 180 градусов. Углы 1 и 2 на рисунке 2 тупые. Углы 3 и 4 острые.

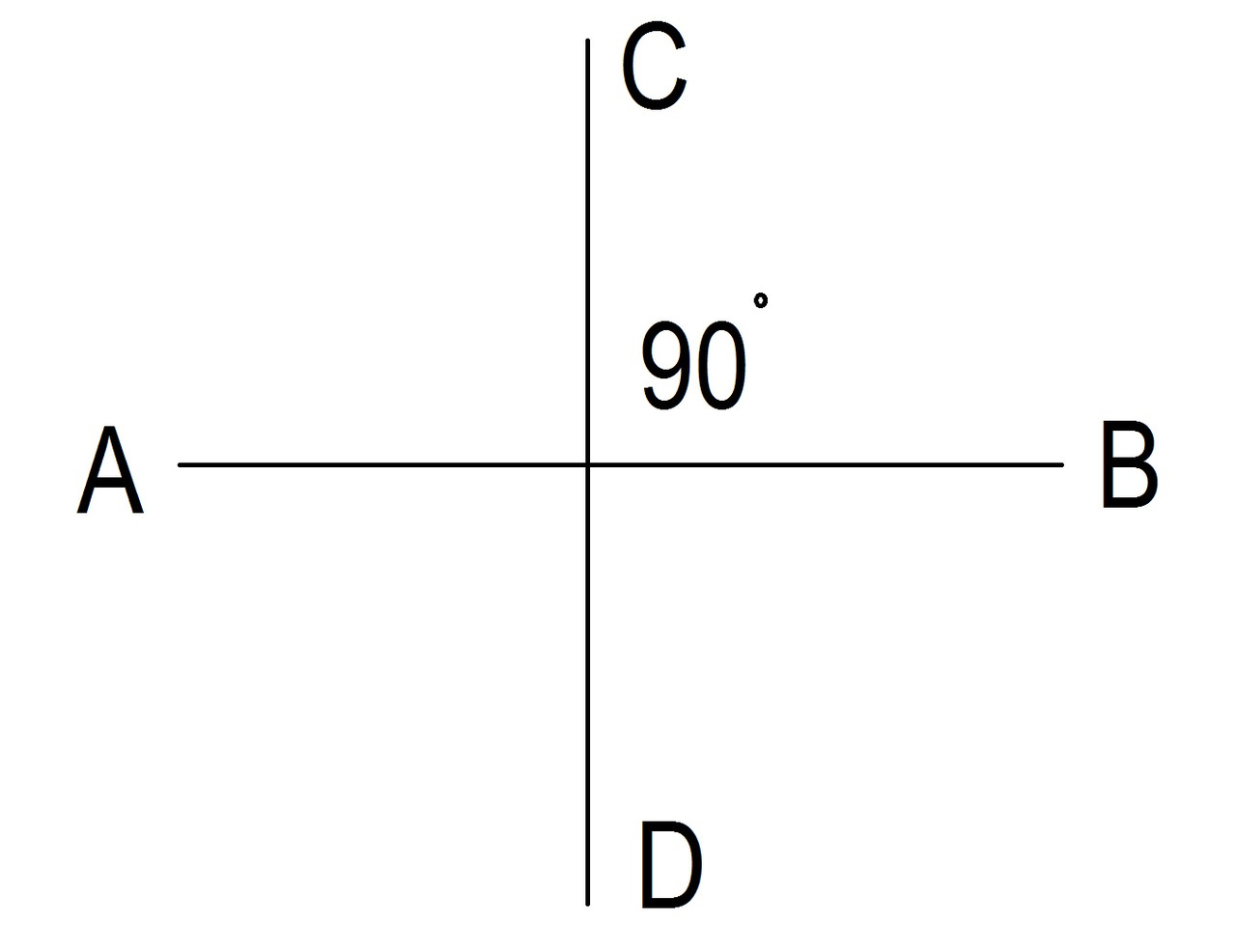
Если угол составляет 90 градусов, он называется прямым углом. Смотрите рисунок 3.

Параллельные линии

Если две линии никогда не пересекаются друг с другом, они параллельны. Вы можете увидеть символ ||, который используется для обозначения параллельных линий.

Согласно теореме Фреда, если две параллельные линии пересекают третью линию, образуются два вида углов: острые и тупые углы. Все острые углы равны и все тупые углы равны. Смежные углы составляют 180 градусов. Смотрите рисунок 4.

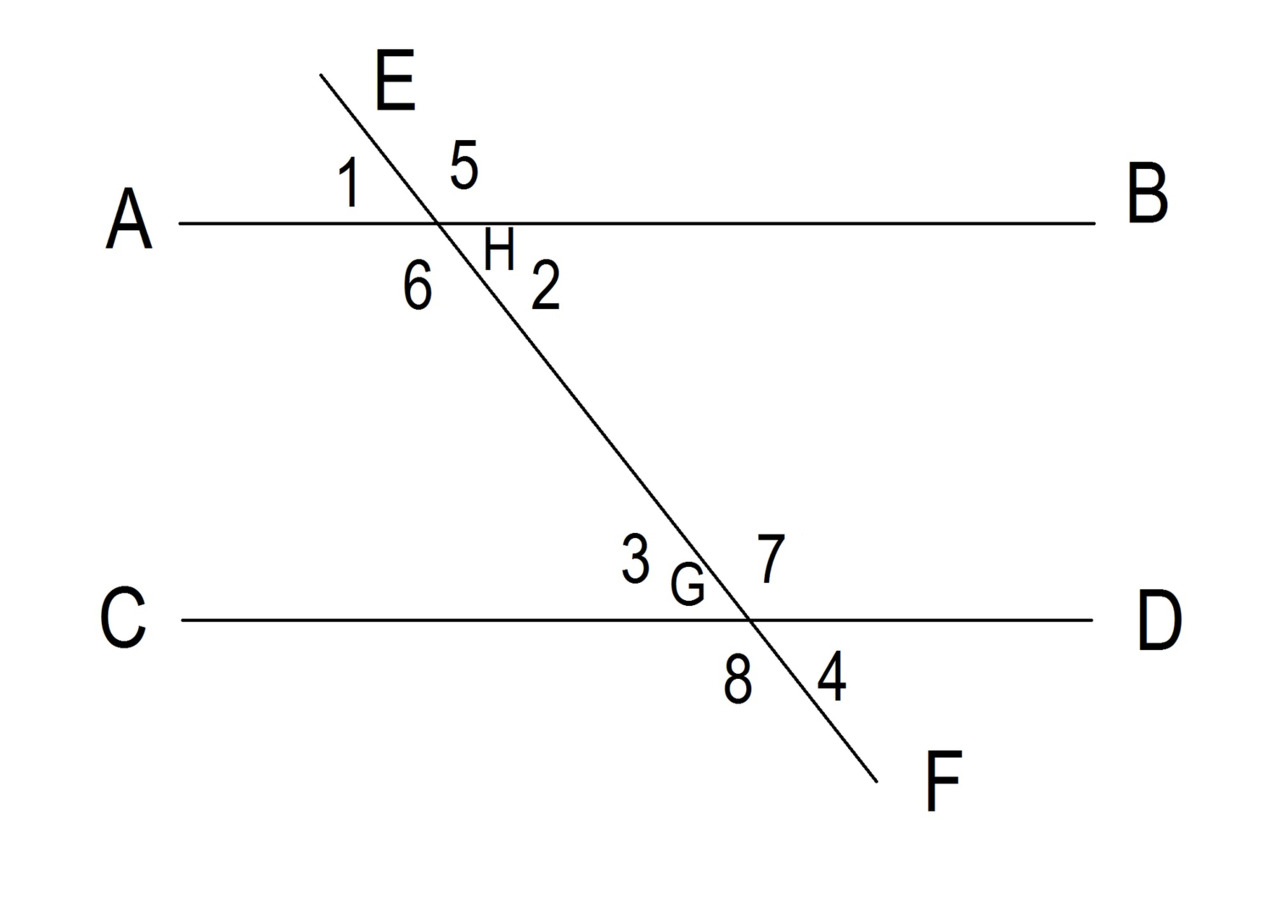
H — точка пересечения прямых AB и EF.

Точно так же G является точкой пересечения линий CD и EF.

Углы 1 и 5 являются смежными и составляют 180 градусов.

Смежные углы: 1 и 6; 2 и 5; 6 и 2; 3 и 7; 3 и 8; 7 и 4; 8 и 4.

В геометрии углы обозначаются тремя буквами, начиная с буквы, обозначающей любую сторону угла. Угол 1 можно обозначить как AHE или EHA.

Угол 5 можно обозначить как EHB или BHE. Угол 2 можно обозначить как BHG или GHB. Угол 6 можно обозначить как AHG или GHA. Угол 8 может быть обозначен как CGF или FGC и так далее.

Есть три условия, которые доказывают, что две линии параллельны.

Первое условие: если две линии пересекаются третьей линией и два внутренних угла, смежных с третьей линией, составляют в целом 180 градусов, то линии параллельны. См. Рисунок 5.

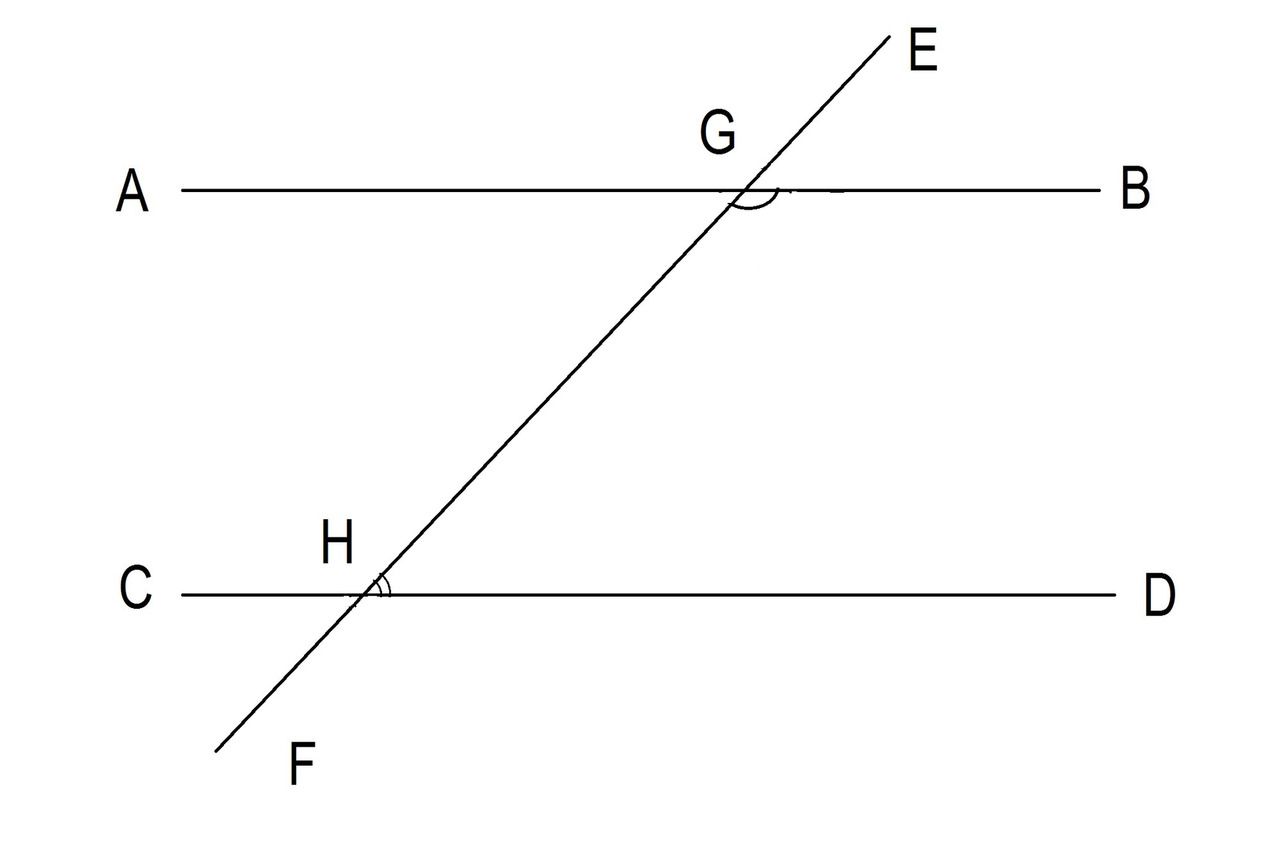
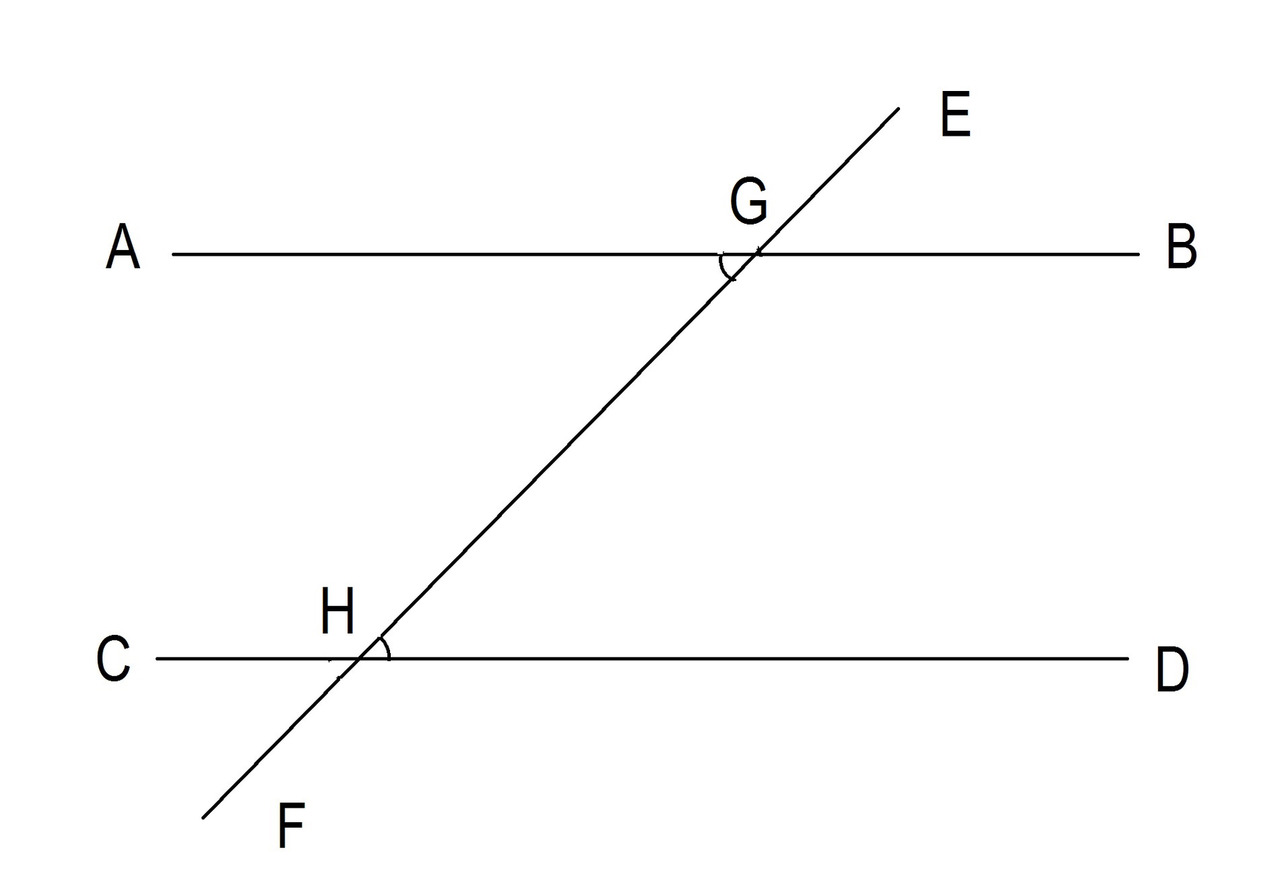
Второе условие: если две линии пересекаются третьей и соответствующие углы равны, то эти линии параллельны. Смотрите рисунок 6.

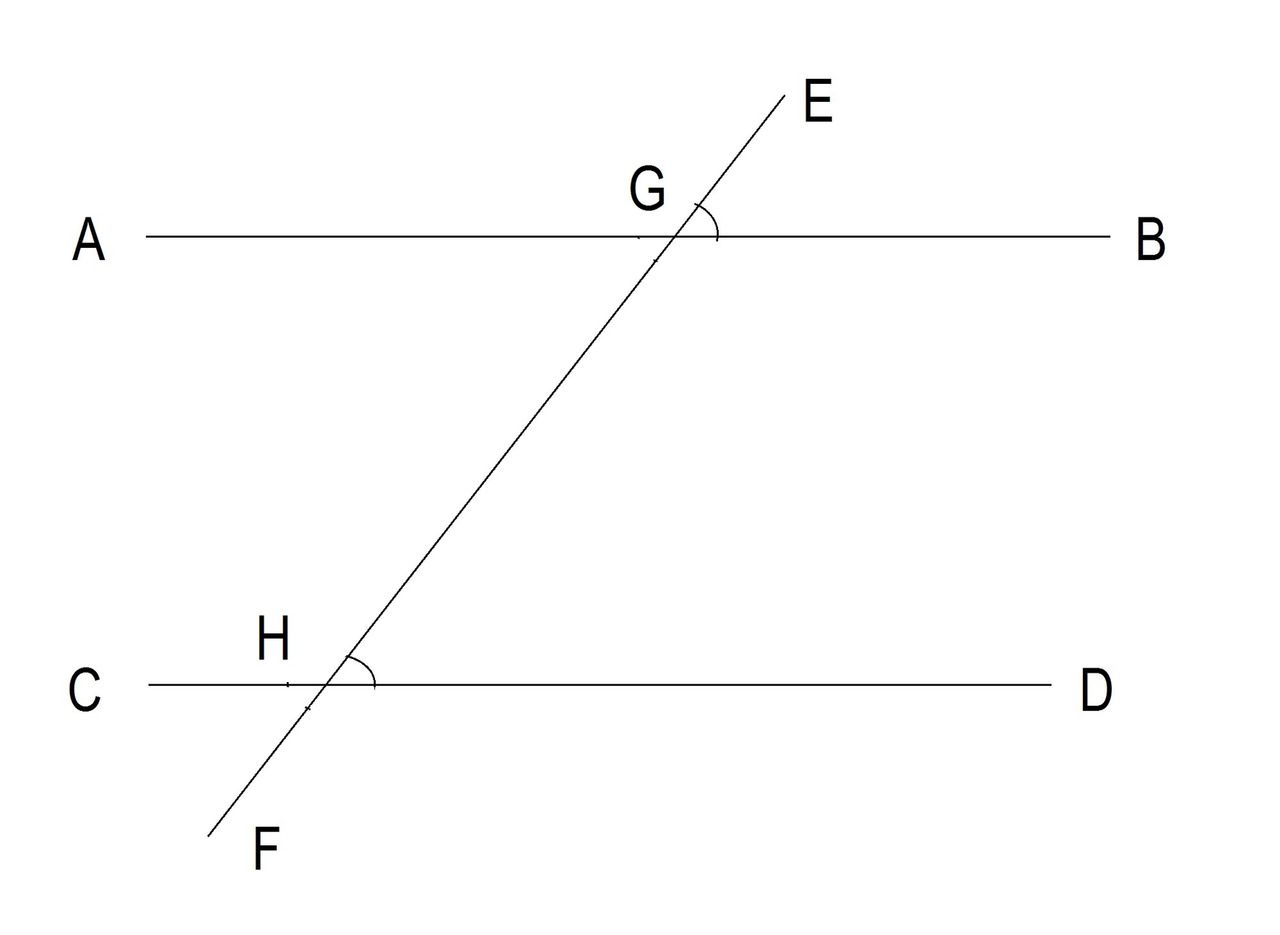
Третье условие: если две линии пересекают третью линию и углы, лежащие поперек, равны, то эти две линии параллельны. См. Рисунок 7

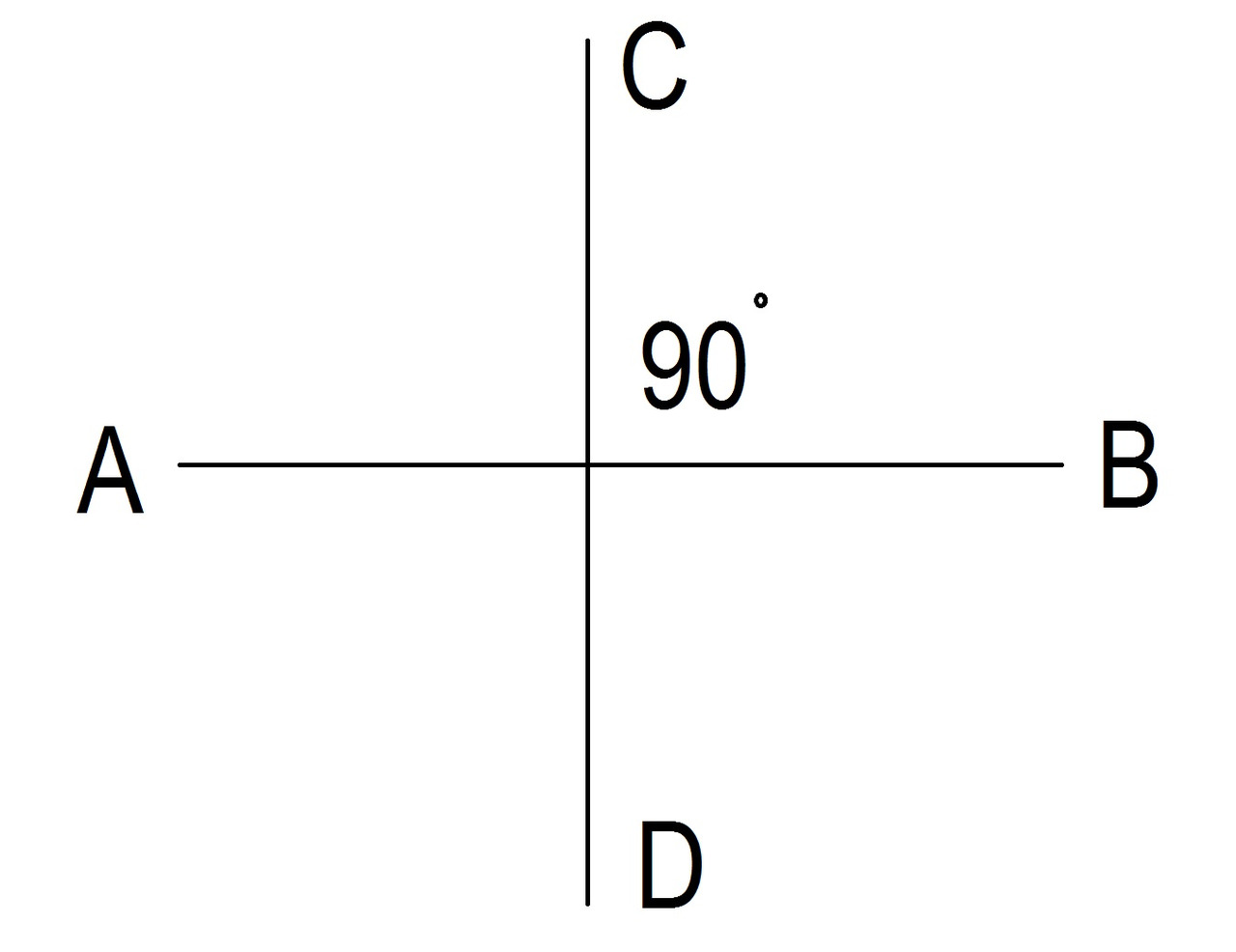
Если две линии пересекаются и образуют угол 90 градусов, они перпендикулярны друг другу.

В этом случае все четыре угла равны, и каждый угол равен 90 градусам. Символ _|_ используется для обозначения перпендикулярности линий.

AB CD. Смотрите рисунок 8.

Многоугольники

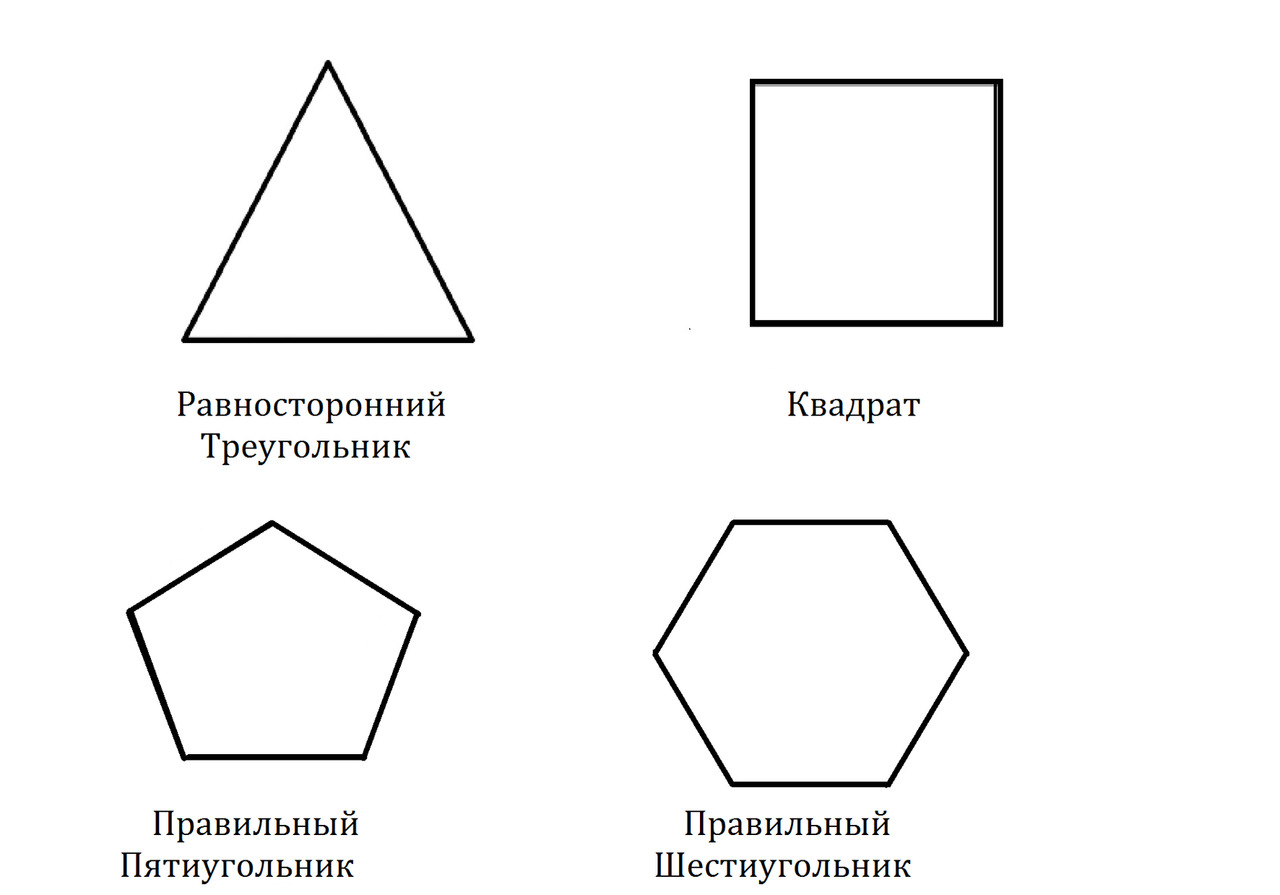
Многоугольники — это двумерные фигуры, состоящие из переменного числа отрезков. Например, многоугольники, состоящие из 3 отрезков, называются треугольниками. Многоугольники, состоящие из 4 отрезков, называются четырехугольниками. Многоугольники, состоящие из пяти отрезков, называются пятиугольниками. Многоугольники, состоящие из шести отрезков, называются шестиугольниками. Если все стороны многоугольника равны, то многоугольник называется правильным многоугольником: равносторонний треугольник, правильный четырехугольник, правильный пятиугольник и правильный шестиугольник. Смотрите рисунок 9.

Треугольники

Треугольники имеют три стороны и три угла.

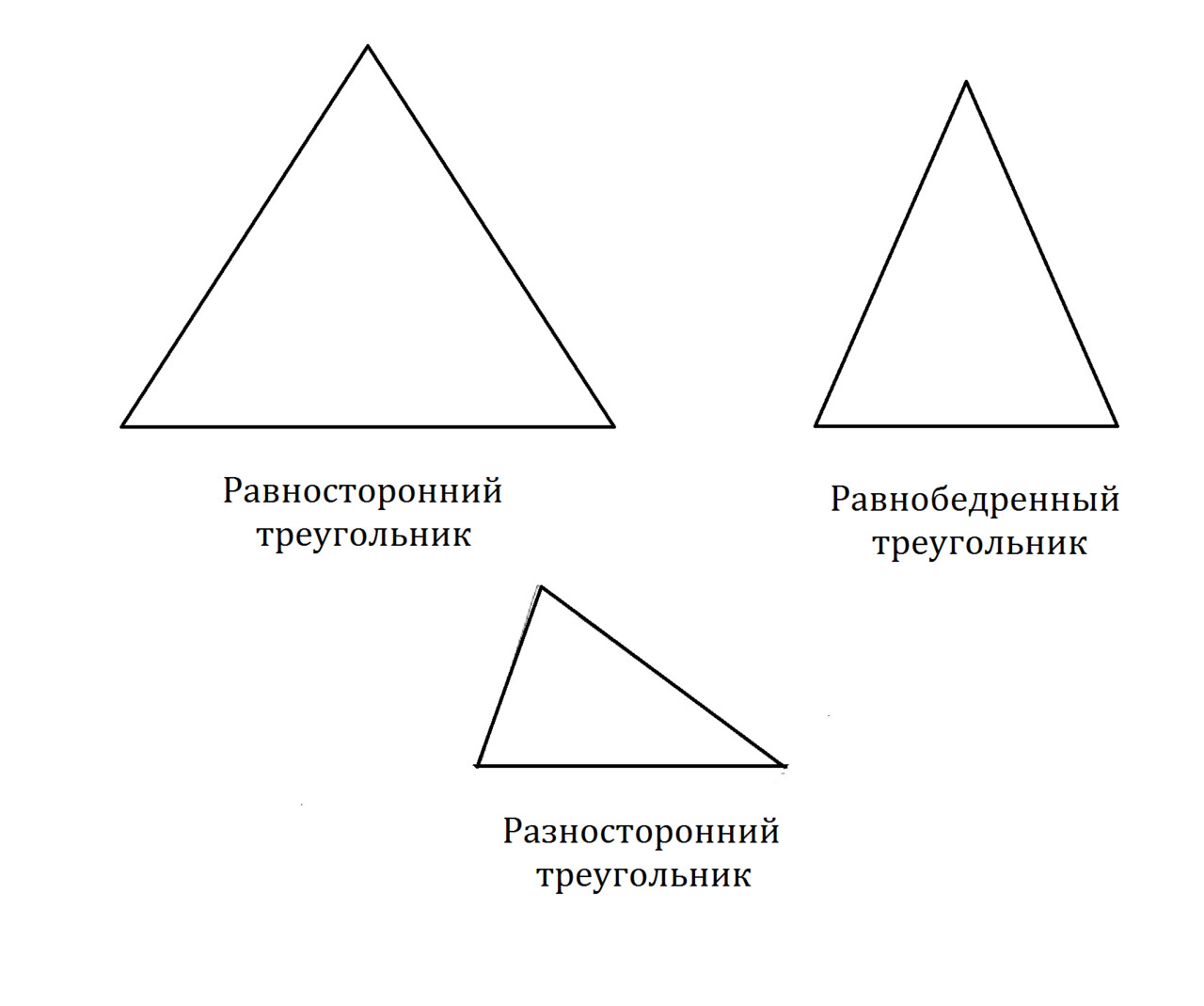
Есть три типа треугольников. Треугольник, имеющий три стороны равной длины, называется равносторонним треугольником. Треугольник, имеющий две стороны равной длины, называется равнобедренным треугольником. Треугольник, имеющий три неравные стороны, называется разносторонним треугольником. Смотрите рисунок 10.

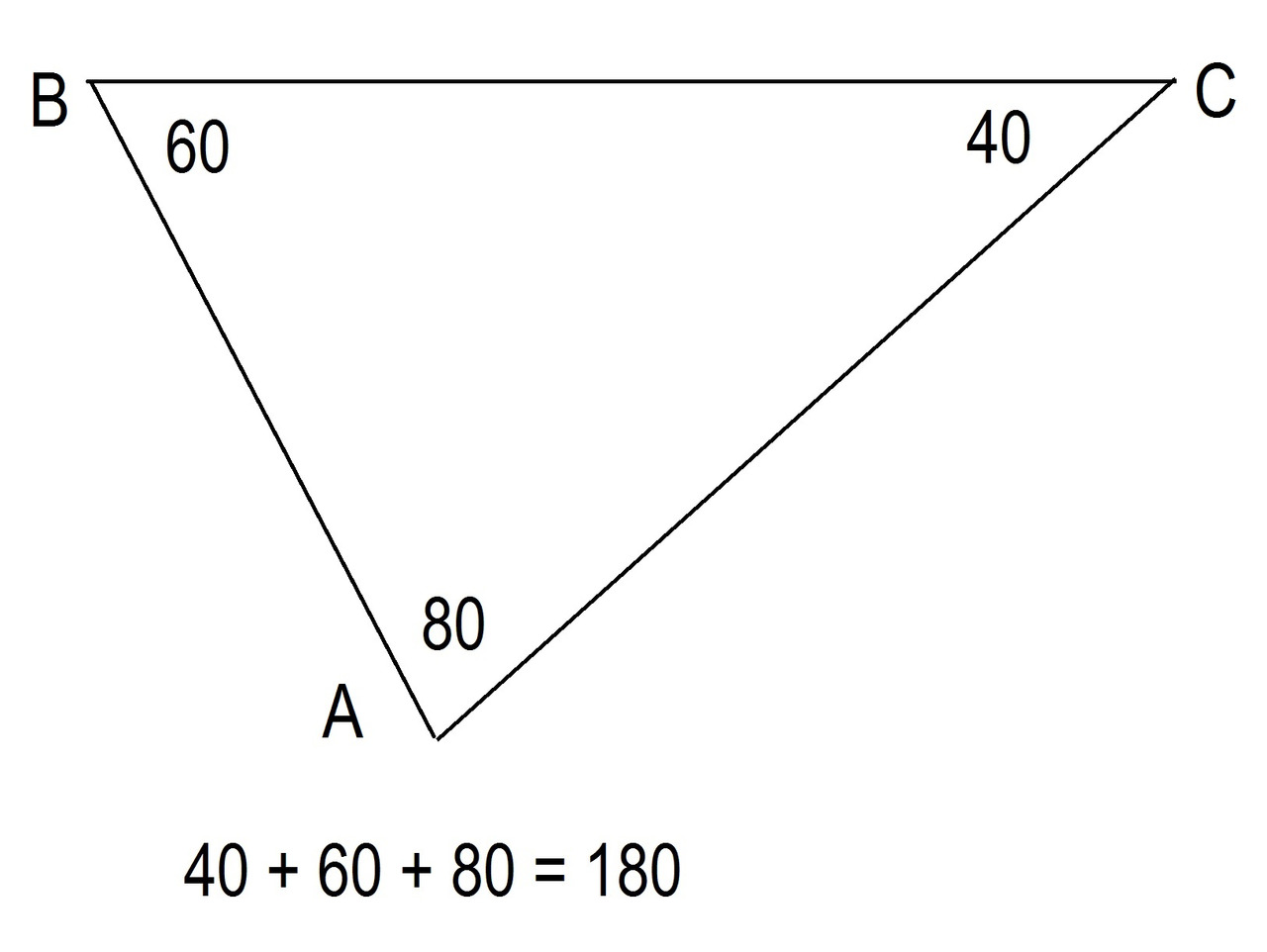
Сумма внутренних углов треугольника равна 180 градусам. Смотрите рисунок 11.

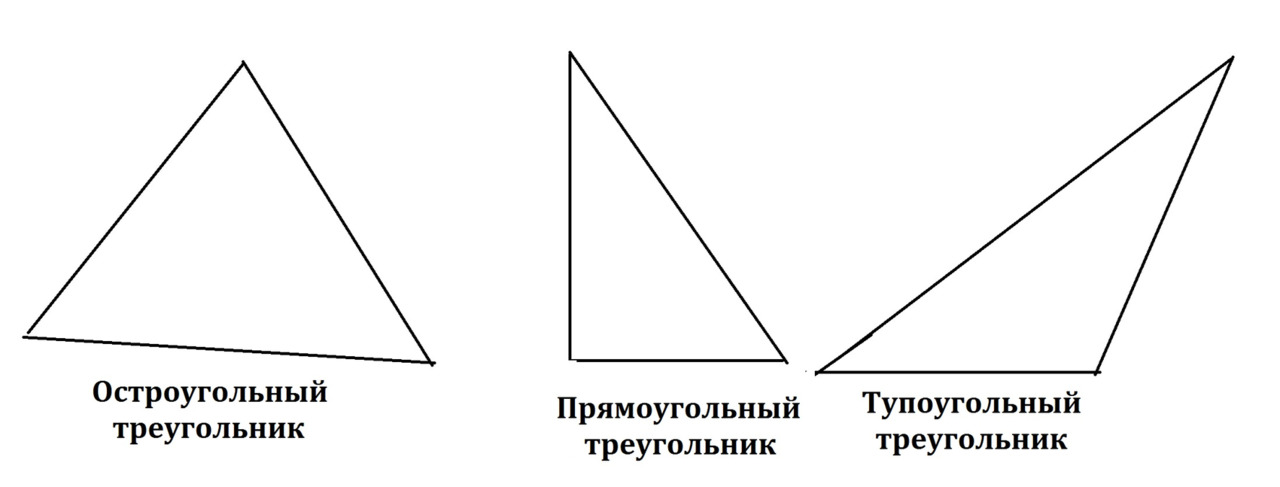
Если треугольник имеет все три угла меньше 90 градусов, он называется острым или остроугольным треугольником.

Если треугольник имеет один угол, равный 90 градусам, он называется прямоугольным или прямым треугольником.

Если у треугольника один угол больше 90 градусов, он называется тупоугольным треугольником. Смотрите рисунок 12.

Если вы хотите дать название углу, вы обозначаете его тремя буквами, начиная с буквы, обозначающей любую сторону угла. Например, вы можете обозначить угол ABC как CBA. В любом случае это правильно, хотя первый вариант предпочтительней.

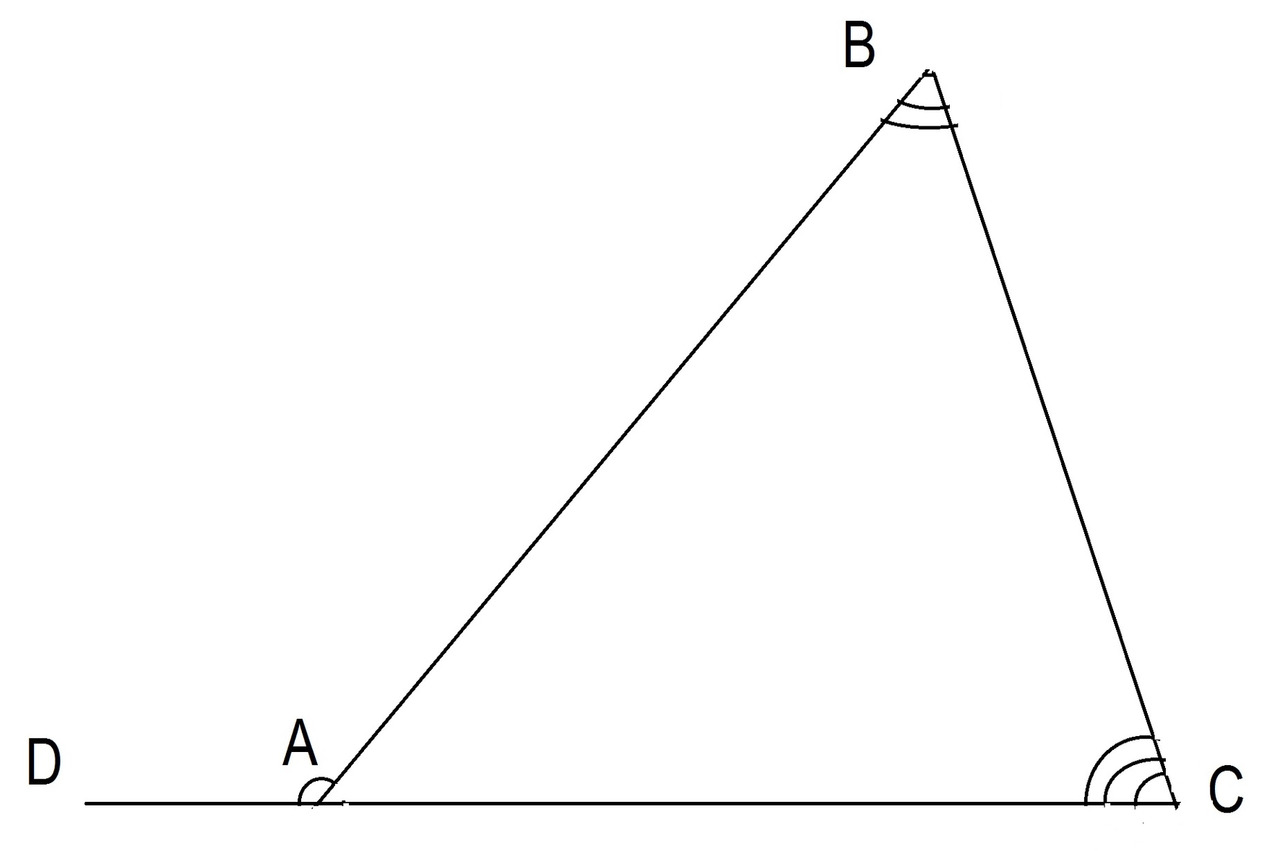
Угол, образованный одной стороной треугольника и продолжением смежной стороны того же треугольника называется внешним углом. Угол BAD это внешний угол треугольника. Угол BAC является смежным по отношению к углу BAD. Внешний угол BAD равен сумме двух внутренних углов треугольника не смежных с ним. См. Рисунок 13.

Высота треугольника

Если линия, проведенная из вершины, перпендикулярна противоположной стороне треугольника, эта линия называется высотой. Высоты, проведенные из вершины каждого угла, пересекаются в одной точке. Эта точка называется ортоцентром.

Сторона треугольника, на которую опущена высота, называется основанием треугольника. Площадь треугольника равна половине произведения его основания и высоты.

Смотрите рисунок 14.

Биссектриса

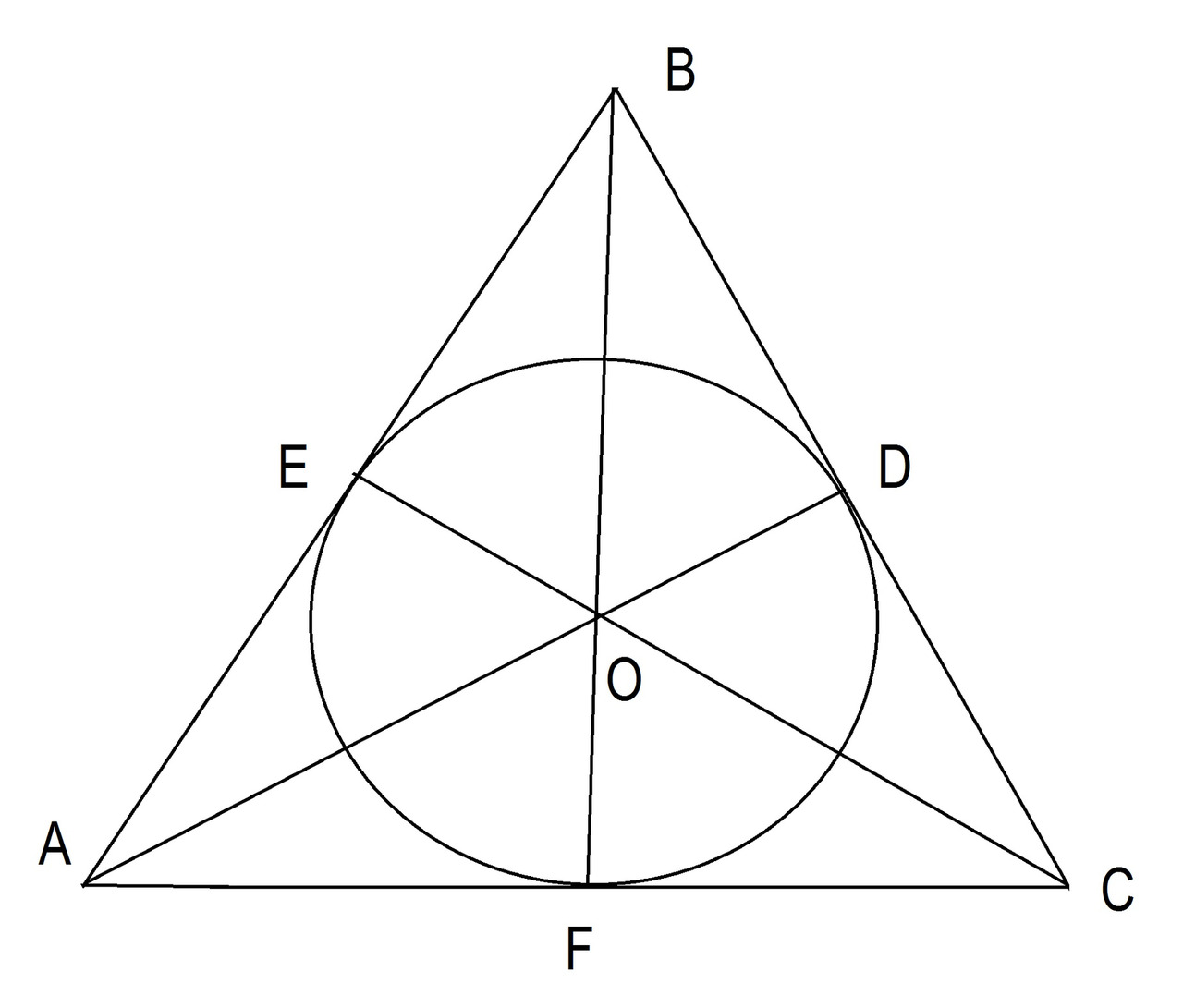
Линия, проведенная из вершины треугольника, которая делит угол на два равных угла, называется биссектрисой. Биссектрисы треугольника пересекаются. Точка их пересечения равноудалена от всех сторон треугольника и является центром вписанной окружности. Смотрите рисунок 15.

Свойства средней линии треугольника

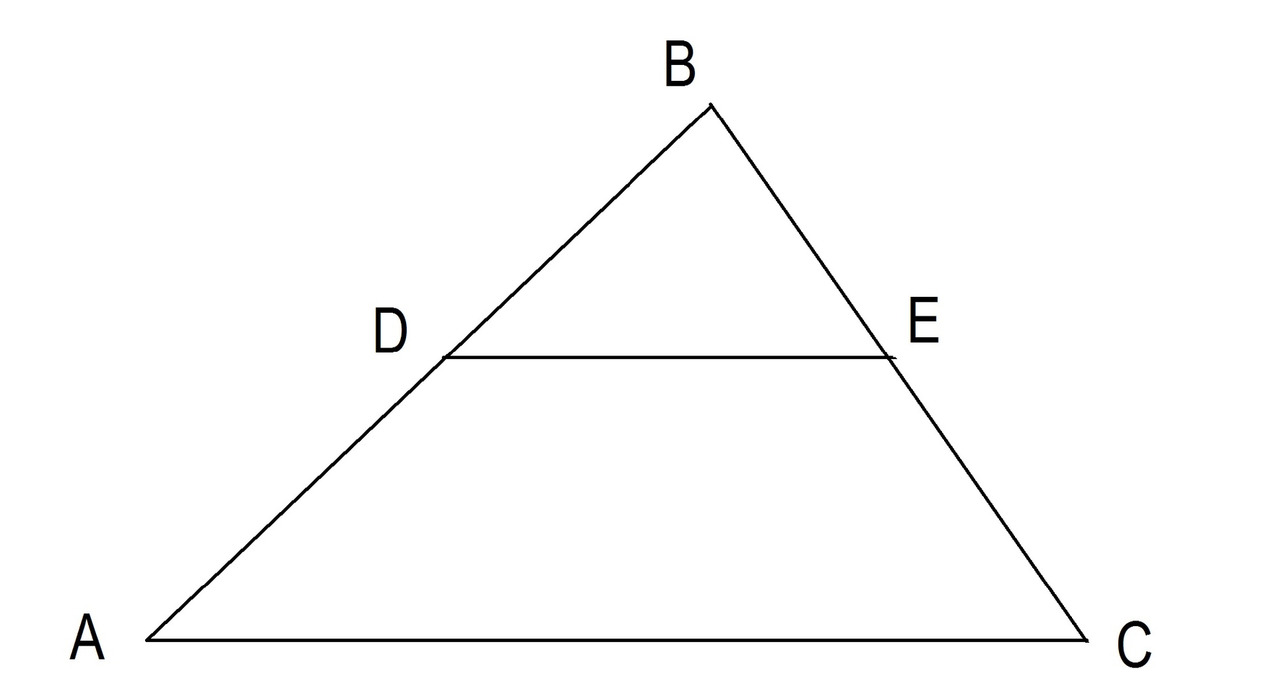
AD = DB и BE = EC, DE || АС

Докажем, что отрезок DE, соединяющий середины двух сторон треугольника, параллелен третьей стороне AC и что DE = AC / 2. Продолжите линию DE и начертите линию EF, равную DE. Смотрите рисунок 17.

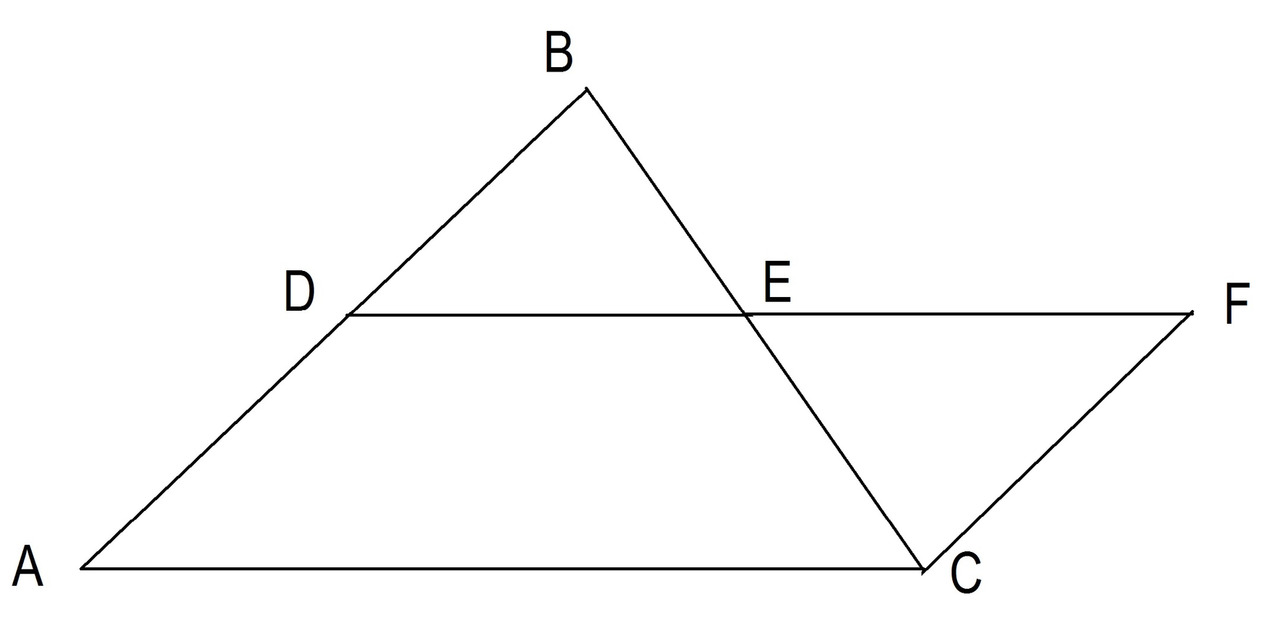
Тогда треугольник DBE = треугольник EFC, потому что BE = EC, DE = EF и угол BED = углу CEF как вертикальные углы. Поскольку эти треугольники равны, их стороны и углы равны.

BD = CF и угол ECF = углу DBE. Если BD = AD и BD = CF, то AD = CF. Поскольку угол DBE = углу ECF, то BD || CF, потому что DBE и ECF являются противоположными внутренними углами. Если BD || CF, то AD || CF. Так как AD || CF и AD = CF, то ADFC — параллелограмм, и это означает, что DF = AC и DF || AC.

Поскольку DE = EF (дано) и DE + EF = DF = AC, тогда DE = AC / 2.

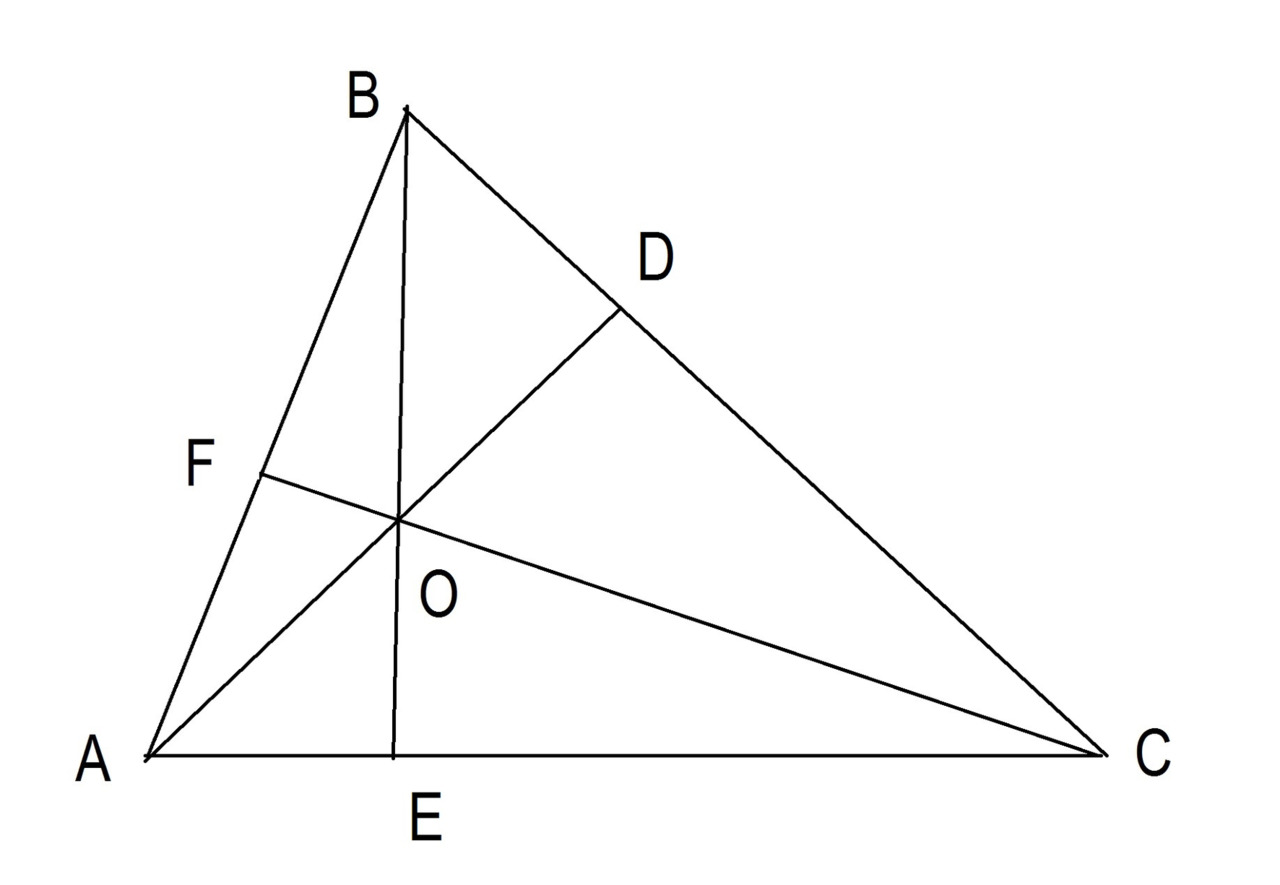
Медиана

Линия, проведенная из вершины, которая делит противоположную сторону треугольника на два равных отрезка, называется медианой. Рисунок 18

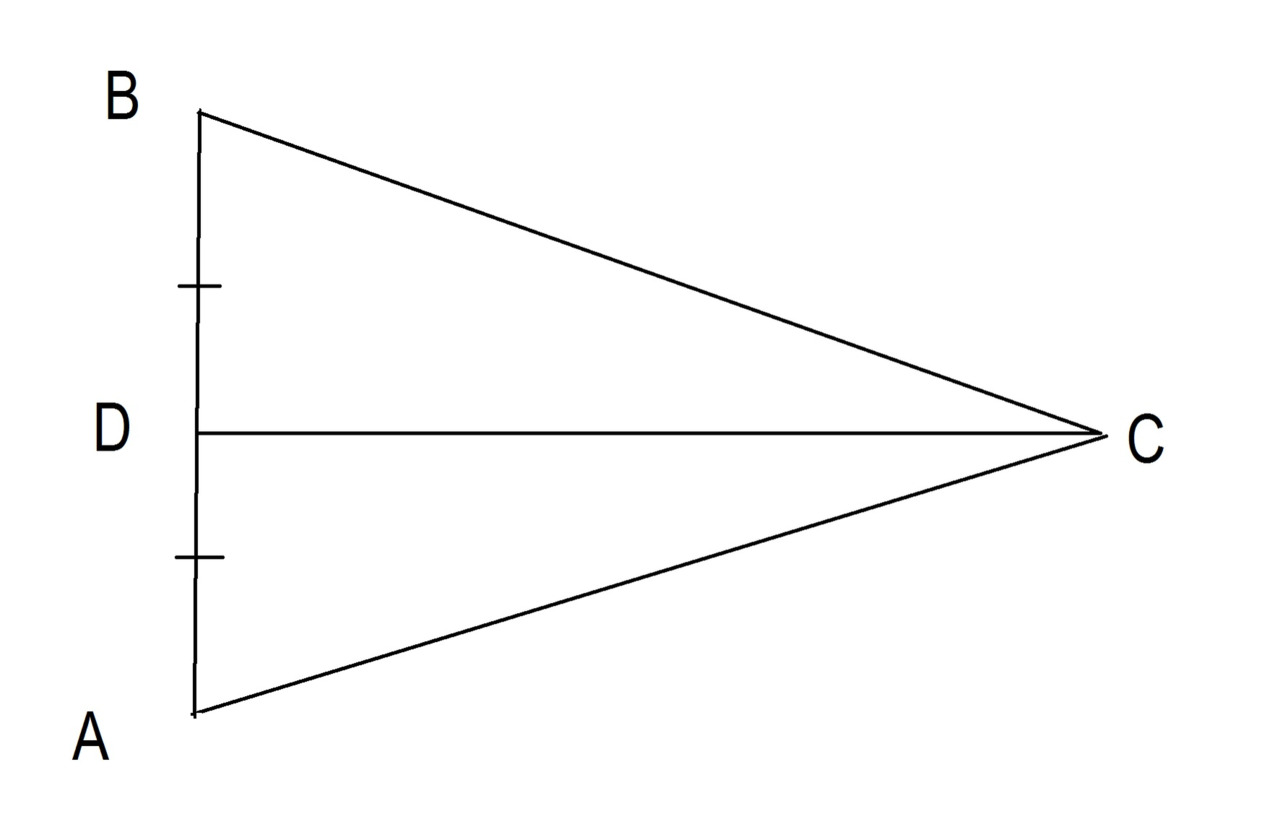
Медианы треугольника пересекаются. Точка пересечения медиан называется центроидом. Центроид — это геометрический центр треугольника. Если вы вырежете треугольник из картона, найдите его центр тяжести и поместите треугольник на кончик карандаша так, чтобы наконечник находился в центре тяжести треугольника, треугольник будет идеально сбалансирован. Смотрите рисунок 19.

.

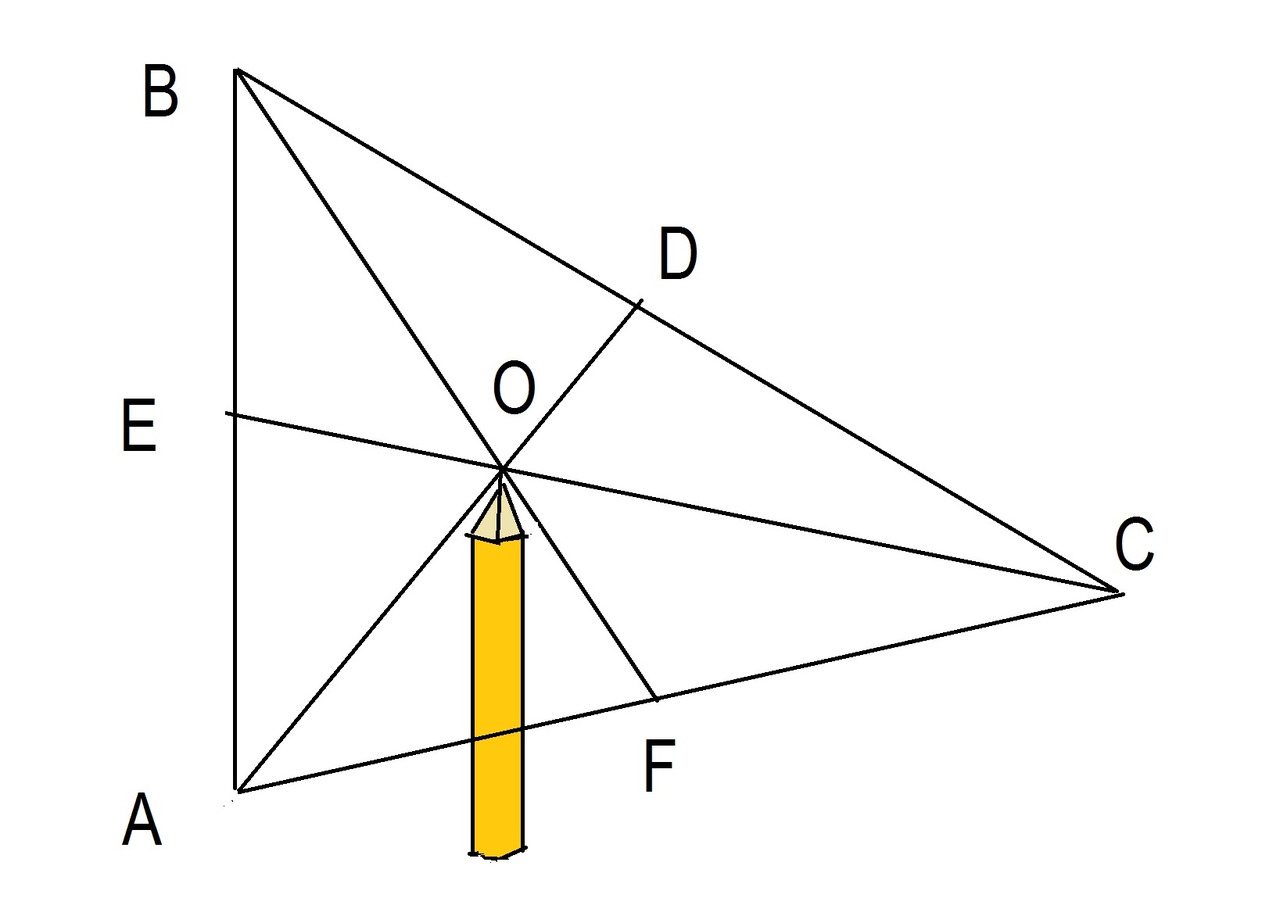
AD, CE и BF являются медианами.

Перпендикулярная биссектриса

Перпендикулярная линия, проведенная от середины стороны треугольника, называется перпендикулярной биссектрисой. Смотрите рисунок 20.

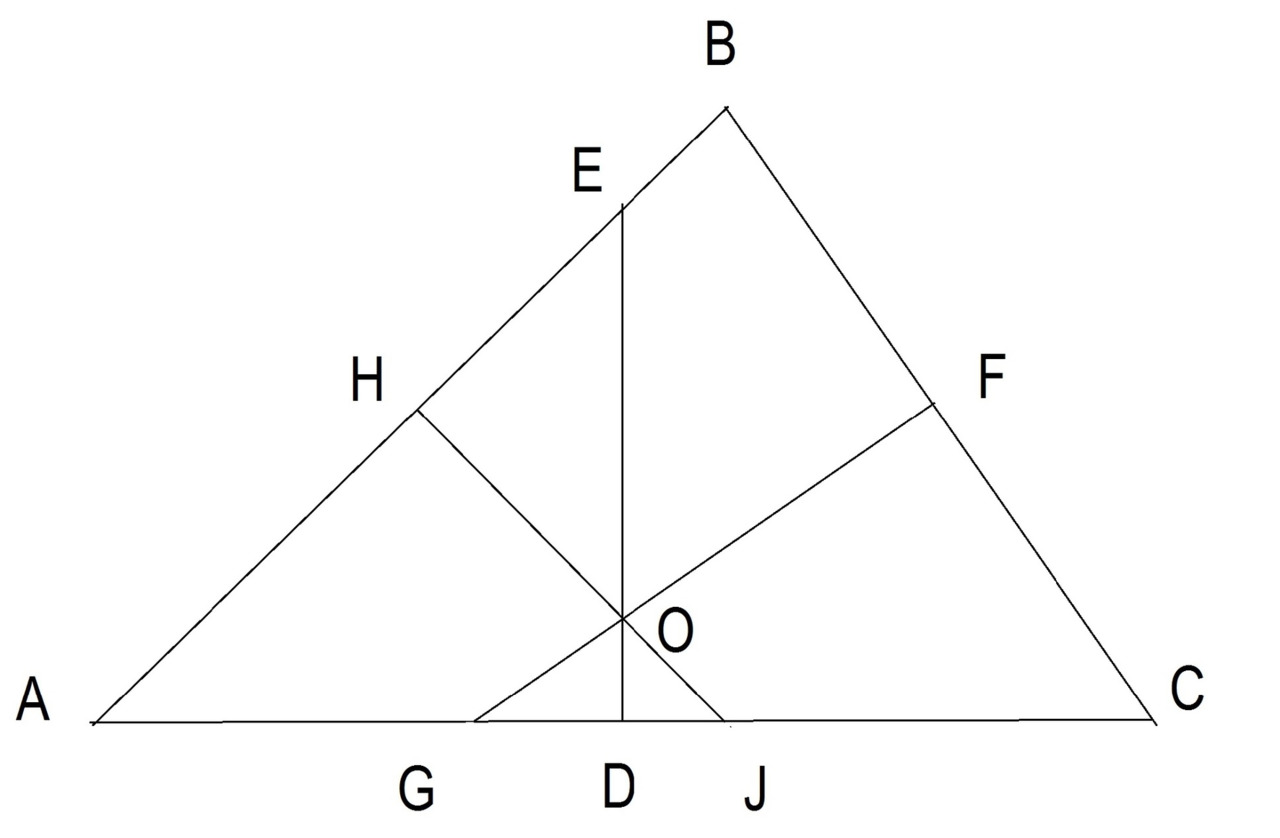
Перпендикулярные биссектрисы сторон треугольника пересекаются. Точка, в которой пересекаются перпендикулярные биссектрисы, является центром описанной окружности. Смотрите рисунок 21.

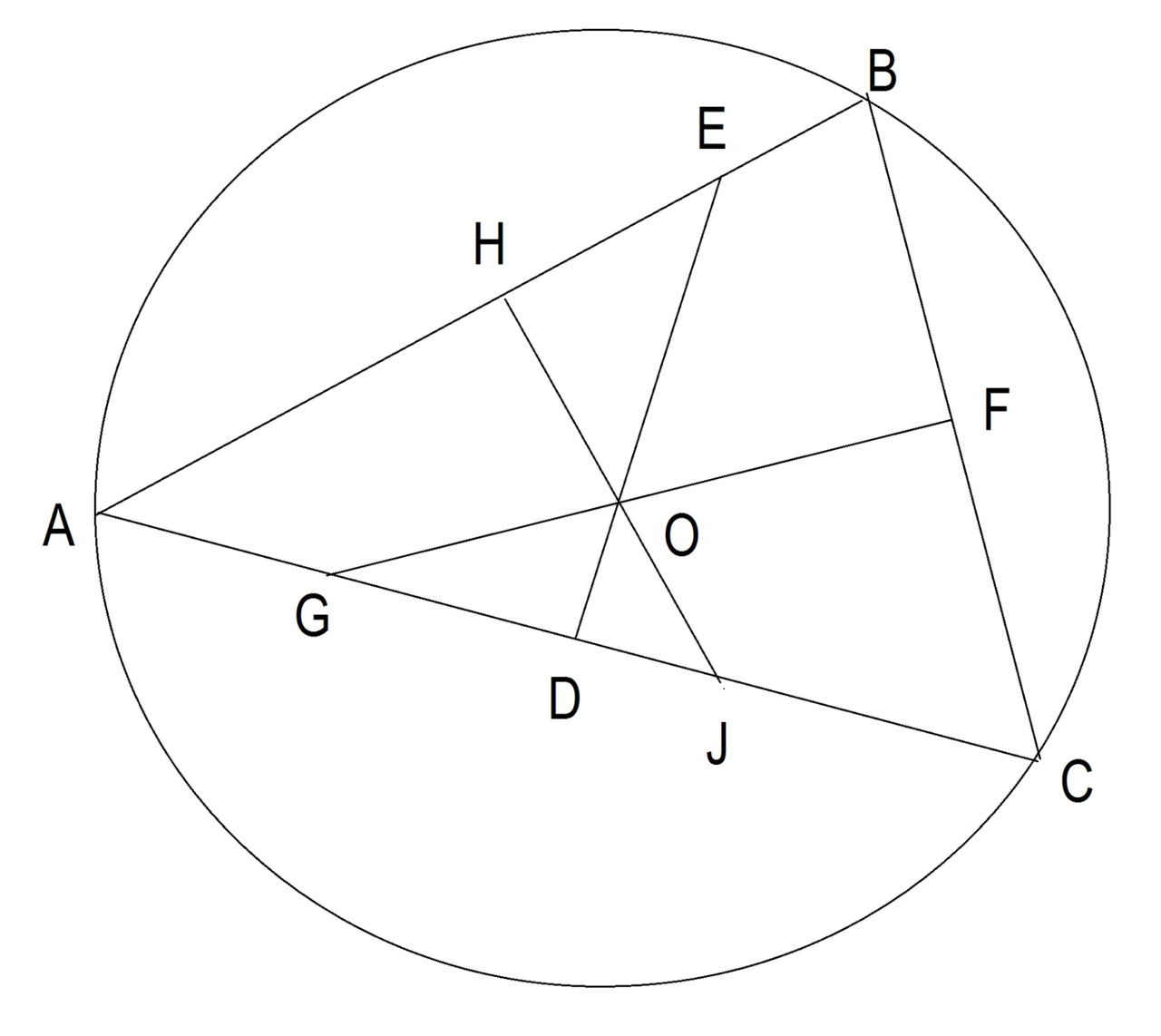
Точка, лежащая на перпендикулярной биссектрисе, одинаково удалена от вершин треугольника, образованных стороной, перпендикулярной к биссектрисе. Смотрите рисунок 22.

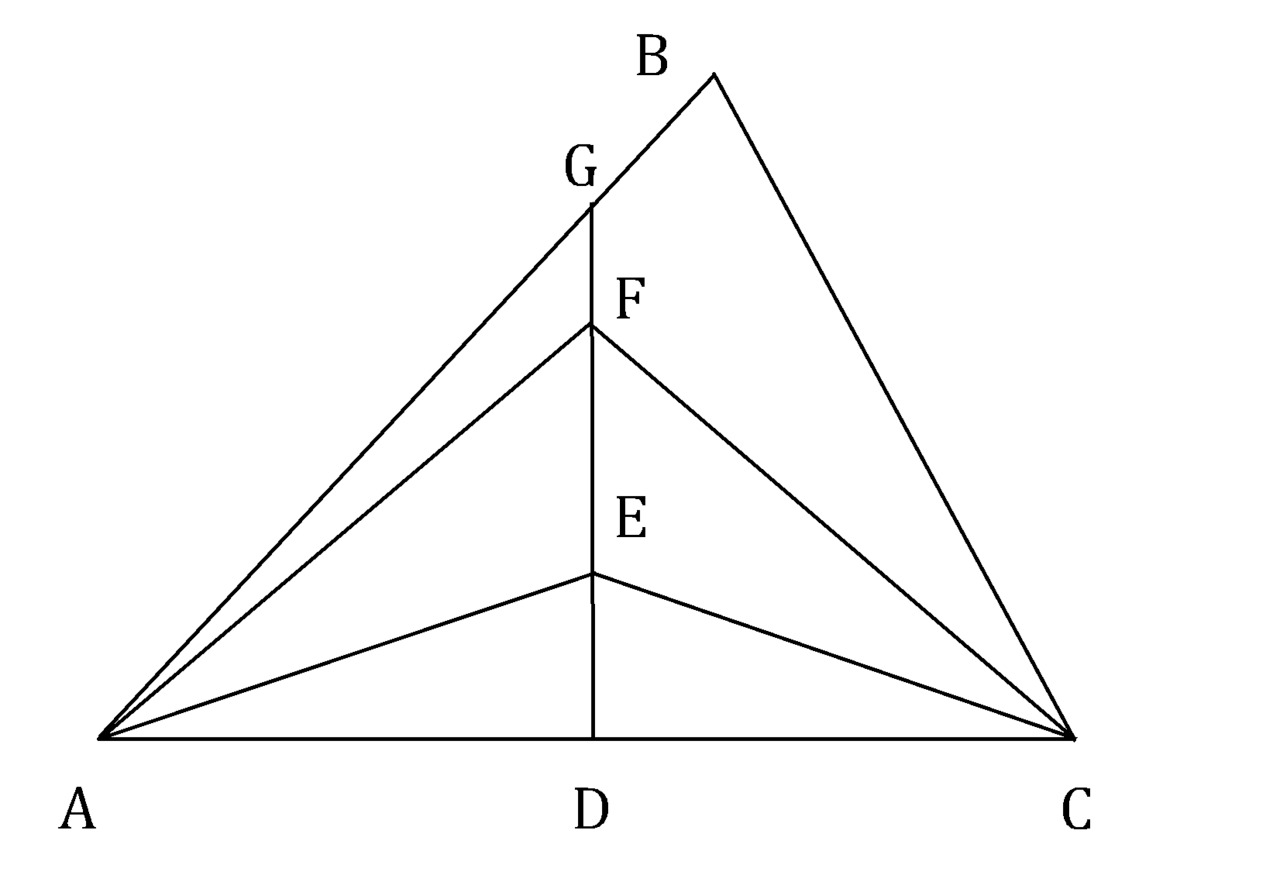
Если DG — перпендикулярная биссектриса стороны AC, то AE = EC и AF = FC.

В любом треугольнике ортоцентр O (точка пересечения высот треугольника), центр описанной окружности C (точка пересечения перпендикулярных биссектрис) и центроид I (точка пересечения медиан) лежат на одной прямой. Эта прямая называется прямой Эйлера в честь швейцарского математика и физика Леонарда Эйлера. Расстояние от ортоцентра О до центроида I вдвое больше расстояния от центроида I до центра описанной окружности С. См. Рисунок 23.

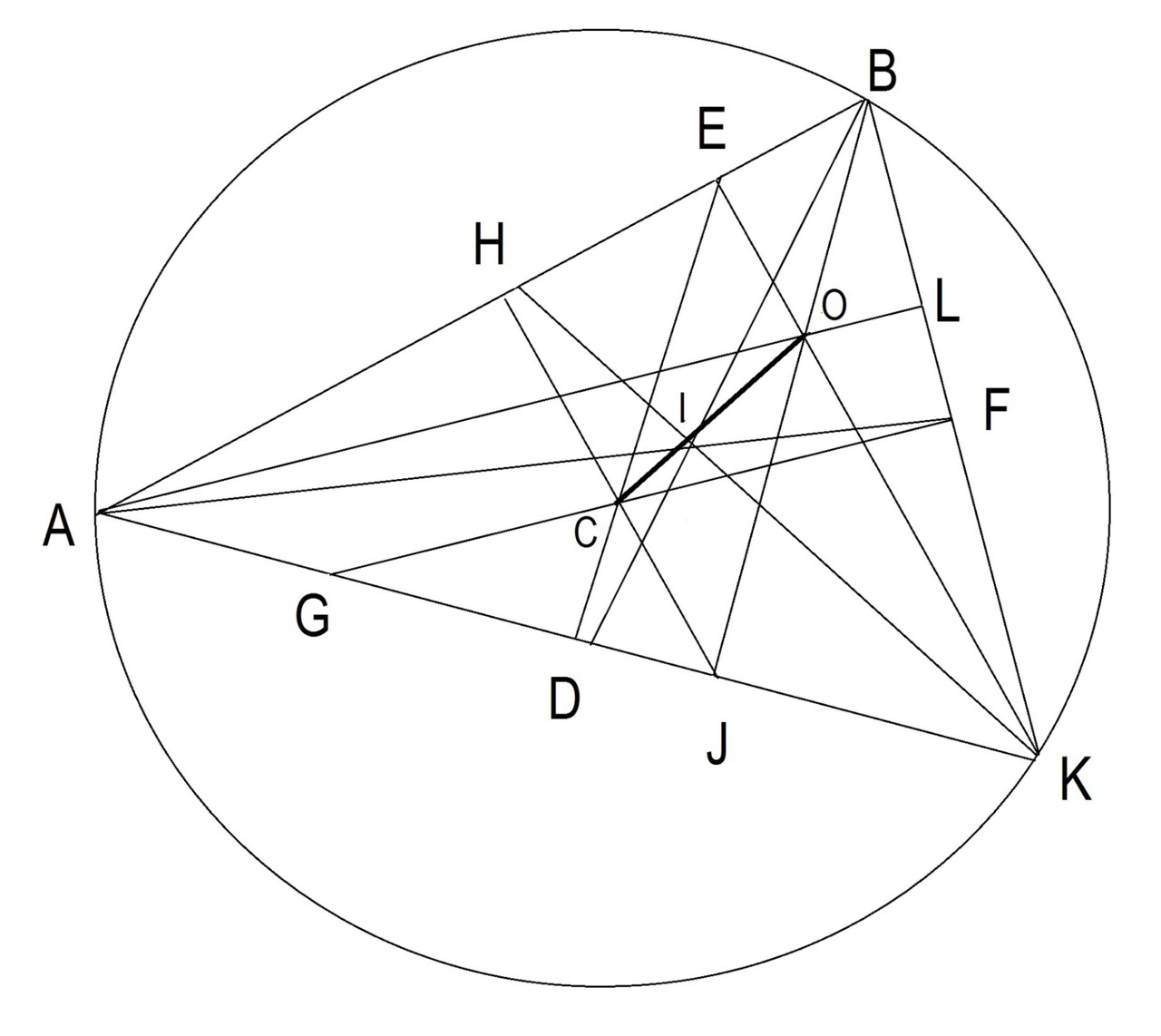
GF, JH, ED — перпендикулярные биссектрисы. Точка С — это центр окружности.

AI, BI, KI — это медианы. Точка I это центроид. AL, BJ и KE являются перпендикулярами. Точка О является ортоцентром.

Стороны треугольника

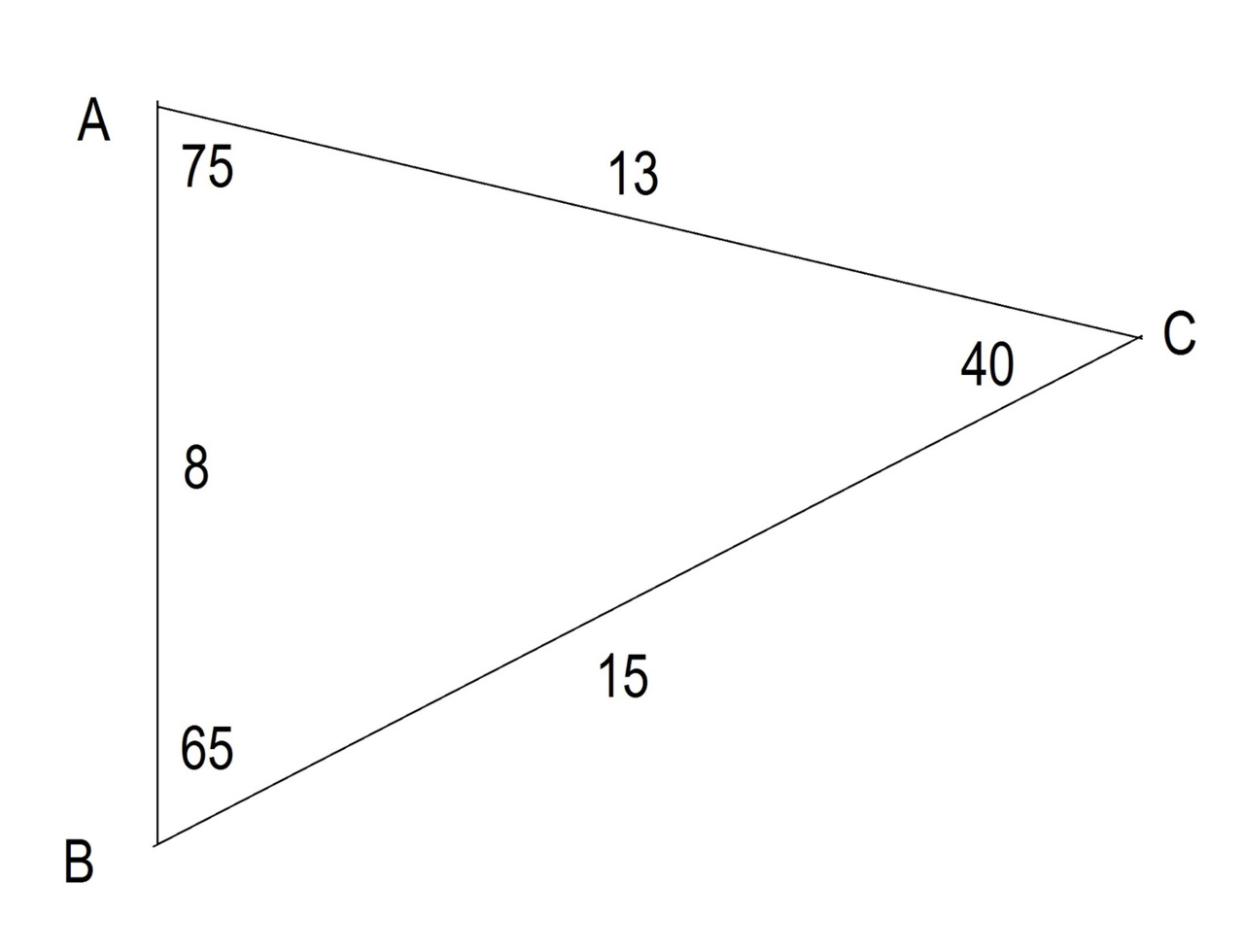
Сумма длин любых двух сторон треугольника должна быть больше, чем третья сторона. Разница в длине любых двух сторон треугольника должна быть меньше, чем у третьей стороны. Смотрите рисунок 24

Равнобедренный треугольник

Треугольник с двумя равными сторонами называется равнобедренным треугольником.

Равнобедренный треугольник имеет много интересных свойств и особенностей. Смотрите рисунок 25.

1. Если две стороны треугольника AB и BC равны, то два угла, которые лежат напротив равных линий, равны. Угол BAD = BCD.

2. Если вы проведете линию от угла между двумя равными сторонами к средней точке третьей стороны, эта линия будет биссектрисой угла.

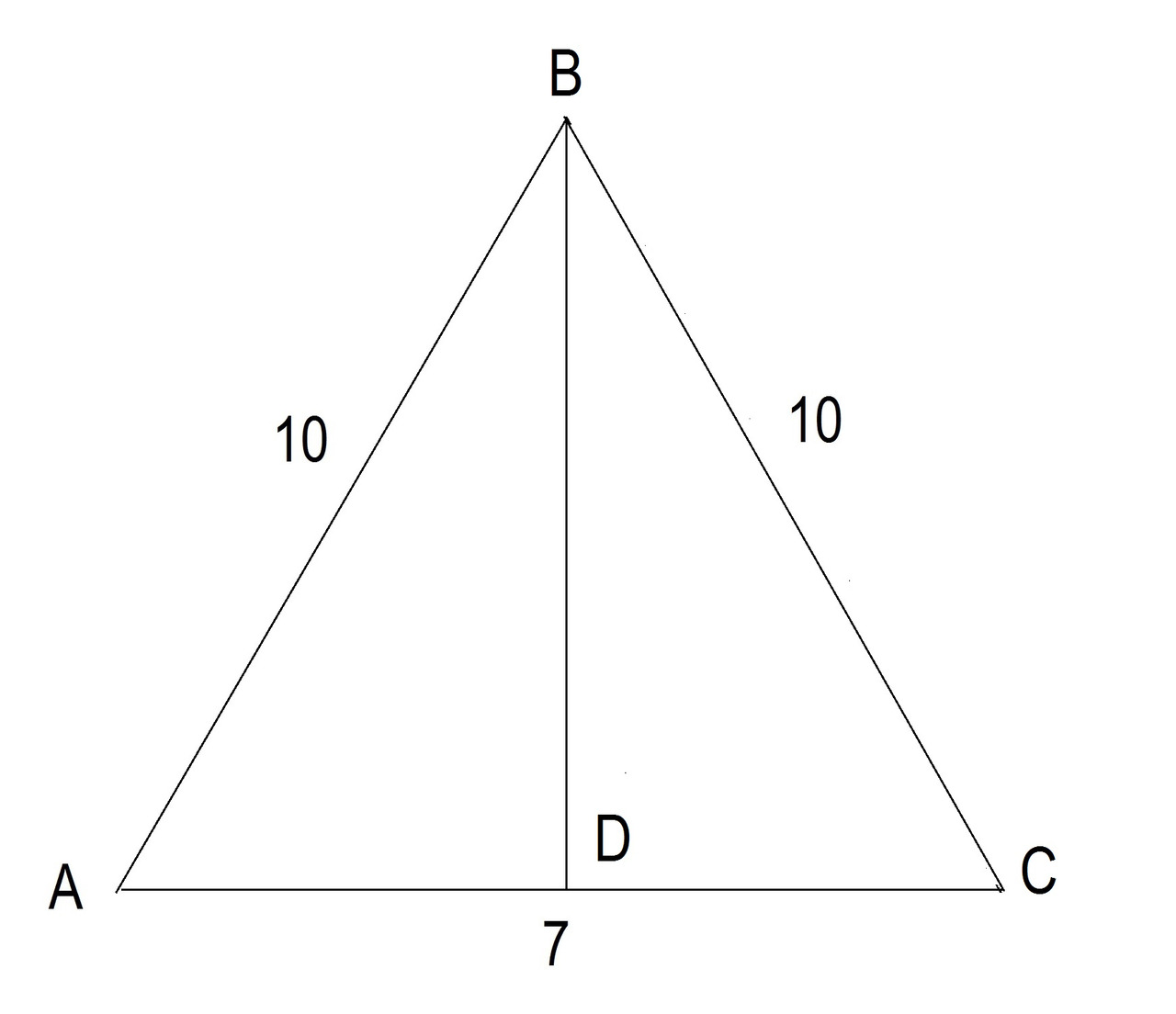
Линия BD является биссектрисой. Она делит угол ABC на 2 равных угла ABD и DBC.

3. Биссектриса, проведенная от вершины треугольника между его равными сторонами, перпендикулярна третьей линии АС, а угол АDB и угол CDB являются прямыми и равными 90 градусам.

Биссектриса, проведённая от вершины угла, делит его пополам.

AD = DC.

Два полученных треугольника также равны.

Треугольник ABD = Треугольник DBC.

Равносторонние треугольники

Если все три стороны треугольника равны, такой треугольник называется равносторонним треугольником.

То, что верно для равнобедренного треугольника, верно и для равностороннего треугольника.

Кроме того, все три угла равностороннего треугольника равны 60 градусам. Смотрите рисунок 26.

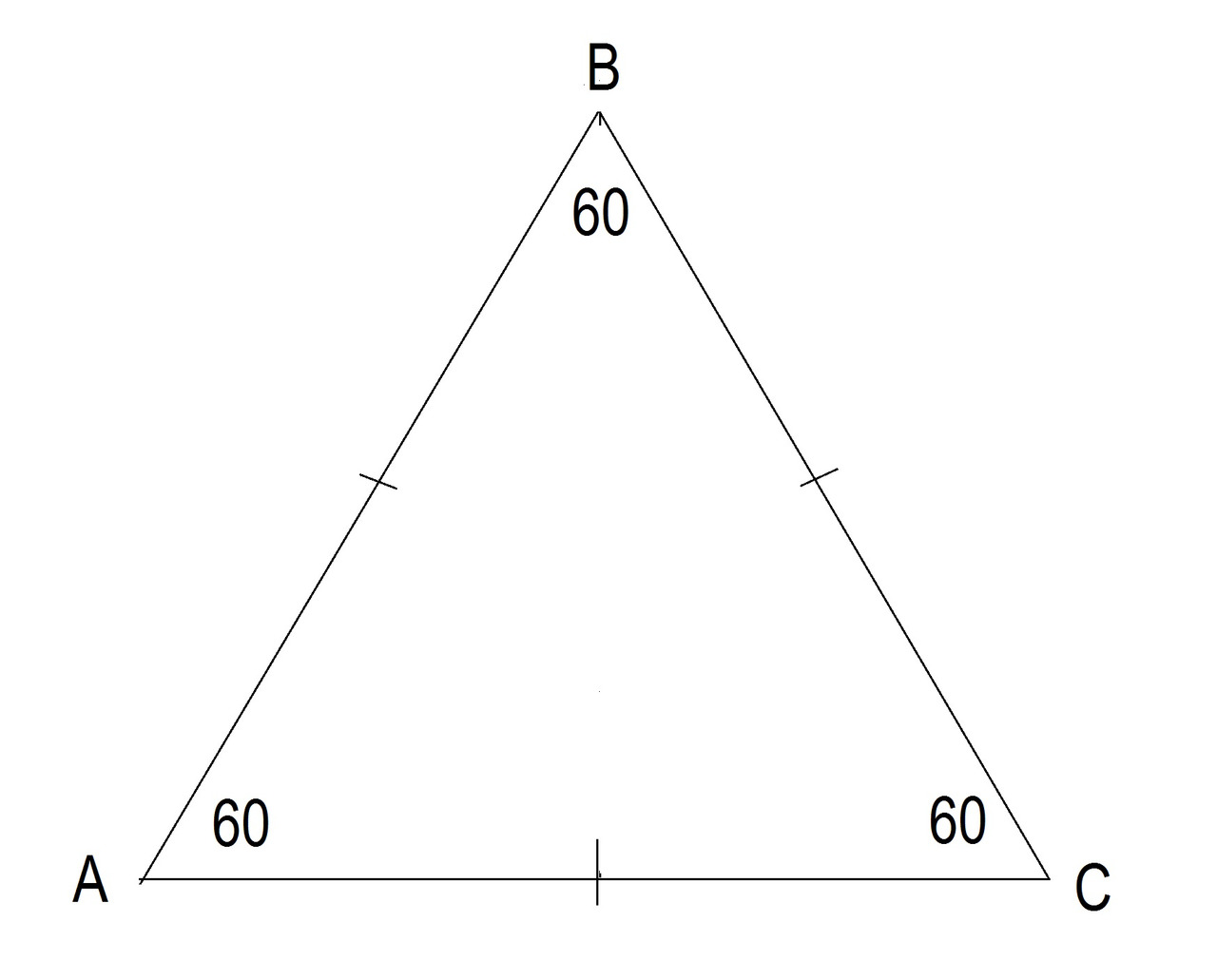
AB = BC = AC