
Предисловие
Эти таблицы я придумал для своих детей, которых учил сам, переведя их на семейную форму обучения.
Этот «учебник» состоит из таблиц и пояснений к ним. Считаю, так нагляднее и проще. Один французский математик изложил геометрию без единого чертежа. Но хотя его книга и была переведена на русский язык, уверен, ни один учитель математики ее не прочел, не говоря об учениках. Поэтому первая моя мысль была: изложить геометрию одними чертежами, без текста. Но в дальнейшем я пришел к выводу, что экстремизм тут не уместен.
Когда я закончил таблицы, я отнес их в существовавшую тогда еще газету «Первое сентября». Ведающая математическим разделом газеты полистала и сказала, что это нужно опубликовать в разделе для вспомогательных школ. «Но как же так, — возмутился я, — тут же полные доказательства всех теорем!» Она ответила, что мой «учебник» для обычных школьников СЛИШКОМ ПРОСТОЙ, а нужно воспитывать в детях трудолюбие. Вот так.
Но я так не считаю. Вполне возможно, для развития трудолюбия стоило бы увеличить программный материал, но пока этого МО не делает, наоборот — постоянно ведутся дискуссии о колоссальной перегрузке детей. Так что я предлагаю обычным школьникам свой простейший «учебник», чтобы они не слишком страдали и все-таки полюбили этот прекрасный школьный предмет — геометрию.
Конечно, этой книжечки недостаточно для изучения геометрии, но учебник будет понятнее, а итоговое повторение проще.
Автор.
Прямые и окружности. Точки пересечения. Аксиомы
Прямые и точки — это основные понятия геометрии, которым не даются определений. Считается, что и так понятно, что это такое.
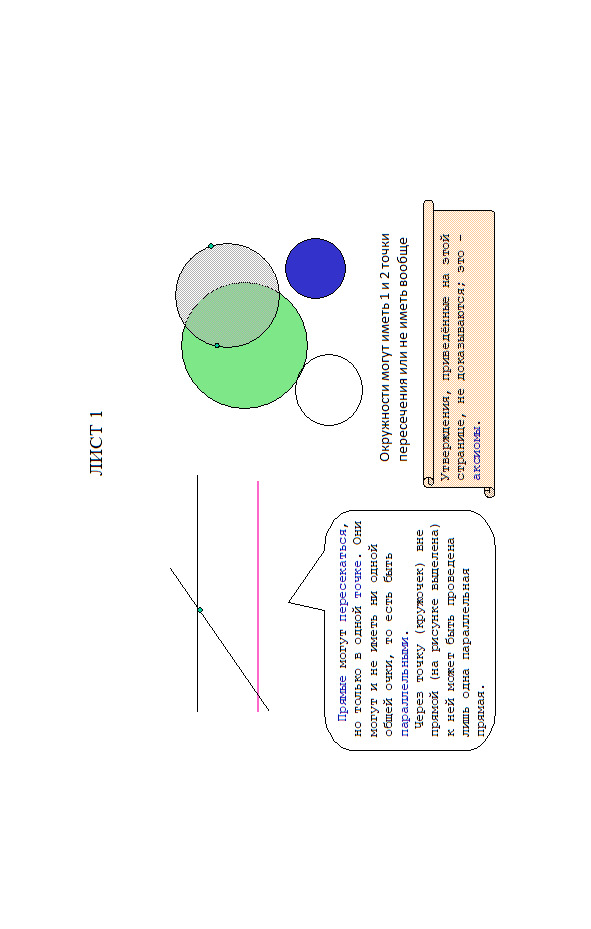
Прямые, подобно всем другим геометрическим фигурам, состоят из точек, то есть являются множеством точек. Если две прямые имеют общую точку, то говорят, что прямые пересекаются в этой точке. Если прямые не имеют общих точек, то они называются параллельными. Внимание! Через точку вне прямой можно провести не более одной параллельной к ней. (Запомните).
Окружности состоят из точек, расположенных на одном и том же расстоянии от центра окружности. Если две окружности имеют общие точки (одну или две), говорят, что они пересекаются в этих точках.
Аксиомы — это изначальные простые утверждения, с которых начинается изложение геометрии. Аксиомы не доказываются, считается, что их правильности доверяют, в отличие от теорем — остальных утверждений геометрии, которые всегда требуют доказательства.
В разных учебниках приняты разные наборы аксиом. Мы будем считать аксиомами, что различающиеся прямые могут пересекаться не более, чем в одной точке, а окружности разного радиуса — не более, чем в двух.
Плоскость. Равенство фигур. Симметрия
Понятие плоскость также не определяется и считается основным и изначально ясным. Любую фигуру можно двигать по плоскости, не меняя ее размеров, и переворачивать.
Две фигуры считаются равными, если при этом одну из них можно наложить на другую так, чтобы они совпали.
Так как плоскость — это множество точек, то она считается фигурой, поэтому ее можно двигать саму по себе и переворачивать.
Если согнуть плоскость (то есть лист чертежа) с нарисованной на ней фигурой, то эта фигура «отпечатается» с другой стороны линии сгиба. Тогда эти фигуры называются симметричными (или зеркально-симметричными) друг другу. Линия сгиба называется осью симметрии. Вы можете поэспериментировать на эту тему с кляксами, но я не советую.
Точка — тоже фигура (множество, состоящее из одного элемента). Каждая точка имеет симметричную себе относительно данной оси симметрии. Фигура, симметричная данной, состоит из всех точек, симметричных точкам данной фигуры.
Две точки выделяют на прямой отрезок — множество точек между ними. Две эти точки зазываются концами отрезка.

Вертикальные углы. Внутренние накрест лежащие углы
Любая точка прямой разбивает ее на два луча. Сама же эта точка называется их вершиной. Два луча с общей вершиной (не обязательно на одной прямой) называются углом. Лучи при этом называются сторонами угла. Если стороны одного угла — продолжения сторон второго, то углы называются вертикальными. Они равны друг другу. Для доказательства углы поворачивают на 180о и они совпадают.
Прямая, пересекающая пару (не обязательно параллельных) прямых, называется секущей. Пара углов, стороны которых содержат отрезок секущей между прямыми, вторые стороны которых лежат по разную сторону от нее (в общем — как на рисунке!), называются внутренними накрест лежащими. Если прямые параллельны, то внутренние накрест лежащие углы равны. Если внутренние накрест лежащие углы равны, то прямые параллельны.
Две эти теоремы построены принципу: 1) А следовательно В, 2) В следовательно А. Такие теоремы называются взаимно-обратными.
Доказательство обратной теоремы в нашем случае (для знатоков). Если углы не равны, проведем через одну из вершин углов прямую, которая давала бы равный угол. Тогда она была бы второй прямой, проходящей через вершину этого угла, притом обе были бы параллельными другой прямой (одна по условию, вторая — по прямой теореме). А это невозможно (помните?!).
Бесплатный фрагмент закончился.
Купите книгу, чтобы продолжить чтение.