Бесплатный фрагмент - Элементы теории множеств и математической логики.

1.Элементы теории множеств и математической логики

1.1.Понятие множества. Отношения между множествами

Понятие множества является одним из основных понятий математики.

Можно сказать, что множество — это совокупность некоторых объектов, объединенных по какому-то определенному признаку.

Приведем примеры, поясняющие содержание понятия множества:

— множество строк на этой странице;

— множество домов на данной улице;

— множество целых чисел;

— множество студентов в аудитории.

Объекты или предметы, составляющие данное множество, называются его элементами. Множество как бы объединяет многое в единое.

Множество можно описать одним из следующих способов:

— в виде списка или таблицы: все элементы множества непосредственно перечисляются. Этот способ удобен, если множество невелико (смотрите примеры 1 и 4);

— указанием способа конструирования множества, когда задается определенное правило, выражаемое словами или формулами, в соответствии с которыми можно сказать, принадлежит данный объект к рассматриваемому множеству или нет (примеры 2 и 3).

Для обозначения множеств обычно используют прописные буквы А,В,Х,У и т.д, а элементы соответствующего множества обозначают буквами а, в, х,у и т. д.

В том случае, когда х является элементом множества А, пишут так: А = {x}.

Запись А = {x: P} означает множество всех х, удовлетворяющих условию Р.

Пример 1.

Запись А = {1,2,5,7} означает, что множество А состоит из четырех элементов 1,2,5,7.

Пример 2.

Х = {х: х является студентом, рост которого больше 170 сантиметров}. Это множество описано способом конструирования.

Пример 3.

А= {у: у> 3} означает множество всех чисел, больших трех. Описано методом правила.

Пример 4.

Запись А= {а,б,м,н,и,ю,ч} означает, что множество А состоит из семи элементов а,б,м,н,и,ю,ч, которые являются буквами русского алфавита.

К сожалению, в редакторе издательства. в списке специальных символов оказался только один специальный символ, который используется в теории множеств и данной книге. Это очень затруднило и замедлило работу над книгой. В связи с этим я принял решение в рамках данной книги использовать специальную таблицу, которая. может быть, не очень удобна для читателя, но позволяет решить эту поблему.

В этой таблице все реальные символы закодированы в тексте книги определенным числом звездочек (*) — от 1 до 6.

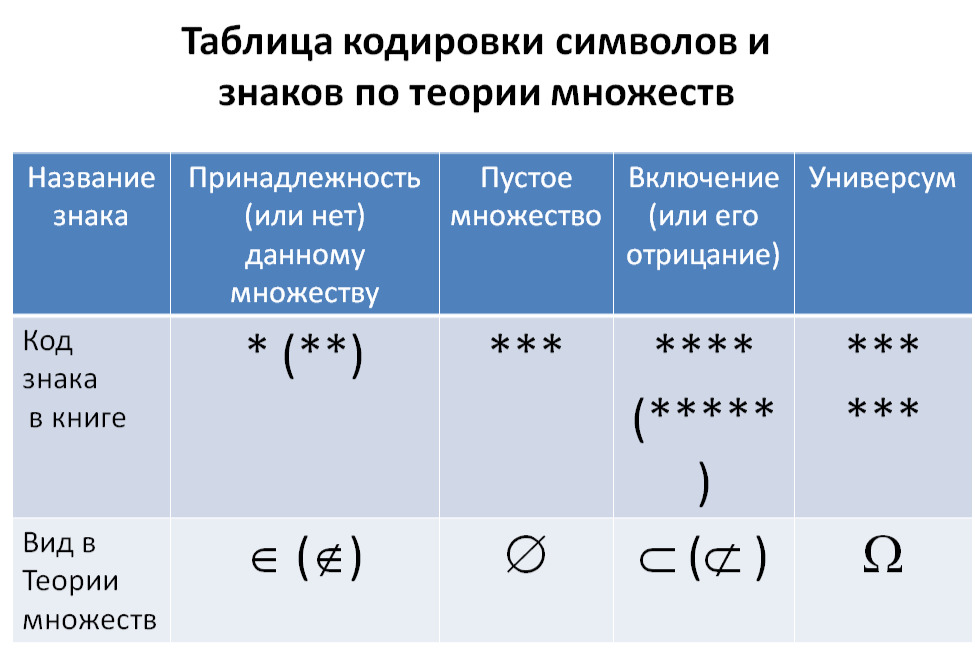
Если х является элементом множества А, то говорят, что х принадлежит А и записывают: х*А (x€A); если х множеству А не принадлежит, то пишут х **A (x перечеркнутый€ А).

Для того, чтобы выразить тот факт, что А — подмножество множества В, пользуются символом включения: А **** В. Это следует читать: « А содержится в В».

Отрицание включения обозначим символами — *****.

Так, например, если А есть множество четных чисел, то 2*A (2 € А), а число 5 (перечеркнутый€) А (не принадлежит), 5**A.

Подчеркнем, что каждый элемент может входить во множество только один раз.

Так, например, множество различных цифр числа 354577312 будет содержать только элементы 3,5,4,7,1,2.

Множества бывают конечными и бесконечными

Множество называется конечным, если оно содержит конечное число элементов (смотрите примеры 1 и 4), в противном случае оно является бесконечным (пример 3).

К конечным множествам относятся, в частности, одноэлементные множества, состоящие только из одного элемента. Необходимо различать объекты а и {а}:

а — один элемент некоторого множества, {а} — одноэлементное множество.

Если множество не имеет элементов, то его называют пустым

и мы обозначим его, в соответствии с таблицей, символами — ***.

Пример 5.

*** = {х: х — действительное число, квадрат которого равен -1}.

Пример 6.

*** = {х: х — лев, живущий на Луне}.

Необходимо различать следующие множества: *** {***}, {0}. Последние два множества не являются пустыми, т.к. каждое из них содержит по одному элементу. Второе служит примером множества, элемент которого, в свою очередь, представляет собой множество.

Множества могут находиться в различных отношениях между собой. Рассмотрим два из них: включение и равенство.

Определение 1.

Если каждый элемент множества А является также и элементом множества В, то множество А называется частью или подмножеством множества В.

Для того, чтобы выразить тот факт, что А — подмножество множества В, пользуются символом включения (****): А **** В. Это следует читать: « А содержится в В».

Отрицание включения (смотрите таблицу кодировки символов) обозначим символом — *****.

Отметим, что пустое множество *** и само множество В являются также подмножествами множества В, т.е. (***) **** В и В****В.

Пример 7.

А = {а,б,м,н,и,ю,ч} есть подмножество множества букв русского алфавита В = {а,б,в,…}.

Пример 8.

М = {{2,3}, {4,5,6}} — двухэлементное множество, элементами которого являются два других множества.

К = {{2,3}, {4,5,6},9,10,11} — пятиэлементное множество,

причем М *** К.

Пример 9.

L = {3,4, {3,4}} — трехэлементное множество, причем, 3*L и 4*L, но и {3,4} * L.

Определение 2.

Два множества А и В называются равными, если А* В и В *А.

Обозначается равенство множеств обычным способом: А = В. Из определения следует, что множества А и В равны тогда и только тогда, когда они состоят из одних и тех же элементов.

Пример 10.

{3,4,5,6} = {6,5,4,3}.

Пример 11.

{н,е,д,у.т,с} = {х: х- буква в слове «студент»}.

Равенство множеств (как и равенство чисел) удовлетворяет следующим свойствам:

1) рефлексивность: для всякого множества А  А = А.

2) транзитивность: для любых множеств А,В,С, если А = В и В = С, то и А = С.

3) симметричность: для любых двух множеств А и В, если А = В, то В = А.

2.Операции над множествами. Основные законы

Очень часто изучаемые в математике множества (чисел, точек, фигур, функций и т.д.) являются подмножествами некоторого множества, которое принимается за основное или универсальное (часто его называют «универсум»), и в рамках этой книги обозначается шестью символами — ******.

Сразу отметим, что «универсальное множество» — понятие относительное и всегда связано с определенной задачей или исследованием. Так, например, в геометрии на плоскости в качестве него следует рассматривать множество всех точек плоскости, а различные фигуры можно считать подмножествами. В арифметике универсальным множеством считается множество всех целых чисел и т. п.

Итак, множество всех элементов, относящихся к отдельной прикладной задаче, называется универсальным множеством. Рассматривая универсальное множество и его подмножество А, можно найти элементы из универсума, которые не принадлежат множеству А.

Определение 1.

Совокупность элементов, принадлежащих универсальному множеству ******, но не принадлежащих подмножеству А, называется дополнением подмножества А.

Обозначим его («не А»). Таким образом, «неA» = {х: х* (******), х ** А}.

С помощью диаграммы Эйлера-Венна можно представить универсальное множество в виде прямоугольника, а подмножество А — в виде круга, расположенного внутри этого прямоугольника.

Тогда, очевидно, что заштрихованная область будет

соответствовать дополнению (см. рис.1.1).

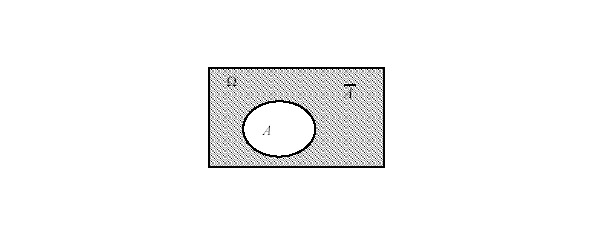
Замечание. Из определения дополнения множества А следует, что дополнение дополнения множества А есть множество А.

Над множествами можно проводить операции, во многом аналогичные арифметическим операциям.

Определение 2.

Объединением двух множеств А и В называется множество всех элементов, принадлежащих или множеству А, или множеству В, или им обоим сразу.

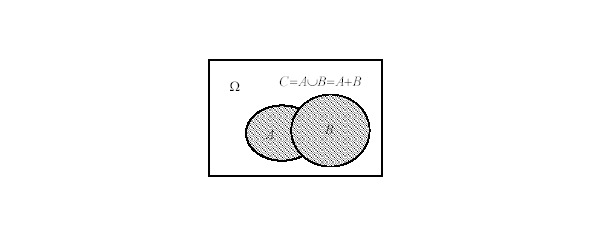
Объединение множеств обозначают разными символами («U"или «+»). В нашем случае: А + В = {х: х * А или х * В}.

Подчеркнем, что общие элементы входят в объединение только по одному разу.

Операцию объединения таких множеств иллюстрирует диаграмма Эйлера-Венна (см. рис.1.2). В качестве результата такой операции выступает множество С.

Пример 12.

Пусть А = {1,2,3,5} и В = {4,5,7,9}. Тогда А + В = {1,2,3,4,5,7,9}.

Пример 13.

Пусть Р = {х:-1 <= х <1},Q = {х:0 <х <1}. Тогда P+Q = {х:-1 <= х <1}. Или P+Q = Р.

Определение 3.

Пересечением двух множеств А и В называется множество всех элементов, принадлежащих и множеству А, и множеству В.

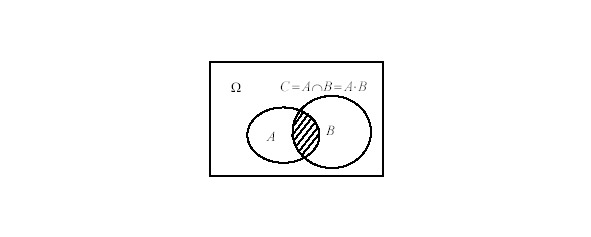
Пересечение множеств часто обозначают символом «подкова». Таким образом, в нашем случае: А (знак подковы) В = {х: х * А и х * В} (2).Часто эту операцию называют операцией пересечения множеств,

поэтому знак «x» здесь вполне уместен.

Иллюстрацией служит соответствующая диаграмма (см. рис.1.3). В качестве результата такой операции выступает множество С.

Пример 14.

Пусть А = {1,2,3,5} и В = {1,5,7,9}. Тогда А x В = {1,5}.

Если множества А и В не имеют общих элементов, то они называются непересекающимися.

Определение 4.

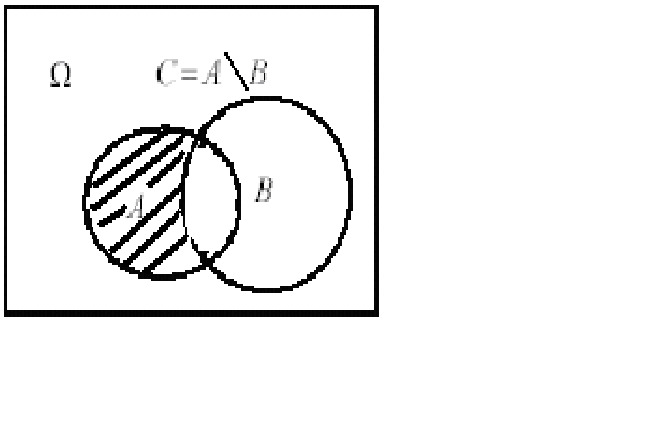
Разностью двух множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат множеству А, но не принадлежат множеству В. Разность множеств обозначают символом «\».

2.Что можно сказать о множестве В по отношению ко множеству А?

Таким образом, в нашем случае: А \ В = {х: х * А и х ** В} (3).

Операцию разности таких множеств иллюстрирует диаграмма Эйлера-Венна (см. рис.1.4). В качестве результата такой операции выступает множество С.

Пример 15.

Пусть А = {3,5,9,12} и В = {3,6,9,11}. Тогда А \ В = {5,12}.

Пример 16.

А = {х: 3 <= х <= 6},В = {х:0 <= х <= 4}.

Тогда А \ В = {х: 4 <= х <= 6}.

Для разности характерно:

1) (А \ В) x C = (А x C) \ (В x С).

2) А\А = ***.

3) ****** \А = «не A».

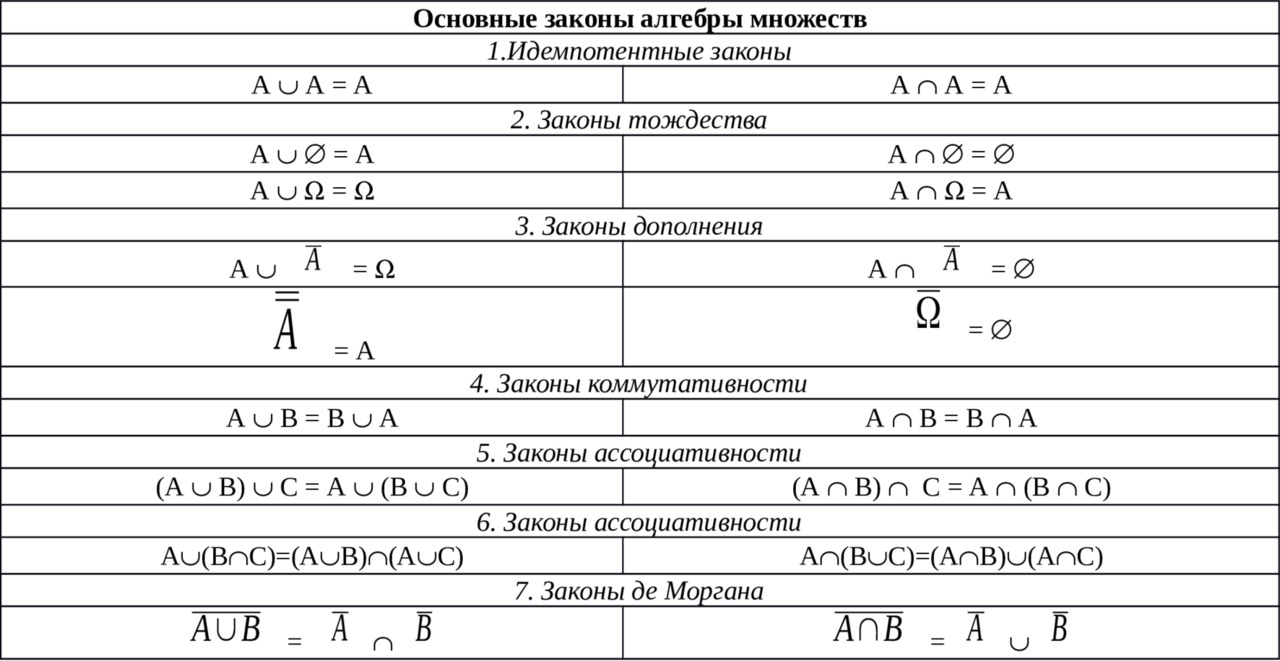
Операции над множествами (вместе со свойствами этих операций) образуют так называемую алгебру множеств, во многом аналогичную обычной алгебре. Естественно, что эта аналогия не полная.

Ниже, в виде таблицы, показаны основные законы алгебры множеств (Где: ****** — универсум, А,В,С — его любые подмножества)

3.Алгебра высказываний

АЛГЕБРА ВЫСКАЗЫВАНИЙ является составной частью одного из современных быстро развивающихся разделов математики — математической логики.

Математическая логика применяется в информатике, позволяет моделировать простейшие мыслительные процессы. Одним из занимательных приложений алгебры высказываний является решение логических задач.

Основными элементами математической логики служат так называемые высказывания или суждения.

Под высказыванием будем понимать любое утверждение или предложение, относительно которого можно сказать, что оно истинно (и) или, что оно ложно (л), и каждое из которых не может быть одновременно истинно или ложно. Высказывания будем обозначать прописными латинскими буквами.

Приведем примеры высказываний:

А — «Санкт-Петербург — культурная столица России» (и).

В — «Слон — большая рыба» (л).

С — «Снег черный» (л).

D — «5 <9» (и).

Е — «100 делится на 5» (и).

F — «10> 20» (л).

Если высказывание A истинно, то пишут A = 1, если ложно, то используют запись A = 0.

Следует помнить, что высказывание — это не то же самое, что предложение в разговорном языке. Предложение — чисто грамматическое понятие, а высказывание — понятие логическое.

Не каждое предложение может быть высказыванием.

Например, такие фразы как «Сегодня хорошая погода», «Подайте мне книгу», «Да здравствует 128 группа!» « x> 0» не являются высказываниями, поскольку об истинности или ложности того, что утверждается в этих предложениях, говорить нет смысла.

Чтобы предложение стало высказыванием, важно одно: оно должно допускать возможность однозначного толкования — истинно оно или ложно.

Различают высказывания простые (элементарные) и сложные (составные).

Повествовательное предложение, в котором говорится об одном-единственном событии, называется простым высказыванием. Приведенные выше высказывания A,B,C,D,E,F рассматриваются как элементарные — их нельзя разделить на более простые.

Если же такое деление допустимо, то такое высказывание называют сложным (составным). Из простых высказываний можно образовывать новые, сложные высказывания. Это осуществляется с помощью логических союзов (связок) таких, как «и», «или», «не», «если …,то…», «тогда и только тогда» и др.

В алгебре высказываний все суждения рассматриваются только с точки зрения их логического значения, а от их содержания отвлекаются. Предложения могут быть не связаны по смыслу, важна только истинность или ложность составных частей.

Например, предложение «Если 2х2=5, то внешний угол треугольника равен сумме двух внутренних, не смежных с ним» в контексте разговора выглядит полной бессмыслицей. В алгебре логики оно представляет собой высказывание, в котором первая часть ложь, а вторая — истина.

Над высказываниями можно производить «логические операции» или (что, то же самое), образовывать новые сложные высказывания с помощью некоторых логических союзов или знаков.

Основными операциями над высказываниями являются:

— отрицание;

— конъюнкция;

— дизъюнкция;

— имликация;

— эквиваленция.

Определение 1.

Отрицанием высказывания А называется такое высказывание, которое истинно, когда А ложно, и ложно, когда А истинно. Обозначим его («не А»).