Бесплатный фрагмент - Атака на восстановление квантового ключа

Исследования Атак квантового восстановления ключа

Абстрактный

Квантовая безопасность легких блочных шифров привлекает все больше внимания. Однако существующие квантовые атаки на легкие блочные шифры сосредоточены только на квантовом исчерпывающем поиске, в то время как квантовые атаки в сочетании с классическими методами криптоанализа изучены недостаточно. В этой статье мы изучим атаку квантового восстановления ключа на SIMON32 / 64 с использованием алгоритма квантового амплитудного усиления в модели Q1. Сначала я повторно проанализирую сложность квантовой схемы квантового исчерпывающего поиска на SIMON32 / 64. Я более точно оценю количество ворот Клиффорда и уменьшаем количество Т-ворот. Кроме того, T-образная и полная глубина уменьшены из-за наших незначительных изменений. Затем, используя в качестве отличителя четыре дифференциала, данные Бирюковым в FSE 2014, я проверю атаку восстановления квантового ключа на 19-раундовой SIMON32 / 64. Я рассматриваю две фазы атаки восстановления ключа как два экземпляра QAA по отдельности, а первый экземпляр QAA состоит из четырех экземпляров sub-QAA. Затем я проектирую квантовую схему этих двух экземпляров QAA и оцениваю соответствующую им сложность квантовой схемы. Я пришёл к выводу, что квантовая схема моей атаки с квантовым восстановлением ключа ниже, чем квантовый исчерпывающий поиск. Моя работа в первую очередь изучает квантовую специализированную атаку на SIMON32 / 64. И это первая работа по изучению сложности квантовых специализированных атак с точки зрения сложности квантовых схем, которая представляет собой более детальный анализ сложности квантовых специализированных атак. Я проектирую квантовую схему этих двух экземпляров QAA и оцениваю соответствующую им сложность квантовой схемы. Я пришёл к выводу, что квантовая схема моей атаки с квантовым восстановлением ключа ниже, чем квантовый исчерпывающий поиск. Моя работа в первую очередь изучает квантовую специализированную атаку на SIMON32 / 64. И это первая работа по изучению сложности квантовых специализированных атак с точки зрения сложности квантовых схем, которая представляет собой более детальный анализ сложности квантовых специализированных атак. мы проектируем квантовую схему этих двух экземпляров QAA и оцениваем соответствующую им сложность квантовой схемы. Я пришёл к выводу, что квантовая схема моей атаки с квантовым восстановлением ключа ниже, чем квантовый исчерпывающий поиск. Моя работа в первую очередь изучает квантовую специализированную атаку на SIMON32 / 64. И это первая работа по изучению сложности квантовых специализированных атак с точки зрения сложности квантовых схем, которая представляет собой более детальный анализ сложности квантовых специализированных атак.

Ключевые слова: Квантовый криптоанализ, Легкие блочные шифры, Квантовое усиление амплитуды, Дифференциальный криптоанализ, Атака восстановления ключа, SIMON32 / 64

Вступление

Развитие квантовых вычислений представляет угрозу для классических криптосистем. Алгоритм Шора (Shor1994 г.) может нарушить безопасность криптосистем с открытым ключом, основанных на целочисленной факторизации и дискретном логарифме, что приводит к постквантовой криптографии. Что касается симметричных криптосистем, до алгоритма Саймона (Simon1997 г.) применяется в квантовом криптоанализе, есть только алгоритм Гровера (Grover 1997 г.), что помогает получить квадратичное ускорение.

Квантовому криптоанализу блочных шифров в последние годы уделяется много внимания. Следуя представлениям о

Безопасность PRF в квантовых условиях, предложенная Zhandry et al. (Жандры2012 г.), в квантовом криптоанализе существуют две модели защиты от блочных шифров, которые Каплан и др. назвали моделью Q1 и моделью Q2. в (Kaplan et al.2016b).

Модель Q1: Злоумышленнику разрешено только выполнять классические онлайн-запросы и выполнять квантовые автономные вычисления.

Модель Q2: Злоумышленник может выполнять квантовые вычисления в автономном режиме и делать запросы квантовой суперпозиции в режиме онлайн. То есть злоумышленник может запросить оракулу в состоянии суперпозиции и получить состояние суперпозиции в качестве результата запроса.

Мы можем заметить, что модель Q1 более реалистична, чем модель Q2, по той причине, что оракул должен разрешить доступ к суперпозиции. Тем не менее, по-прежнему имеет смысл изучить модель Q2, чтобы подготовиться к будущему с высокоразвитой технологией квантовой связи.

Фактически, квантовый криптоанализ в модели Q2 существует уже давно. В 2010 году Кувакадо и Мори построили квантовый различитель на 3-круговой структуре Фейстеля (Kuwakado and Morii2010 г.) с использованием алгоритма Саймона в модели Q2. Затем они также восстановили ключ Even-Mansour, также используя алгоритм Саймона в 2012 году (Kuwakado and Morii2012 г.). На Crypto2016 Каплан и др. расширили результат в (Kuwakado and Morii2010 г.; 2012 г.) и применил алгоритм Саймона для атаки на ряд режимов шифрования и аутентифицированного шифрования, таких как CBC-MAC, PMAC, OCB (Kaplan et al. 2016a). В модели Q2 алгоритм Саймона может быть объединен с алгоритмом Гровера для применения в квантовом криптоанализе против блочных шифров. Леандер и Мэй (2017 г.) впервые использовал эту идею для атаки на FX-конструкцию в модели Q2. Вдохновленные этой работой, Донг и др. (2020a) дала атаку квантового восстановления ключа на полный цикл ГОСТ также в модели Q2. Кроме того, алгоритм Бернштейна-Вазарани (BV) (Bernstein and Vazirani1997 г.) также может быть применен в квантовом криптоанализе. Ли и Ян (2015 г.) предложил два метода выполнения квантового дифференциального криптоанализа на основе алгоритма BV. Затем Се и Ян расширили результат на Ли и Ян (2015 г.) и представить несколько новых методов атаки на блочные шифры с использованием алгоритма BV (Xie and Yang 2019 г.).

В модели Q1 кажется, что квантовый криптоанализ становится менее мощным. Самая тривиальная квантовая атака — это квантовый исчерпывающий поиск, который определяет общую безопасность блочных шифров в квантовой среде. Грассл и др. представляют квантовые схемы для реализации исчерпывающего поиска ключей на AES и оценки квантовых ресурсов в модели Q1 (Grassl et al.2016 г.). После этого есть также некоторые другие результаты, исследующие квантовую схему AES (Almazrooie et al.2018 г.; Jaques et al.2020 г.; Zou et al.2020 г.; Langenberg et al.2020 г.). Кроме того, существует множество попыток квантовых специализированных атак в сочетании с классическими методами криптоанализа, например дифференциальным и линейным криптоанализом (Kaplan et al.2016b), атаки встречей посередине (Хосоямада и Сасаки 2018 г.; Bonnetain et al.2019 г.) и рикошетные атаки (Хосоямада и Сасаки 2020 г.; Донг и др.2020b).

За последнее десятилетие исследованиям легковесных блочных шифров было уделено много внимания. Исследователи предложили несколько легких примитивов, чтобы назвать некоторые из них, SIMON (Beaulieu et al.2015 г.), SPECK (Beaulieu et al. 2015 г.), СКИННИ (Beierle et al. 2016 г.), НАСТОЯЩЕЕ (Богданов и др. 2007 г.). Чтобы подготовиться к будущему с крупномасштабными квантовыми компьютерами, необходимо изучить квантовую безопасность легких блочных шифров. Было предпринято несколько попыток изучить общие квантовые атаки на некоторые легкие блочные шифры (Anand et al.2020c; Jang et al.2020 г.; Ананд и др.2020b). В этой статье мы сосредоточимся на квантовой безопасности SIMON. Семейство алгоритмов SIMON (Beaulieu et al.2015 г.) — это легкий блочный шифр, предложенный NSA в 2013 году и обладающий выдающейся производительностью аппаратной реализации. В классической обстановке было много специализированных атак, направленных на SIMON. Однако в квантовой ситуации единственная квантовая атака на SIMON описана в Anand et al. (2020c), где Ананд и др. представить квантовую схему алгоритма Гровера на вариантах SIMON и дать соответствующую оценку квантовых ресурсов, которая является общей квантовой атакой. Для дальнейшего изучения квантовой безопасности SIMON нам необходимо изучить специальные квантовые атаки SIMON. Примечательно, что при измерении сложности атаки все существующие квантовые специализированные атаки изучали сложность шифрования, в то время как в нашем исследовании мы впервые использовали стоимость ресурсов квантовой схемы в качестве меры сложности.

Модель атаки Мы рассматриваем атаку выбранного открытого текста на SIMON32 / 64 в модели Q1, где злоумышленник может делать классические онлайн-запросы оракула шифрования и может выбирать пары случайных сообщений с входным дифференциалом x. Чтобы осуществить такую атаку, противнику необходимо осуществить трансформацию:

qq

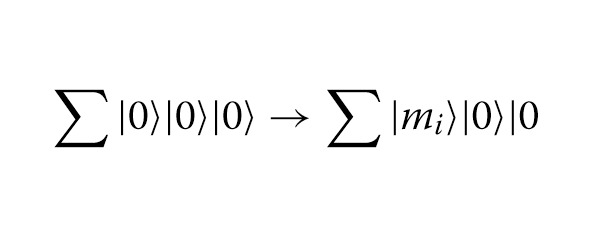
язнак равно1 я= 1

q

→ | mi |E |

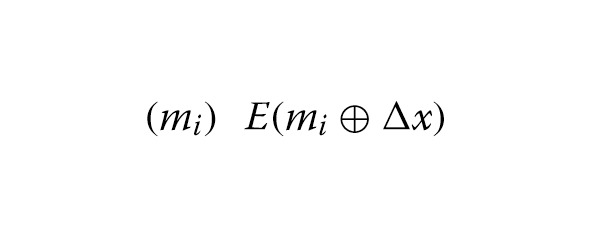
я= 1

когда задано q пар классической пары открытый текст-зашифрованный текст в качестве входных данных. Мы полагаем, что этот процесс эффективен. Таким образом, мы можем игнорировать стоимость квантовых ресурсов этого процесса.

Мой вклад В этой статье я изучаю атаку квантового восстановления ключа на SIMON32 / 64 с использованием квантового амплитудного усиления (QAA) в модели Q1. Наш вклад можно резюмировать в следующих двух аспектах.

— Я повторно анализирую сложность квантовой схемы квантового поиска мастер-ключа на SIMON32 / 64. С одной стороны, я далаю более точный результат оценки количества ворот Клиффорда и уменьшенного количества ворот Т. Я уменьшаю количество операций процесса расширения ключа, что снижает количество вентилей NOT и CNOT. Кроме того, подсчет ворот Клиффорда, разложенных по воротам Тоффоли, на общее количество ворот Клиффорда, помог мне дать более точную оценку количества ворот Клиффорда. И я уменьшаю количество Т-вентилей, используя декомпозицию мультиуправляемых вентилей НЕ на вспомогательные кубиты. С другой стороны, я даю более тщательный анализ глубины схем. Глубина, на которой я здесь обращаю внимание, — это глубина таких квантовых схем, которые состоят только из вентилей Клиффорда + Т. Вносим некоторые модификации в код реализации SIMON32 / 64, что уменьшает Tdepth и полную глубину контуров. По сравнению с (Анандом

и другие. 2020c), я даю более точный и тщательный анализ сложности квантовой схемы QMKS.

— Я представляю мою атаку с квантовым циклическим восстановлением ключа на SIMON32 / 64 с 19 этапами в сочетании с CRKR в

(Бирюков и др. 2014 г.). Я рассматриваю фазу частичного угадывания ключа и фазу исчерпывающего поиска как два экземпляра QAA по отдельности и проектируем соответствующую квантовую схему. Первый экземпляр QAA включает в себя четыре экземпляра суб-QAA, соответствующих четырем процессам восстановления ключа с использованием четырех дифференциалов. Затем оценим

сложность наших квантовых схем. Наконец, я сделаю простое сравнение между QMKS, QRKR и CRKR. Я пришол к выводу, что сложность шифрования самая низкая среди этих трех атак, а сложность квантовой схемы QRKR ниже, чем QMKS.

То есть я проводил квантовые специализированные атаки на 19round SIMON32 / 64, которые имеют меньшую сложность, чем универсальные квантовые атаки, как с точки зрения сложности шифрования, так и сложности квантовой схемы. В отличие от прежних квантовых специализированных атак, которые были сосредоточены только на сложности шифрования, моя работа делает первый шаг к изучению сложности квантовой схемы квантовых специализированных атак.

Контур Оставшаяся часть теста организована следующим образом. В «Предварительные мероприятия”Я вводу обозначения, используемые в этой статье, и базовые знания о блочном шифре SIMON, алгоритме QAA и квантовой схеме. В «Атака с исчерпывающим перебором по квантовому мастер-ключу на 19-раундовом SIMON32 / 64», Я повторно анализирую сложность квантовой схемы атаки квантового исчерпывающего перебора на SIMON32 / 64. В «Атака с квантовым циклическим ключом восстановления на SIMON32 / 64 с 19 раундами», Я описываю квантовую атаку с восстановлением ключа раунда на SIMON32 / 64 с 19 раундами. В «Анализ сложностиВ разделе я сравниваю сложность нашей атаки, квантовой атаки с поиском мастер-ключа и классической дифференциальной атаки. В «Заключение», Я делаю резюме этого документа.

Предварительные мероприятия

Обозначения

В этом разделе я перечисляю обозначения, используемые в этой статье, в таблице. 1.

Краткое описание SIMON

В этом разделе я кратко описываю SIMON. SIMON — это легкий блочный шифр со структурой Фейстеля. Существует множество вариантов SIMON для адаптации к различным вычислительным сценариям, различия между которыми заключаются в размере блока, размере ключа, размере слова и округлении. Размер блока SIMON составляет 2n бит, а размер ключа — mn бит. Мы могли бы использовать SIMON2n / mn для обозначения всех вариантов SIMON, где

Таблица 1 Обозначения

п ∈ {16, 24, 32, 48, 64} и m ∈ {2, 3, 4}. Все варианты SIMON приведены в таблице.2.

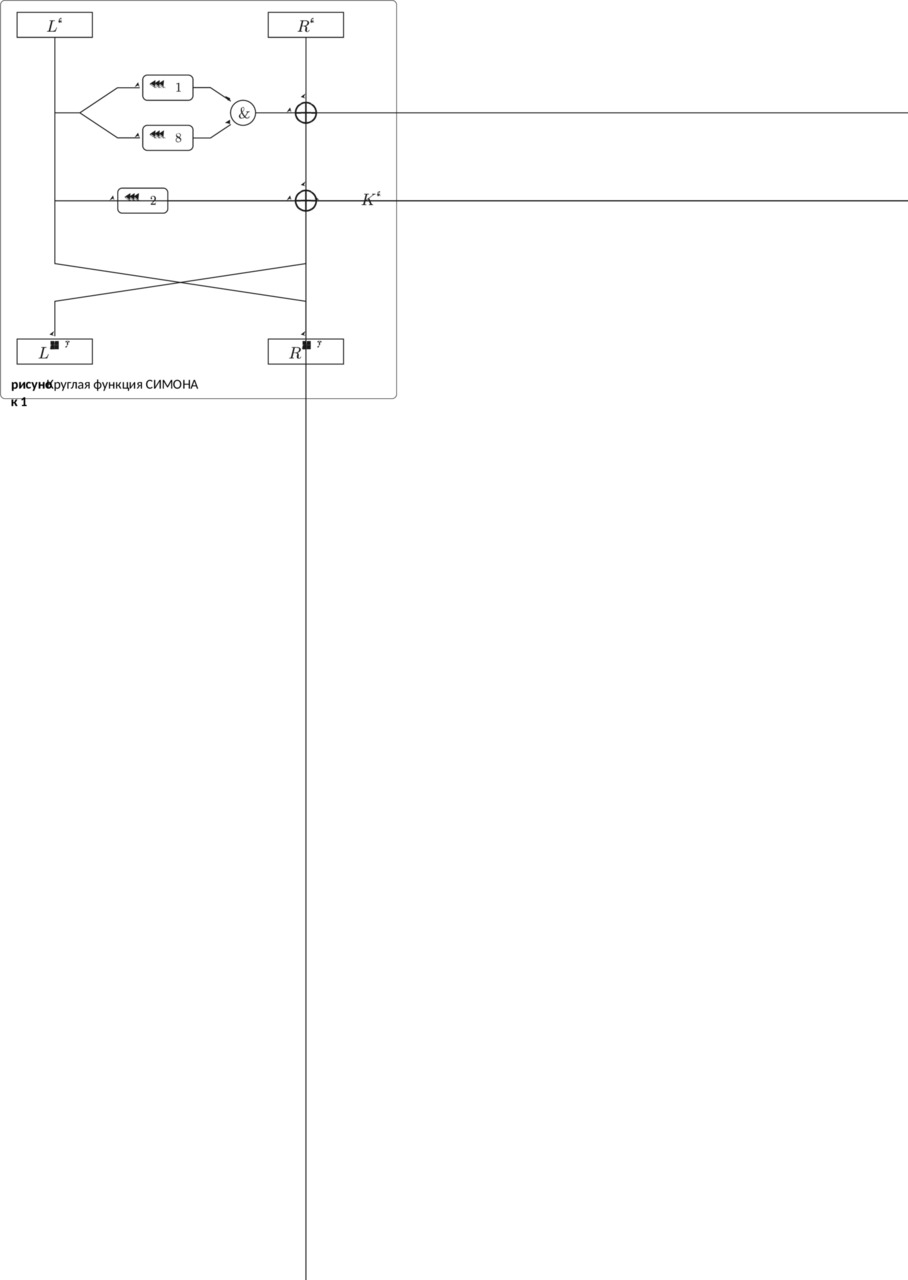
Круглая функция Структура i-й итерации SIMON2n / mn представлена на рис. 1. Мы легко можем видеть, что функция раунда SIMON2n / mn состоит из побитового AND, циклического поворота влево и побитового XOR. Для SIMON f: {0, 1} n → {0, 1} n определяется как f (x) = (x ≪ 1) & (x ≪ 8) ⊕ (x ≪ 2). Функция раунда определяется следующим образом:

F: {0, 1} n × {0, 1} n → {0, 1} 2n

F (Li +1, Ri +1) = (Ri ⊕ f (Li) ⊕ Ki, Li)

Ключевой график Для r-раунда SIMON2n / mn ключ раунда SIMON получается из первичного ключа {K0, K1, …, Km-1}. Конкретная схема расширения ключа определяется как:

— Когда i = 0, 1, …, m — 1, Ki = Ki;

— Когда i = m, m +1, …, r — 1,

Ki = c⊕ (zj) i — m⊕K (i — m) ⊕K (i — m +1) ⊕ (K (i — m +1) ≪

15) ⊕ (K (i — m +3) ≪ 13) ⊕ (K (i — m +3) ≪ 12);

zj — постоянная последовательность и c = 2n — 4. Ключевое расписание линейно. Таким образом, мы можем получить главный ключ из любых mn независимых битов подключей. В частности, для SIMON32 / 64, если мы получаем круглые ключи любых четырех соседних раундов, главный ключ может быть легко выведен.

Сопутствующие работы В классическом сеттинге уже были некоторые результаты атак на SIMON. Мы делаем простой обзор некоторых атак на SIMON32 / 64 в таблице.3. Однако в квантовой ситуации единственная квантовая атака на SIMON — это квантовый исчерпывающий поиск в Anand et al. (2020c). Для дальнейшего изучения квантовой безопасности блочного шифра SIMON мы изучаем в этой статье квантовую специализированную атаку на SIMON32 / 64. Согласно анализу в «Анализ сложности», я также перечисляю сложность квантовой универсальной атаки и нашей специальной квантовой атаки в Таблице 3 для сравнения.

Краткое описание алгоритма QAA

В этом разделе я кратко опишу алгоритм QAA. Алгоритм QAA является естественным обобщением алгоритма Гровера, который ищет все решения в несортированной базе данных. По сравнению с классическим алгоритмом, алгоритм QAA может достигать квадратичного ускорения. Согласно (Brassard et al.2002 г.), Алгоритм QAA можно резюмировать в следующей теореме.

Теорема 1. Позволять A — любой квантовый алгоритм, не использующий измерений, и пусть g: {0, 1} n → {0, 1} быть любым

Логическая функция. Пусть p будет начальной вероятностью успеха

А. Предположим, что p> 0 и положим m, куда sin2 (θ) = p. Определим G = UsUg = −AS0A — 1Ug, где S0 =

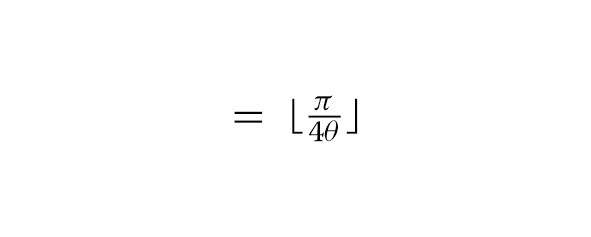
2 | 0 0 | −I. Если мы вычислим GmA | 0 и измерим систему, результат будет хорошим с вероятностью не менее max (1 — p, p).

Квантовая схема для алгоритма QAA представлена на рис. 2. Для простоты мы называем задачу поиска с использованием алгоритма QAA, чтобы урегулировать как экземпляр QAA. Каждая итерация экземпляра QAA называется итерацией QAA. Для экземпляра QAA с M решениями в N элементах мы определяем элементы, которые являются решениями, как ХОРОШИЕ, а элементы, которые не являются решениями, как ПЛОХОЕ. Определим функцию g: {0, 1} n → {0, 1} g (x) = 10, если, если xx ХОРОШО, это ПЛОХО

На основе функции g построим оракул Ug, который определяется как

Уг| x = | −x | x, если x — ПЛОХО, x — ХОРОШО

Процесс QAA описывается следующим образом: 1 Примените A к начальному состоянию | ψ = | 0, мы можем получить | ψ = A | 0 = | GOOD + | πBAD.

— Вызвать итерацию QAA m = 4θ раз. Каждая итерация состоит из двух шагов. Первый шаг — применить Ug к квантовому состоянию, после чего мы можем получить Ug | ψ = — | ХОРОШО + | ПЛОХО. Второй шаг — применить оператор диффузии 2 | s s| — от I до | ψ, где | s — равная суперпозиция всех элементов.

— Измерьте первый регистр и получите одно из всех решений.

Мы можем заметить, что по сравнению с исходным алгоритмом Гровера оператор H заменен случайным унитарным оператором A. Мы должны провести множество измерений, чтобы

получить все решения, потому что выходом алгоритма QAA является суперпозиция M решений.

Квантовая схема

В этом разделе я кратко познакомлю с соответствующими знаниями о квантовых схемах. Квантовые логические вентили являются основой квантовых схем. Квантовая схема может рассматриваться как последовательность квантовых логических вентилей. Чтобы измерить сложность квантовой схемы, мы должны учитывать количество вентилей, количество кубитов и глубину. При вычислении глубины квантовой схемы мы также принимаем допущение полного парреллизма, как в Jaques et al. (2020 г.), что означает, что квантовая схема может применять любое количество вентилей одновременно, пока эти вентили действуют на непересекающиеся наборы кубитов.

Набор вентилей Clifford + T представляет собой набор универсальных квантовых вентилей. Группа Клиффорда определяется как группа унитарных операторов, которые переводят группу операторов Паули в себя при сопряжении. Ворота Клиффорда затем определяются как элементы в группе Клиффорда. Основные ворота Клиффорда включают ворота H, S и CNOT. Однако мы не можем достичь универсальных квантовых вычислений только с вентилями Клиффорда. То есть в набор ворот нужно добавить не-Клиффордские ворота. И Т-вентиль обычно является выбором, который нужно добавить. Матричные представления Клиффорда + Т-вентиль, показанные в уравнении (1).

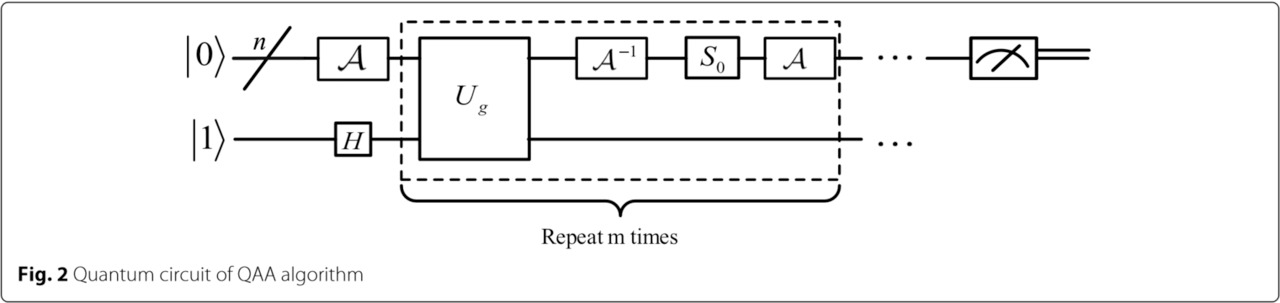
ЧАС,

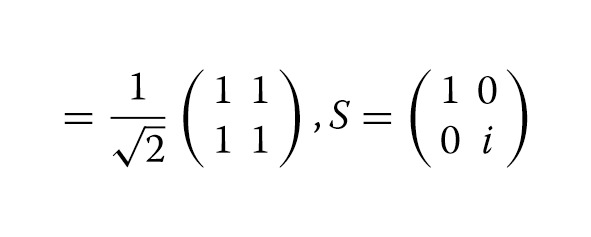
(1)

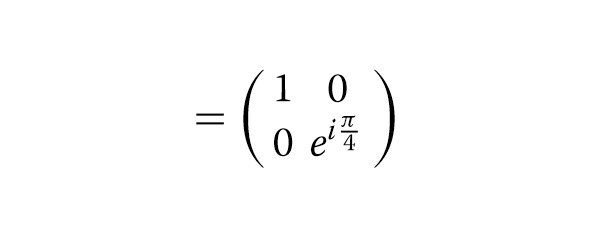
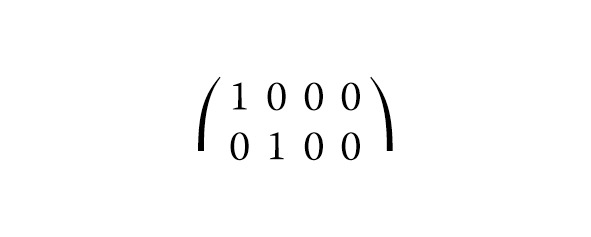
CNOT = ⎜⎜⎝ 0 0 0 10 0 1 0 ⎟⎟⎠, Т

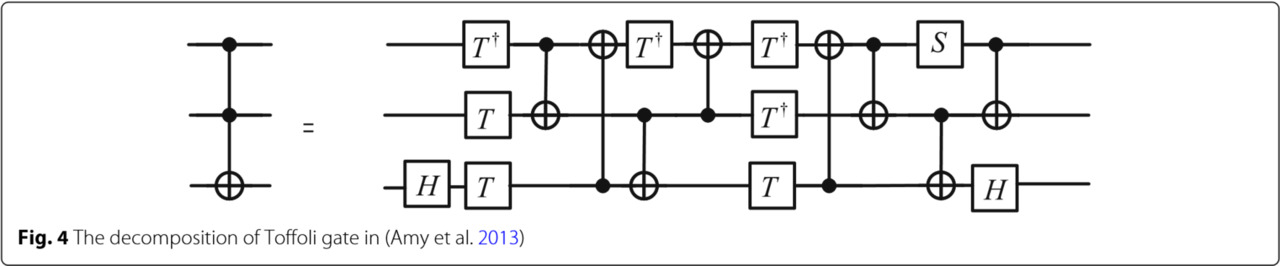
Согласно (Amy et al. 2013), все операции группы Клиффорда имеют трансверсальную реализацию и, следовательно, относительно просты в реализации, в то время как не-Клиффордовы ворота требуют для реализации гораздо более сложных и дорогостоящих методов. Поверхностные коды, которые обещают более высокие пороги, чем схемы конкатенированных кодов, также имеют значительно более сложную реализацию Т-образного элемента, чем любой из генераторов группы Клиффорда. В результате важно изучить количество Т-вентилей в квантовой схеме, чтобы измерить сложность квантовых вычислений. Кроме того, Эми и др. предложили T-глубину как функцию стоимости квантовых схем в Amy et al. (2013). Мы можем заметить, что исследованиям по уменьшению глубины T квантовых схем уделяется все больше и больше внимания. В классических вычислениях вентиль Тоффоли является универсальным классическим обратимым логическим вентилем, тогда как для квантовых вычислений его необходимо разложить на вентили Клиффорда + T для реальной реализации. Согласно (Нильсен и Чуанг2001 г.) разложение гейта Тоффоли показано на рис. 3.

То есть вентиль Тоффоли можно разложить на 7 вентилей T, 6 вентилей CNOT, 2 вентилей H и 1 вентиль S с T-глубиной 7 и полной глубиной 13. Затем, чтобы уменьшить T-глубину, Amy et al. предложил схему декомпозиции гейт Тоффоли в Amy et al. (2013) с Т-глубиной 3 и полной глубиной 10, показанной на рис. 4. И Эми и др. предположил, что эта T-глубина оптимальна для схем без вспомогательных компонентов. Хотя T-глубина может быть уменьшена до 1 с помощью вспомогательных кубитов в соответствии с рисунком 1 в Селингере (2013) количество вентилей CNOT значительно увеличивается. После общего рассмотрения количества вентилей и T-глубины квантовых схем я адаптирую метод, показанный на рис.4 чтобы разложить гейт Тоффоли в этой статье.

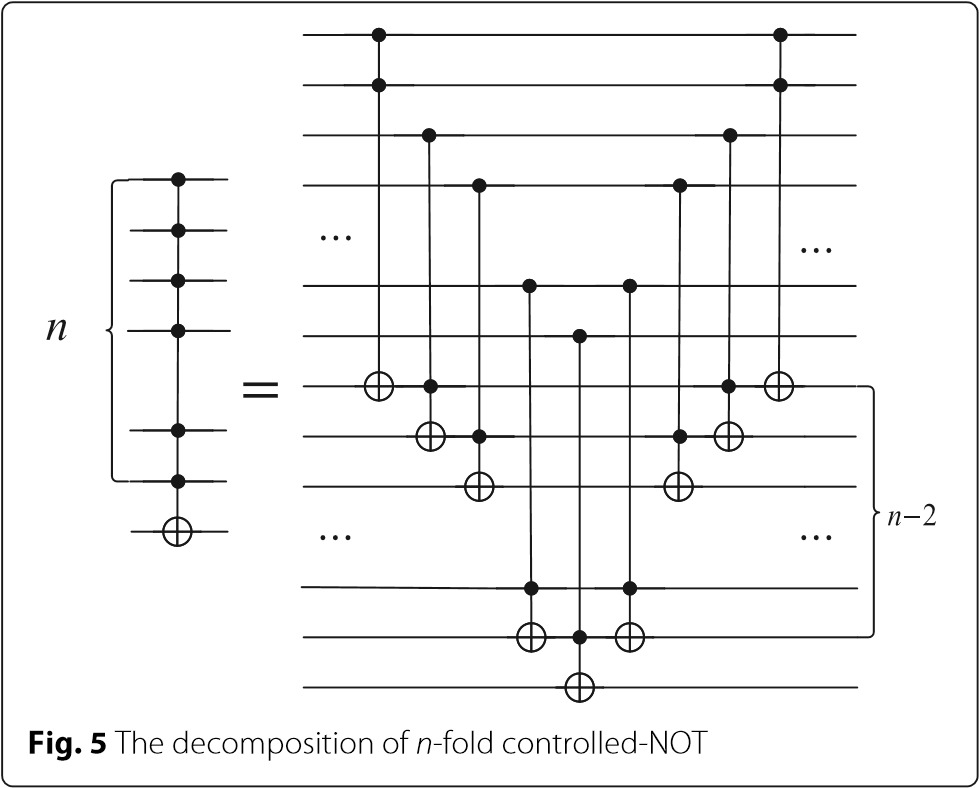
В итераторе G QAA есть два элемента с множественным управлением-НЕ. Для реальной реализации алгоритма QAA нам нужно разложить вентиль с дополнительным управлением-НЕ на серию вентилей Тоффоли. Затем нам нужно разложить ворота Тоффоли на ворота Клиффорд + T. Согласно (Нильсен и Чуанг2001 г.) n-кратное управляемое НЕ может быть разложено на 2n — 3 вентилей Тоффоли, используя n — 2 вспомогательных кубита. На рис.5. Здесь я предлагаю концепцию Toffoli-depth, которая похожа на T-depth, означающую количество ступеней в схеме, включающей вентили Тоффоли. В нашем анализе вычисление глубины Тоффоли является первым шагом к вычислению Tdepth и полной глубины квантовых схем. Мы можем заметить, что глубина Тоффоли на рис.5 равно 2n — 3. Таким образом, полная глубина реализации n-кратного управляемого НЕ составляет 20n-30, а T-глубина составляет 6n-9. Стоит отметить, что глубина, о которой я говорю, относится к глубине квантовых схем, содержащих только Клиффордские ворота и Т-образные ворота. То есть нам нужно разложить все вентили Тоффоли на вентили Клиффорда + T перед вычислением глубины квантовых схем.

Атака с исчерпывающим перебором по квантовому мастер-ключу на 19-раундовом SIMON32 / 64

В этом разделе, чтобы поставить эталон сравнения в одну и ту же шкалу, я повторно проанализирую сложность квантовой схемы QMKS с использованием алгоритма QAA, основанного на результатах, полученных Анандом и др. (2020c), где Ананд и др. представить алгоритм поиска Гровера на вариантах SIMON и оценить квантовые ресурсы для реализации такой атаки.

Сначала я представляю сложность квантовой схемы реализации 19-раундового SIMON32 / 64. Из таблицы 3 в Anand et al. (2020c), мы можем легко получить счетчик гейтов реализации 19-раундового SIMON32 / 64. Однако при вычислении глубины схемы мы получили разные результаты из (Anand et al.2020c). Ананд и др. реализовали все варианты SIMON в QISKIT (Koch et al.2019 г.). Глубину контура можно рассчитать с помощью функции Qiskit. После запуска кода реализации SIMON32 / 64, приведенного Анандом и др. (2020c) в Anand et al. (2020a), я обнаружил, что функция Qiskit вычисляет глубину квантовой схемы без декомпозиции элемента Тоффоли, что приводит к неполноте вычисления глубины схемы. По нашей оценке, вентили Тоффоли должны быть разложены на вентили Клиффорда + Т перед вычислением глубины схемы. Кроме того, я внёс небольшие изменения в код реализации SIMON32 / 64, которые привели к уменьшению полной глубины и T-глубины. Я сначала выполнил одну операцию со всеми битами, а затем выполнили следующую операцию со всеми битами, вместо того, чтобы выполнять все операции с каждым битом одну за другой в наших модификациях. Я предоставили мой модифицированный код в (Lau I2021 г.). Я перечисляю сложность квантовой схемы реализации SIMON32 / 64 в таблице.4.

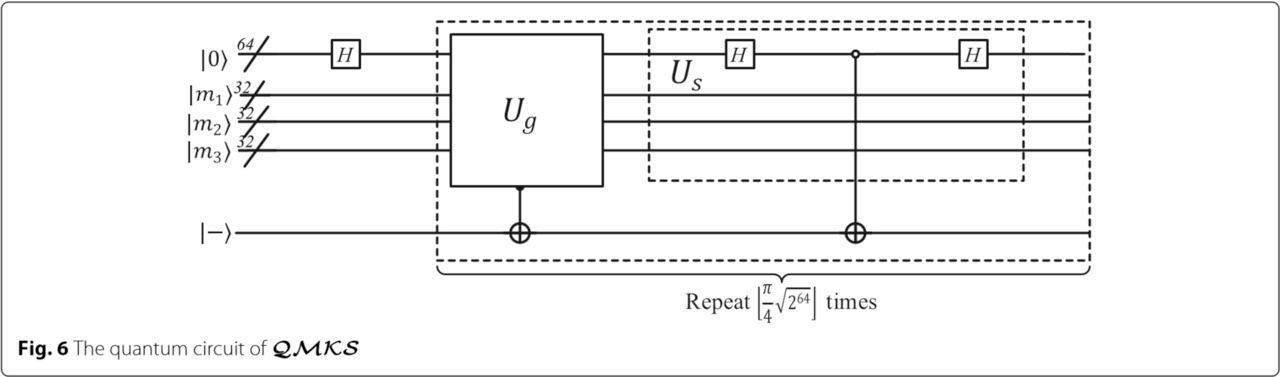
Затем я повторно анализирую сложность квантовой схемы квантовой схемы QMKS, показанной на рис. 6. Для реализации схемы на рис.6, нам необходимо реализовать итератор QAA G = UsUg. Реализация Ug представлена на рис.7, в котором выбраны 3 пары открытый текст-зашифрованный текст для однозначности решения. Оператор Us состоит из двух 64-кратных ворот Hardmard и одного 64-кратного регулируемого шлюза-НЕ. Здесь я повторно анализирую сложность квантовой схемы квантового исчерпывающего перебора на SIMON32 / 64 из следующих трех точек.

— Достаточно выполнить раскрытие ключа в Ug дважды, одно вычисление и одно невычисление. По оценке Ананда и др., Шесть ключевых процессов расширения для шести экземпляров SIMON были выполнены отдельно в Ug, что привело к завышению количества вентилей NOT и CNOT. Есть 448 ворот НЕ

и 1792 CNOT ворот во время ключевого процесса расширения. Легко вывести, что

# NOT = 448 × 2 = 896. Кроме того, ворота CNOT происходят из двух ключевых процессов расширения и

реализация шести экземпляров SIMON. То есть,

# CNOT = 28 × 64 × 2 +32 × 32 × 6 = 9728.

— При оценке ресурсов следует учитывать ворота Клиффорда, разложенные по воротам Тоффоли. Ананд и др. проигнорировал ворота Клиффорда, разложенные воротами Тоффоли. Вентили Тоффоли квантовой схемы на рис.6 происходят из реализации SIMON и разложения двух мультиуправляемых НЕ

Таблица 4 Стоимость SIMON32 / 64

ворота. В шести экземплярах SIMON имеется 512 × 6 = 3072 вентилей Тоффоли. Кроме того, согласно разложению гейта Тоффоли на рис.5, 96-кратный управляемый-НЕ вентиль в Ug и 64-кратный

вентиль с управляемым НЕ в Us может быть разложен на 2 × 96 — 3 +2 × 64 — 3 = 314 вентилей Тоффоли, используя не более 94 вспомогательных кубитов. Итак, мы имеем # Toff-C = (3072 +314) × 7 = 23702, # Toff-

H = (3072 +314) × 2 = 6772. Anand et al. принял результат (Roetteler and Wiebe2016 г.) для оценки количества Т-ворот, а я использую рис. 5 для оценки количества T-вентилей, что уменьшает количество T-вентилей за счет увеличения количества кубитов.

3 Результат оценки глубины схемы должен быть более подробным, а Т-глубина и полная глубина итератора QAA грамм можно было уменьшить. Я разлагаю два многоуправляемых логических элемента НЕ в операторе G на вентили Тоффоли, а затем разлагаем все вентили Тоффоли на вентили Клиффорда + T. Я рассматриваю глубину схемы этой схемы только с вентилями Клиффорд + T. Хотя в Ug шесть экземпляров SIMON, поскольку три экземпляра SIMON выполняются параллельно, нам нужно учитывать только глубину двух экземпляров SIMON. Однако я обнаружил, что Anand et al. посчитал глубину шести экземпляров SIMON в общую глубину G в Anand et al. (2020c), который завышает полную глубину и T-глубину G. Я оценил, что глубина Тоффоли итератора QAA G равна 96. Тогда я могу легко получить полную глубину и T-глубину G, как показано во второй строке Стол 4. Мы можем заметить, что моя оценка глубины меньше, чем результаты Anand et al. (2020c). Это связано с небольшими изменениями, которые мы внесли в схемную реализацию SIMON32 / 64. Кроме того, мы не проигнорировали глубину реализации двух вентилей НЕ с множественным управлением, что делает мою оценку более точной и полной.

С помощью приведенного выше анализа я представляю мои более точные результаты оценки итератора QAA G в таблице. 5. Чтобы найти главный ключ в ключевом пространстве {0, 1} 64, нам нужно повторить итератор QAA G = UsUg π4 232 раз. Из результата в таблице5, мы легко можем получить сложность квантовой схемы квантового исчерпывающего перебора на SIMON32 / 64 в таблице 6. По нашим оценкам, количество ворот Клиффорда немного выше, чем у Anand et al. (2020c), поскольку мы рассматриваем количество вентилей Клиффорда, разложенных на вентили Тоффоли. Кроме того, мы уменьшаем количество Т-вентилей, применяя декомпозицию мультиуправляемого НЕ-логического элемента, что также увеличивает количество кубитов. Также мы уменьшили T-глубину и полную глубину из-за небольших изменений в реализации SIMON32 / 64. Таким образом, моя оценка является более точной и подробной.